1 引言
在計算機算法設計中,使用遞歸技術往往使函數的定義和算法的描述簡捷且易於理解。有些數據結構如二叉樹等由於其本身固有的遞歸特性,特別適合用遞歸的形式來描述。還有一些問題,雖然其本身並沒有明顯的遞歸結構,但用遞歸技術來求解使設計出的算法簡潔、易懂。因此深入掌握遞歸技術在算法設計過程中可以設計出更加有效的算法[1]。
簡單地說,遞歸就是用自己定義自己。使用遞歸方法構造算法的基本思路是:當求解規模為n的問題時,先將其分解成若干個規模較小的與原問題具有相同特征的子問題,並找出子問題與原問題之間的組合關系,最後根據具體問題構造出遞歸算法。
遞歸算法的執行過程分“遞推”和“回歸”兩個階段。在遞推階段,把較復雜問題(如:規模為n)的求解推理至較原問題簡單一些的問題(如規模為n-1)的求解;在回歸階段,把遞推結束時所得到的解,逐級返回,依次得到稍復雜問題的解,最終得到原問題的解[2]。
Hanoi塔問題是一個典型的適合於利用遞歸技術得到簡潔算法的例子。Hanoi塔問題源自約19世紀末在歐洲出現的一種游戲,游戲中首先在一塊銅板上放置三根柱子,在第一根柱子上自上而下、由小到大順序串著64個盤子。游戲的目標是最後將所有盤子從第一根柱子上移到第三根柱子上,移動過程中可以用第二根柱子過渡。游戲規定一次只能移動一個盤子,並且任何時刻不允許大盤放在小盤的上面。
現在就給出關於Hanoi塔問題的程序,讓其將Hanoi塔問題的執行過程動態演示出來,以幫助讀者加深理解遞歸技術。
2 算法設計
我們先利用遞歸技術對該問題進行算法設計。我們將三根柱子分別標號為A、B、C,目標是要將n個盤子從A柱子移動到C柱子。該問題可以設計如下的遞歸算法:
第一步 將A柱子上n-1個盤子借助C柱子移動到B柱子上;
第二步 將A柱子上剩余的第n個盤子移動到C柱子上;
第三步 將B柱子上的n-1個盤子借助A柱子移動到C柱子上。
對於第一步和第三步,我們又可以利用類似的方法繼續將其求解過程設計為一個規模為n-1的Hanoi塔遞歸算法。
3 遞歸算法動態演示過程的程序實現
對於該算法的程序實現有兩個關鍵的難點,其一是初始化部分如何將三根柱子和n個盤子按照問題要求在屏幕上繪制出來;其二是盤子移動過程的圖形實現。
3.1 form窗體設計及程序初始化
首先在form窗體中添加三個命令按鈕,如圖1所示:
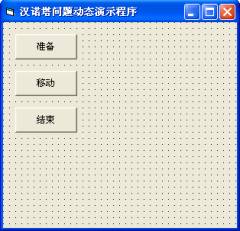
圖1 初始界面
在開始執行Hanoi塔問題求解過程之前,需要將三根柱子繪制在屏幕上,還需要接收用戶指定的盤子數及將盤子正確顯示至A柱子上。在本程序中接收盤子數是利用InputBox函數接收保存至全局變量number中,用實心矩形代表盤子。
這一部分的初始化工作在准備按鈕的click事件過程中實現,其核心代碼如下:
Dim i As Integer
'設置Form窗體屬性
Form1.Caption = "准備..."
Form1.Cls
'設置三個柱子的標記
CurrentX = 4000
CurrentY = hLevel + 61
Form1.FontSize = 16
Form1.ForeColor = vbRed
Form1.FontBold = True
Print "A"
CurrentX = 8000
CurrentY = hLevel + 61
Print "B"
CurrentX = 12000
CurrentY = hLevel + 61
Print "C"
Form1.ForeColor = &H80000012
Form1.FontSize = 10
Form1.FontBold = False
'畫底線
Form1.Line (0, hLevel)-(15360, hLevel + 100), vbGreen, BF
'畫三根柱子,A柱子的柱底坐標是(4000,10300)
'縱坐標減10只是為了顯示時看的效果更好一些,其實是不應該減的,減了後柱子底端縱坐標與底線上沿縱坐標就不一致了,但屏幕視覺是一致的
Form1.Line (3995, 700)-(4005, hLevel - 10), vbBlack, BF
Form1.Line (7995, 700)-(8005, hLevel - 10), vbBlack, BF
Form1.Line (11995, 700)-(12008, hLevel - 10), vbBlack, BF
number = Val(InputBox("請輸入盤子數:", "輸入數據", "3"))
Form1.Caption = "共有" & number & "個盤子"
'盤子寬400*i,高度200
'相鄰盤子之間的高度差設置為210,如果設置為相差200的話,當把上面一個盤子移走時兩個盤子重疊部分無法重新修復
For i = 1 To number
Form1.Line ((4000 - (i * 400) / 2), (hLevel - (number + 1 - i) * 210))-((4000 + (i * 400) / 2), (hLevel - (number - i) * 210 - 10)), , BF
Next i
baseCoordinateY(1) = hLevel - number * 210
baseCoordinateY(2) = hLevel
baseCoordinateY(3) = hLevel
3.2 盤子移動的實現
盤子的移動過程主要有兩種類型的移動,一種是垂直移動(包括自上而下和自下而上),另一種是水平移動(包括從左至右和從右至左)。盤子移動過程程序實現的主要思想是將每一次盤子從原位置移動到目標位置的路線分割成足夠多的子路徑,每個子路徑的距離足夠小,盤子從某子路徑一端移動至另一端通過兩個步驟來實現:第一步將原位置上的盤子顏色設置為form窗體背景色 Form1.
BackColor,以達到將盤子從原位置移開的顯示效果;第二步在盤子將要到達的新位置重新繪制該盤子,從而達到盤子移動到另一端的顯示效果。
例如某個用Form1.Line (4000, i)-( 4000 +400), i + 200)語句繪制的長為400像素、寬為200像素的盤子需要從矩形左上角坐標為(4000, i)的位置垂直向上移動到下一位置,則可能將該矩形在原位置重新繪制成窗體背景色,在矩形左上角坐標為(4000, i-stepC)位置重新繪制一個矩形來達到將該矩形從位置(4000, i)移動到位置(4000, i-stepC)的目的,其中stepC是移動步長,也即子路徑的長度。stepC值不能設置的過大,如果設置的太大,則盤子移動過程中將會出現不連續的移動效果。盤子移動過程程序實現的核心代碼如下:
Dim i As Integer, j As Integer, k As Integer 'i、k表示縱坐標,j表示橫坐標
Form1.Caption = "漢諾塔問題-第" & n & "個盤子正在移動..."
'向上移動到first柱子頂端
For i = baseCoordinateY(pillarnum(getone)) To 600 - 210 Step -stepC
'把矩形本次移動前的圖形擦掉
Form1.Line ((pillarnum(getone) * 4000 - (n * 400) / 2), i)-((pillarnum(getone) * 4000 + (n * 400) / 2), i + 200), Form1.BackColor, BF
fixpillar (getone)
Form1.Line ((pillarnum(getone) * 4000 - (n * 400) / 2), i - stepC)-((pillarnum(getone) * 4000 + (n * 400) / 2), i - stepC + 200), , BF
delay
Next i
'當前i =600-200-stepC,此時i值表示盤子的當前縱坐標
'向左、右平移到third柱子頂端
If pillarnum(getone) < pillarnum(putone) Then
'向右移
For j = (pillarnum(getone) * 4000 - (n * 400) / 2) To (pillarnum(putone) * 4000 - (n * 400) / 2) - stepC Step stepC
Form1.Line (j, i)-(j + n * 400, i + 200), Form1.BackColor, BF
Form1.Line (j + stepC, i)-(j + stepC + n * 400, i + 200), , BF
delay
Next j
Else
'向左移
For j = (pillarnum(getone) * 4000 - (n * 400) / 2) To (pillarnum(putone) * 4000 - (n * 400) / 2) + stepC Step -stepC
Form1.Line (j, i)-(j + n * 400, i + 200), Form1.BackColor, BF
Form1.Line (j - stepC, i)-(j - stepC + n * 400, i + 200), , BF
delay
Next j
End If
'向下移動到third柱子底端
For k = i To baseCoordinateY(pillarnum(putone)) - 210 - stepC Step stepC
'把矩形本次移動前的圖形擦掉
Form1.Line ((pillarnum(putone) * 4000 - (n * 400) / 2), k)-((pillarnum(putone) * 4000 + (n * 400) / 2), k + 200), Form1.BackColor, BF
fixpillar (putone)
Form1.Line ((pillarnum(putone) * 4000 - (n * 400) / 2), k + stepC)-((pillarnum(putone) * 4000 + (n * 400) / 2), k + stepC + 200), , BF
delay
Next k
'最後在柱子底端再補畫一次高度為210的矩形,
'因為k循環最後一次執行循環體時,k值未必正好等於循環終值baseCoordinateY(pillarnum(putone)) - 210 - stepC,
'所以要補一個上沿縱坐標為baseCoordinateY(pillarnum(putone)) - 210 - stepC矩形
Form1.Line ((pillarnum(putone) * 4000 - (n * 400) / 2), k)-((pillarnum(putone) * 4000 + (n * 400) / 2), k + 200), Form1.BackColor, BF
fixpillar (putone)
Form1.Line ((pillarnum(putone) * 4000 - (n * 400) / 2), baseCoordinateY(pillarnum(putone)) - 210)-((pillarnum(putone) * 4000 + (n * 400) / 2), baseCoordinateY(pillarnum(putone)) - 210 + 200), , BF
'更新各柱子最面一個盤子上沿的縱坐標
baseCoordinateY(pillarnum(getone)) = baseCoordinateY(pillarnum(getone)) + 210
baseCoordinateY(pillarnum(putone)) = baseCoordinateY(pillarnum(putone)) - 210
End Sub
Private Function pillarnum(ch As String) As Integer
pillarnum = Asc(ch) + 1 - Asc("A")
End Function
Private Sub fixpillar(pillarABC As String)
'縱坐標減10只是為了顯示時看的效果更好一些,其實是不應該減的,減了後柱子底端縱坐標與底線上沿縱坐標就不一致了
If pillarnum(pillarABC) < 3 Then
Form1.Line (pillarnum(pillarABC) * 4000 - 5, 700)-(pillarnum(pillarABC) * 4000 + 5, hLevel - 10), vbBlack, BF '修補柱子
Else
Form1.Line (pillarnum(pillarABC) * 4000 - 5, 700)-(pillarnum(pillarABC) * 4000 + 8, hLevel - 10), vbBlack, BF '修補柱子
End If
另外,需要注意的一點是當盤子垂直移動時,在盤子的原位置重新繪制盤子為窗體背景色時,由於會導致一段柱子也會被覆蓋成窗體背景色,因此在原位置繪制盤子為背景色之後應立即重新繪制一次柱子。
由於目前技術水平下PC機的CPU性能比較高,程序的執行時間非常短,為了得到一個適度緩慢的盤子移動速度,在盤子移動到下一個位置時應該暫停一個時間段。本程序中通過設置一個延遲函數以達到目的,當盤子從子路徑的一端移動到另一端時立即調用自定義延遲函數delay(),delay()函數只是起到暫停程序執行的作用,不執行任何改變盤子現狀的指令。一個delay()函數的例子如下:
Private Sub delay()
Dim tt As Double
tt = Timer
While Timer - tt < 0.001 '延遲
DoEvents
Wend
End Sub
4 結束語
本文實現了一個完整的Hanoi塔問題動態演示程序,由用戶輸入盤子數,盤子數目限定在1至10之間,盤子太多,屏幕顯示不下。程序編寫、運行環境為windows xp+vb6.0,屏幕分辯率為1024×768,程序運行界面如圖2所示。
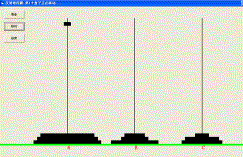
圖2 程序運行界面