在之前的文章中,給定一個顏色,它的色相值計算如下:
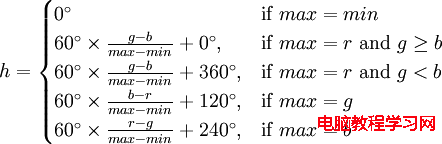
由公式可知,計算色相時要分為六種情況,計算略顯復雜。有沒有簡單的計算方法呢?來看看下面這個圖
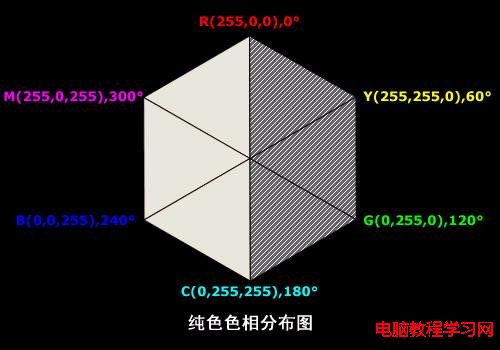
上面這個圖,表示純色的色相分布,把純色分為六個部分。仔細觀察,每個部分的純色都有統一的特點,例如,右上角的部分,R=255,B=0,G從0變化到255。右邊的部分,G=255,B=0,R從255變化到0。每一個部分都是一個分量是255,一個分量是0,一個分量在0到255之間變化。
在仔細觀察以後,突然發現,任意一種純色(R,G,B)和紅色之間的夾角可以用下面公式表示:
Θ=(|R-255|+|G-0|+|B-0|)/255×60
去掉絕對值符號後,簡化為
Θ=(255-R+G+B)/255×60
這時,Θ的取值范圍為 [0,180]。
再次觀察上面這個圖,發現右邊三個陰影部分的純色都有一個共性,那就是分量G的值大於等於分量B的值,而左邊三個空白部分的純色也都有一個共性,就是分量B的值大於等於分量G的值。
故任意一個純色的色相值可以用下面公式表示
當G≥B時,H=(255-R+G+B)/255×60
當G<B時,H=360-(255-R+G+B)/255×60
通過演化推導,任意一種顏色(R’,G’,B’)的色相計算公式:
Max為三個分量的最大值,Min為三個分量的最小值
若Max=Min,表示灰度色,此時,H=0
若Max≠Min,分為兩種情況:
當G≥B時,H=(Max-R’+G’-Min+B’-Min)/(Max-Min)×60
當G<B時,H=360-(Max-R’+G’-Min+B’-Min)/(Max-Min)×60
注:補充兩個公式,在後文中要用到的
純色(R,G,B),和紅色的夾角
Θ=(255-R+G+B)/255×60
和綠色的夾角
Θ=(255+R-G+B)/255×60
和藍色的夾角
Θ=(255+R+G-B)/255×60