二叉查找樹是滿足以下條件的二叉樹:
1、左子樹上的所有節點值均小於根節點值,
2、右子樹上的所有節點值均不小於根節點值,
3、左右子樹也滿足上述兩個條件。
二叉查找樹的插入過程如下:
1.若當前的二叉查找樹為空,則插入的元素為根節點,
2.若插入的元素值小於根節點值,則將元素插入到左子樹中,
3.若插入的元素值不小於根節點值,則將元素插入到右子樹中。
二叉查找樹的刪除,分三種情況進行處理:
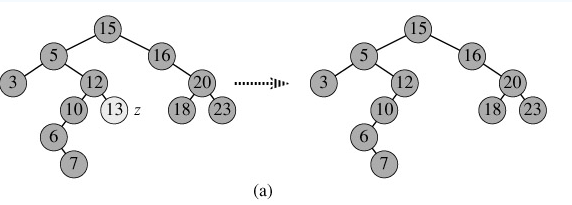
1.p為葉子節點,直接刪除該節點,再修改其父節點的指針(注意分是根節點和不是根節點),如圖a。
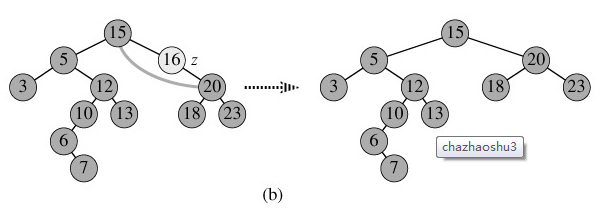
2.p為單支節點(即只有左子樹或右子樹)。讓p的子樹與p的父親節點相連,刪除p即可;(注意分是根節點和不是根節點);如圖b。
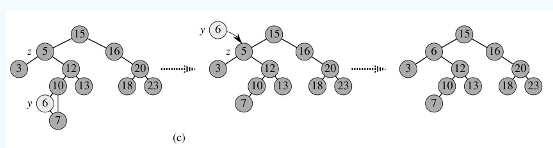
3.p的左子樹和右子樹均不空。找到p的後繼y,因為y一定沒有左子樹,所以可以刪除y,並讓y的父親節點成為y的右子樹的父親節點,並用y的值代替p的值;或者方法二是找到p的前驅x,x一定沒有右子樹,所以可以刪除x,並讓x的父親節點成為y的左子樹的父親節點。如圖c。
插入節點的代碼:
代碼如下:
struct node
{
int val;
pnode lchild;
pnode rchild;
};
pnode BT = NULL;
//遞歸方法插入節點
pnode insert(pnode root, int x)
{
pnode p = (pnode)malloc(LEN);
p->val = x;
p->lchild = NULL;
p->rchild = NULL;
if(root == NULL){
root = p;
}
else if(x < root->val){
root->lchild = insert(root->lchild, x);
}
else{
root->rchild = insert(root->rchild, x);
}
return root;
}
//非遞歸方法插入節點
void insert_BST(pnode q, int x)
{
pnode p = (pnode)malloc(LEN);
p->val = x;
p->lchild = NULL;
p->rchild = NULL;
if(q == NULL){
BT = p;
return ;
}
while(q->lchild != p && q->rchild != p){
if(x < q->val){
if(q->lchild){
q = q->lchild;
}
else{
q->lchild = p;
}
}
else{
if(q->rchild){
q = q->rchild;
}
else{
q->rchild = p;
}
}
}
return;
}
查找節點的代碼:
代碼如下:
pnode search_BST(pnode p, int x)
{
bool solve = false;
while(p && !solve){
if(x == p->val){
solve = true;
}
else if(x < p->val){
p = p->lchild;
}
else{
p = p->rchild;
}
}
if(p == NULL){
cout << "沒有找到" << x << endl;
}
return p;
}
刪除節點的代碼
代碼如下:
bool delete_BST(pnode p, int x) //返回一個標志,表示是否找到被刪元素
{
bool find = false;
pnode q;
p = BT;
while(p && !find){ //尋找被刪元素
if(x == p->val){ //找到被刪元素
find = true;
}
else if(x < p->val){ //沿左子樹找
q = p;
p = p->lchild;
}
else{ //沿右子樹找
q = p;
p = p->rchild;
}
}
if(p == NULL){ //沒找到
cout << "沒有找到" << x << endl;
}
if(p->lchild == NULL && p->rchild == NULL){ //p為葉子節點
if(p == BT){ //p為根節點
BT = NULL;
}
else if(q->lchild == p){
q->lchild = NULL;
}
else{
q->rchild = NULL;
}
free(p); //釋放節點p
}
else if(p->lchild == NULL || p->rchild == NULL){ //p為單支子樹
if(p == BT){ //p為根節點
if(p->lchild == NULL){
BT = p->rchild;
}
else{
BT = p->lchild;
}
}
else{
if(q->lchild == p && p->lchild){ //p是q的左子樹且p有左子樹
q->lchild = p->lchild; //將p的左子樹鏈接到q的左指針上
}
else if(q->lchild == p && p->rchild){
q->lchild = p->rchild;
}
else if(q->rchild == p && p->lchild){
q->rchild = p->lchild;
}
else{
q->rchild = p->rchild;
}
}
free(p);
}
else{ //p的左右子樹均不為空
pnode t = p;
pnode s = p->lchild; //從p的左子節點開始
while(s->rchild){ //找到p的前驅,即p左子樹中值最大的節點
t = s;
s = s->rchild;
}
p->val = s->val; //把節點s的值賦給p
if(t == p){
p->lchild = s->lchild;
}
else{
t->rchild = s->lchild;
}
free(s);
}
return find;
}