1、編寫程序,打印*菱形
推出第i行要打印的空白個數及*號個數,用for循環依次打印各行
代碼如下:
#include<stdio.h>
//總共要打印2*n-1行,逐行打印
void print1(int n)
{
int i,j;
for(i=1;i<=n;i++){//打印1至n行
for(j=1;j<=n-i;j++)//打印n-i個空格
printf(" ");
for(j=1;j<=2*i-1;j++)//打印2*i-1個*號
printf("*");
printf("\n");
}
for(;i<2*n;i++){//打印n+1至2*n-1行,同(2*n-i)行
for(j=1;j<=n-(2*n-i);j++)
printf(" ");
for(j=1;j<=2*(2*n-i)-1;j++)
printf("*");
printf("\n");
}
}
void main()
{
int n;//n是菱形邊上*號的個數
printf("enter n:");
scanf("%d",&n);
print1(n);
}
2、斐波納契數列(Fibonacci Sequence),又稱黃金分割數列,指的是這樣一個數列:
1、1、2、3、5、8、13、21、……在數學上,斐波納契數列以如下被以遞歸的方法定義:F(0)=0,F(1)=1,F(n)=F(n-1)+F(n-2)(n>=2,n∈N*).編寫程序,輸出F(20)的值。
這裡給出四種不同的解法,注意遞歸和改進的遞歸效率上有很大區別。
代碼如下:
#include<stdio.h>
#include<math.h>
#include<time.h>
#define MAX 100
//遞歸
int f1(int n)
{
if(n==1 || n==0)
return 1;
return f1(n-1)+f1(n-2);
}
//改進版的遞歸,去除重復計算
int f2(int n)
{
//保存中間結果的數組
static result[MAX]={1,1};
if(n==1 || n==0)
return 1;
if(result[n-1] == 0)
result[n-1]=f2(n-1);
if(result[n-2] == 0)
result[n-2]=f2(n-2);
return result[n-1]+result[n-2];
}
//用數組保存中間結果(來自陳孝傑)
int f3(int n)
{
int a[MAX],i;
a[1]=1;
a[0]=1;
for(i=2;i<=n;i++)
a[i]=a[i-1]+a[i-2];
return a[n];
}
//迭代
int f4(int n)
{
int i=2,a=1,b=1,sum=1;
while(i<=n){
sum=a+b;
a=b;
b=sum;
i++;
}
return sum;
}
void main()
{
long start,end;
start=clock();
printf("f(40)==%d\n",f1(40));
end=clock();
printf("用時:%d ms\n",end-start);
start=clock();
printf("f(40)==%d\n",f2(40));
end=clock();
printf("用時:%d ms\n",end-start);
start=clock();
printf("f(20)==%d\n",f3(20));
end=clock();
printf("用時:%d ms\n",end-start);
start=clock();
printf("f(20)==%d\n",f4(20));
end=clock();
printf("用時:%d ms\n",end-start);
}
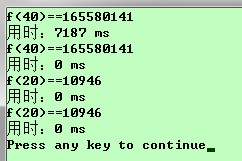
運行結果: