記得在學習數據結構的時候一味的想用代碼實現算法,重視的是寫出來的代碼有一個正確的輸入,然後有一個正確的輸出,那麼就很滿足了。從網上看了許多的代碼,看了之後貌似懂了,自己寫完之後也正確了,但是不久之後就忘了,因為大腦在回憶的時候,只依稀記得代碼中的部分,那麼的模糊,根本不能再次寫出正確的代碼,也許在第一次寫的時候是因為參考了別人的代碼,看過之後大腦可以進行短暫的高清晰記憶,於是欺騙了我,以為自己寫出來的,滿足了成就感。可是代碼是計算機識別的,而我們更喜歡文字,圖像。所以我們在學習算法的時候要注重算法的原理以及算法的分析,用文字,圖像表達出來,然後當需要用的時候再將文字轉換為代碼。記憶分為三個步驟:編碼,存儲和檢索,就以學習為例,先理解知識,再歸納知識,最後鞏固知識,為了以後的應用而方便檢索知識。
堆排序過程
堆分為大根堆和小根堆,是完全二叉樹。大根堆的要求是每個節點的值都不大於其父節點的值,即A[PARENT[i]] >= A[i]。在數組的非降序排序中,需要使用的就是大根堆,因為根據大根堆的要求可知,最大的值一定在堆頂。
既然是堆排序,自然需要先建立一個堆,而建堆的核心內容是調整堆,使二叉樹滿足堆的定義(每個節點的值都不大於其父節點的值)。調堆的過程應該從最後一個非葉子節點開始,假設有數組A = {1, 3, 4, 5, 7, 2, 6, 8, 0}。那麼調堆的過程如下圖,數組下標從0開始,A[3] = 5開始。分別與左孩子和右孩子比較大小,如果A[3]最大,則不用調整,否則和孩子中的值最大的一個交換位置,在圖1中是A[7] > A[3] > A[8],所以A[3]與A[7]對換,從圖1.1轉到圖1.2。
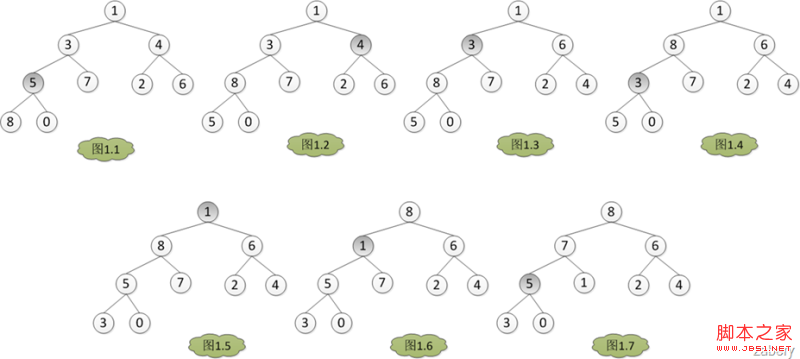
所以建堆的過程就是
代碼如下:
for ( i = headLen/2; i >= 0; i++)
do AdjustHeap(A, heapLen, i)
建堆完成之後,堆如圖1.7是個大根堆。將A[0] = 8 與 A[heapLen-1]交換,然後heapLen減一,如圖2.1,然後AdjustHeap(A, heapLen-1, 0),如圖2.2。如此交換堆的第一個元
素和堆的最後一個元素,然後堆的大小heapLen減一,對堆的大小為heapLen的堆進行調堆,如此循環,直到heapLen == 1時停止,最後得出結果如圖3。
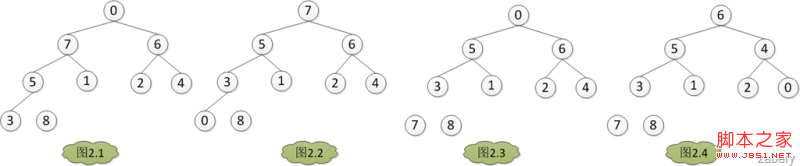
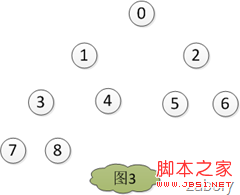
代碼如下:
/*
輸入:數組A,堆的長度hLen,以及需要調整的節點i
功能:調堆
*/
void AdjustHeap(int A[], int hLen, int i)
{
int left = LeftChild(i); //節點i的左孩子
int right = RightChild(i); //節點i的右孩子節點
int largest = i;
int temp;
while(left < hLen || right < hLen)
{
if (left < hLen && A[largest] < A[left])
{
largest = left;
}
if (right < hLen && A[largest] < A[right])
{
largest = right;
}
if (i != largest) //如果最大值不是父節點
{
temp = A[largest]; //交換父節點和和擁有最大值的子節點交換
A[largest] = A[i];
A[i] = temp;
i = largest; //新的父節點,以備迭代調堆
left = LeftChild(i); //新的子節點
right = RightChild(i);
}
else
{
break;
}
}
}
/*
輸入:數組A,堆的大小hLen
功能:建堆
*/
void BuildHeap(int A[], int hLen)
{
int i;
int begin = hLen/2 - 1; //最後一個非葉子節點
for (i = begin; i >= 0; i--)
{
AdjustHeap(A, hLen, i);
}
}
/*
輸入:數組A,待排序數組的大小aLen
功能:堆排序
*/
void HeapSort(int A[], int aLen)
{
int hLen = aLen;
int temp;
BuildHeap(A, hLen); //建堆
while (hLen > 1)
{
temp = A[hLen-1]; //交換堆的第一個元素和堆的最後一個元素
A[hLen-1] = A[0];
A[0] = temp;
hLen--; //堆的大小減一
AdjustHeap(A, hLen, 0); //調堆
}
}
性能分析
•調堆:上面已經分析了,調堆的運行時間為O(h)。
•建堆:每一層最多的節點個數為n1 = ceil(n/(2^(h+1))),

因此,建堆的運行時間是O(n)。
•循環調堆(代碼67-74),因為需要調堆的是堆頂元素,所以運行時間是O(h) = O(floor(logn))。所以循環調堆的運行時間為O(nlogn)。
總運行時間T(n) = O(nlogn) + O(n) = O(nlogn)。對於堆排序的最好情況與最壞情況的運行時間,因為最壞與最好的輸入都只是影響建堆的運行時間O(1)或者O(n),而在總體時間中占重要比例的是循環調堆的過程,即O(nlogn) + O(1) =O(nlogn) + O(n) = O(nlogn)。因此最好或者最壞情況下,堆排序的運行時間都是O(nlogn)。而且堆排序還是原地算法(in-place algorithm)。