接下來要了解的是遞增進位制、遞減進位制數和其序號的關系。遞增、遞減進位制數可以被看作一個有序的數字集合。如果規定遞增進位制和遞減進位制數的0的序號是十進制0,遞增進位制數的987654321和遞減進位制數的123456789對應十進制序號362880(即9!),則可以整理一套對應法則。其中,遞增進位制數(a1 a2 a3 a4 a5 a6 a7 a8 a9)為:
a1*9! + a2*8! + ….+ a8*2! + a9*1! = 序號
例如序號100的遞增進位制數就是4020,即4*4!+ 0*3!+ 2*2!+ 0*1!=100。將一個序號轉換成其遞增進位制數首先需要找到一個比序號小的最大階乘數(即1、2、6、24、120、720……),對其進行整數除得到遞增進位制的第一位;將除法的余數反復應用這個方法(當然,之後選擇的余數是小一級的階乘數),直到余數為0。
遞減進位制數(a1 a2 a3 a4 a5 a6 a7 a8 a9)為:
(((((((((a1 * 1 + a2) * 2 + a3) * 3 + …… + a7) * 8 + a8) * 9 + a9= 序號
例如序號100的遞減進位制數就是131(a7 a8 a9, 即從後對齊),即 (1*8 + 3)*9 + 1 = 100。將一個序號轉換成其遞減進位制數,需要對序號用9取余數,就可以得到遞減進位制的最末位(這點和遞增進位制先算出最高位相反)。用余下的數的整數除結果重復此過程(當然,依次對8、7、6……取余),直到余數為0。
關於遞增進位制和遞減進位制需要注意的重點:一是其加減法的進位需要小心;二是序號和數字的轉換。除了100之外,常見的轉換有:999的遞增數是121211,遞減數是1670;99的遞增數是4011,遞減數是130。大家可以以此為參考測試自己是否真正理解了計算的方法。下文將省略遞增進位制或遞減進位制的詳細計算過程。
從現在開始我們將詳細介紹六種排列生成算法。具體的理論介紹將被忽略,下文所注重的就是如何將排列映射為中介數以及如何將中介數還原為排列。
我全部以求839647521的下100個排列為例。
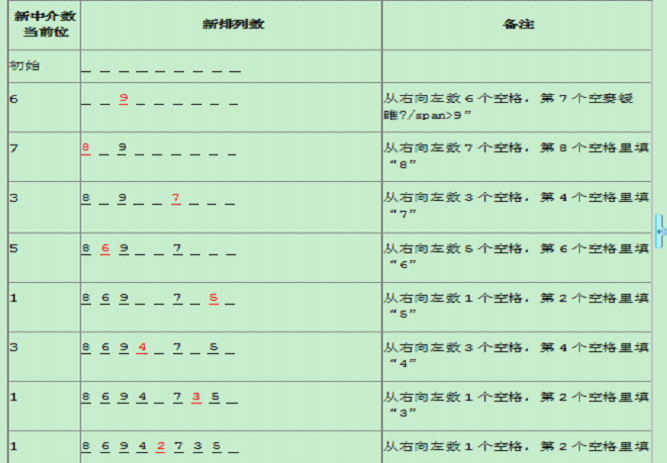
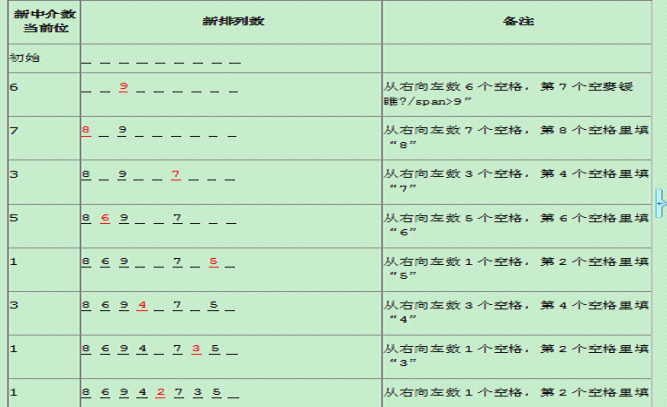
· 遞增進位排列生成算法還原方法:我們設新中介數的位置號從左向右依次是9、8、7、6、5、4、3、2。在還原前,畫9個空格。對於每一個在位置x的中介數y,從空格的右側向左數y個未被占用的空格。在第y+1個未占用的空格中填上數字x。重復這個過程直到中介數中所有的位都被數完。最後在余下的最後一個空格裡填上1,完成新排列的生成。以新中介數67351311為例,我給出了詳細的恢復步驟。其中紅色數字代表新填上的數字。最後得到新排列869427351。
 代碼如下:
代碼如下:還原方法:遞減進位制中介數的還原方法也剛好和遞增進位制中介數相反。遞增進位制還原方法是按照從中介數最高位(左側)到最低位(右側)的順序來填數。而遞減僅位置還原方法則從中介數的最低位向最高位進行依次計數填空。例如對於新中介數12224527,我給出了詳細的還原步驟。紅色代表當前正在填充的空格。最終得到新排列397645821。
C++實現代碼:
代碼如下:
void next_Permutations_by_DecreDecimal(int dataArr[],int size){
//創建一個結果數組,用來記錄下一個排列
int *resultArr = new int[size];
int i;
//第一步 求出中介數
map<int,int> agentMap;
for(i=0; i<size; ++i){
int nums = count(dataArr,i,size,dataArr[i]);
agentMap.insert(valType(dataArr[i],nums));
}
//第二步 求新的中介數 此處最低位進制最高,故不會頻繁產生進位,性能應該優於遞增進位
//最低位進制為9,向前依次遞減
int start = size,temp = 1;
int tmpResult;
int index = size-1;//中介數末位數位數字序列中最大的數右邊比其小的數
map<int,int>::iterator iter;
qsort(dataArr,0,size-1);
while (true){
++countNum; //全局變量 記錄排列個數
next_inter_num(dataArr,agentMap,size);
index = size -1;
//第三步 根據產生的中介數得到新的排列
for(i=0; i<size; ++i){
resultArr[i] = 0;
}
while(true){
iter = agentMap.find(dataArr[index]);
valType value = *iter;
//找到下一個填充空位
resultArr[getNextPosition(resultArr,size,value.second,0)] = dataArr[index];
--index;
if(index == 0) break;
}
i = 0;
while(true){
if(resultArr[i] != 0){
++i;
}else{
resultArr[i] = dataArr[index];
break;
}
}
print(resultArr,size);
bool flag = true;
for(i=1; i<size; ++i){
if(resultArr[i] > resultArr[i-1]){
flag = false;
break;
}
}
if(flag) break;
}
delete [] resultArr;
}
void next_inter_num(int dataArr[],map<int,int> &agentMap,int size){
int start = size,temp = 1;
int tmpResult;
int index = size-1;//中介數末位數位數字序列中最大的數右邊比其小的數
map<int,int>::iterator iter;
while(true){
iter = agentMap.find(dataArr[index]);
valType value = *iter;
tmpResult = value.second + temp;
if(tmpResult < start){
//沒有產生進位,直接改寫末位值
agentMap.erase(dataArr[index]);
agentMap.insert(valType(dataArr[index],tmpResult));
break;
}else{
//產生進位
agentMap.erase(dataArr[index]);
agentMap.insert(valType(dataArr[index],tmpResult % start));
tmpResult = tmpResult / start;
--start;
}
--index;
}
}
· 字典全排列生成法
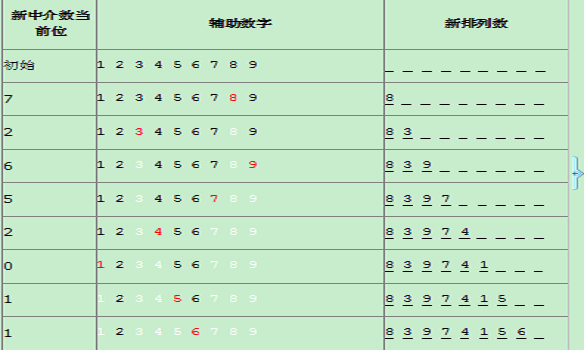
映射方法:將原排列數字從左到右(最末尾不用理會),依次查看數字右側比其小的數字有幾個,個數就是中介數的一位。例如,對於排列839647521。最高位8右側比8小的有7個數字,次高位3右側比3小的數字有2個,再次位的9的右側比9小的有6個數字,……,2的右側比2小的數有1個。得到遞增進制中介數72642321。(此中介數加上100的遞增進進制數4020後得到新中介數72652011)
還原方法:還原方法為映射方法的逆過程。你可以先寫出輔助數字1 2 3 4 5 6 7 8 9,以及9個空位用於填充新排列。然後從新中介數的最高位數起。例如新中介數最高位是x,你就可以從輔助數字的第一個沒有被使用的數字開始數起,數到x。第x+1個數字就應當是空位的第一個數字。我們將此數字標為“已用”,然後用其填充左起第一個空位。然後,再看新中介數的次高位y,從輔助數字的第一個未用數字數起,數到一。第y+1個數字就是下一個空位的數字。我們將此數字標為“已用”,然後用其填充左起第二個空位。依此類推,直到最後一個中介數中的數字被數完為止。例如對於新中介數72652011,我們給出其輔助數字和空位的每一步的情況。其中紅色的數字代表“正在標記為已用”,“已用”的數字不會再被算在之後的計數當中。當新中介數中所有的數字都被數完了,輔助數字中剩下的唯一數字將被填入最後的空位中。最終得到新排列839741562。