N皇後問題是一個經典的問題,在一個N*N的棋盤上放置N個皇後,每行一個並使其不能互相攻擊(同一行、同一列、同一斜線上的皇後都會自動攻擊)。
一、 求解N皇後問題是算法中回溯法應用的一個經典案例
回溯算法也叫試探法,它是一種系統地搜索問題的解的方法。回溯算法的基本思想是:從一條路往前走,能進則進,不能進則退回來,換一條路再試。
在現實中,有很多問題往往需要我們把其所有可能窮舉出來,然後從中找出滿足某種要求的可能或最優的情況,從而得到整個問題的解。回溯算法就是解決這種問題的“通用算法”,有“萬能算法”之稱。N皇後問題在N增大時就是這樣一個解空間很大的問題,所以比較適合用這種方法求解。這也是N皇後問題的傳統解法,很經典。
下面是算法的高級偽碼描述,這裡用一個N*N的矩陣來存儲棋盤:
1) 算法開始, 清空棋盤,當前行設為第一行,當前列設為第一列
2) 在當前行,當前列的位置上判斷是否滿足條件(即保證經過這一點的行,列與斜線上都沒有兩個皇後),若不滿足,跳到第4步
3) 在當前位置上滿足條件的情形:
在當前位置放一個皇後,若當前行是最後一行,記錄一個解;
若當前行不是最後一行,當前行設為下一行, 當前列設為當前行的第一個待測位置;
若當前行是最後一行,當前列不是最後一列,當前列設為下一列;
若當前行是最後一行,當前列是最後一列,回溯,即清空當前行及以下各行的棋盤,然後,當前行設為上一行,當前列設為當前行的下一個待測位置;
以上返回到第2步
4) 在當前位置上不滿足條件的情形:
若當前列不是最後一列,當前列設為下一列,返回到第2步;
若當前列是最後一列了,回溯,即,若當前行已經是第一行了,算法退出,否則,清空當前行及以下各行的棋盤,然後,當前行設為上一行,當前列設為當前行的下一個待測位置,返回到第2步;
算法的基本原理是上面這個樣子,但不同的是用的數據結構不同,檢查某個位置是否滿足條件的方法也不同。為了提高效率,有各種優化策略,如多線程,多分配內存表示棋盤等。
在具體解決該問題時,可以將其拆分為幾個小問題。首先就是在棋盤上如何判斷兩個皇後是否能夠相互攻擊,在最初接觸這個問題時,首先想到的方法就是把棋盤存儲為一個二維數組,然後在需要在第i行第j列放置皇後時,根據問題的描述,首先判斷是在第i行是否有皇後,由於每行只有一個皇後,這個判斷也可以省略,然後判斷第j列是否有皇後,這個也很簡單,最後需要判斷在同一斜線上是否有皇後,按照該方法需要判斷兩次,正對角線方向和負對角線方向,總體來說也不難。但是寫完之後,總感覺很笨,因為在N皇後問題中這個函數的使用次數太多了,而這樣做效率較差,個人感覺很不爽。上網查看了別人的實現之後大吃一驚,大牛們都是使用一個一維數組來存儲棋盤,在某個位置上是否有皇後可以相互攻擊的判斷也很簡單。具體細節如下:
把棋盤存儲為一個N維數組a[N],數組中第i個元素的值代表第i行的皇後位置,這樣便可以把問題的空間規模壓縮為一維O(N),在判斷是否沖突時也很簡單,首先每行只有一個皇後,且在數組中只占據一個元素的位置,行沖突就不存在了,其次是列沖突,判斷一下是否有a[i]與當前要放置皇後的列j相等即可。至於斜線沖突,通過觀察可以發現所有在斜線上沖突的皇後的位置都有規律即它們所在的行列互減的絕對值相等,即| row – i | = | col – a[i] | 。這樣某個位置是否可以放置皇後的問題已經解決。
下面要解決的是使用何種方法來找到所有的N皇後的解。上面說過該問題是回溯法的經典應用,所以可以使用回溯法來解決該問題,具體實現也有兩個途徑,遞歸和非遞歸。遞歸方法較為簡單,大致思想如下:
代碼如下:
void queen(int row)
{
if (n == row) //如果已經找到結果,則打印結果
print_result();
else {
for (k=0 to N) { //試探第row行每一個列
if (can_place(row, k) {
place(row, k); //放置皇後
queen(row + 1); //繼續探測下一行
}
}
}
}
該方法由於在探測第i行後,如果找到一個可以放置皇後的位置j後,則會遞歸探測下一行,結束後則會繼續探測i行j+1列,故可以找到所有的N皇後的解。
但是一般來說遞歸的效率比較差,下面重點討論一下該問題的非遞歸實現。
非遞歸方法的一個重要問題時何時回溯及如何回溯的問題。程序首先對N行中的每一行進行探測,尋找該行中可以放置皇後的位置,具體方法是對該行的每一列進行探測,看是否可以放置皇後,如果可以,則在該列放置一個皇後,然後繼續探測下一行的皇後位置。如果已經探測完所有的列都沒有找到可以放置皇後的列,此時就應該回溯,把上一行皇後的位置往後移一列,如果上一行皇後移動後也找不到位置,則繼續回溯直至某一行找到皇後的位置或回溯到第一行,如果第一行皇後也無法找到可以放置皇後的位置,則說明已經找到所有的解程序終止。如果該行已經是最後一行,則探測完該行後,如果找到放置皇後的位置,則說明找到一個結果,打印出來。但是此時並不能再此處結束程序,因為我們要找的是所有N皇後問題所有的解,此時應該清除該行的皇後,從當前放置皇後列數的下一列繼續探測。
完整的代碼如下:
代碼如下:
/**
* 回溯法解N皇後問題
* 使用一個一維數組表示皇後的位置
* 其中數組的下標表示皇後所在的行
* 數組元素的值表示皇後所在的列
* 這樣設計的棋盤,所有皇後必定不在同一行,於是行沖突就不存在了
* date : 2011-08-03
* author: liuzhiwei
**/
#include <stdio.h>
#include <stdlib.h>
#include <math.h>
#define QUEEN 8 //皇後的數目
#define INITIAL -10000 //棋盤的初始值
int a[QUEEN]; //一維數組表示棋盤
void init() //對棋盤進行初始化
{
int *p;
for (p = a; p < a + QUEEN; ++p)
{
*p = INITIAL;
}
}
int valid(int row, int col) //判斷第row行第col列是否可以放置皇後
{
int i;
for (i = 0; i < QUEEN; ++i) //對棋盤進行掃描
{
if (a[i] == col || abs(i - row) == abs(a[i] - col)) //判斷列沖突與斜線上的沖突
return 0;
}
return 1;
}
void print() //打印輸出N皇後的一組解
{
int i, j;
for (i = 0; i < QUEEN; ++i)
{
for (j = 0; j < QUEEN; ++j)
{
if (a[i] != j) //a[i]為初始值
printf("%c ", '.');
else //a[i]表示在第i行的第a[i]列可以放置皇後
printf("%c ", '#');
}
printf("\n");
}
for (i = 0; i < QUEEN; ++i)
printf("%d ", a[i]);
printf("\n");
printf("--------------------------------\n");
}
void queen() //N皇後程序
{
int n = 0;
int i = 0, j = 0;
while (i < QUEEN)
{
while (j < QUEEN) //對i行的每一列進行探測,看是否可以放置皇後
{
if(valid(i, j)) //該位置可以放置皇後
{
a[i] = j; //第i行放置皇後
j = 0; //第i行放置皇後以後,需要繼續探測下一行的皇後位置,所以此處將j清零,從下一行的第0列開始逐列探測
break;
}
else
{
++j; //繼續探測下一列
}
}
if(a[i] == INITIAL) //第i行沒有找到可以放置皇後的位置
{
if (i == 0) //回溯到第一行,仍然無法找到可以放置皇後的位置,則說明已經找到所有的解,程序終止
break;
else //沒有找到可以放置皇後的列,此時就應該回溯
{
--i;
j = a[i] + 1; //把上一行皇後的位置往後移一列
a[i] = INITIAL; //把上一行皇後的位置清除,重新探測
continue;
}
}
if (i == QUEEN - 1) //最後一行找到了一個皇後位置,說明找到一個結果,打印出來
{
printf("answer %d : \n", ++n);
print();
//不能在此處結束程序,因為我們要找的是N皇後問題的所有解,此時應該清除該行的皇後,從當前放置皇後列數的下一列繼續探測。
//_sleep(600);
j = a[i] + 1; //從最後一行放置皇後列數的下一列繼續探測
a[i] = INITIAL; //清除最後一行的皇後位置
continue;
}
++i; //繼續探測下一行的皇後位置
}
}
int main(void)
{
init();
queen();
system("pause");
return 0;
}
下面的代碼跟上面的代碼差不多,只是稍微做了一些變化。。上面函數判斷棋盤某個位置合法性的時候,valid函數裡面的QUEEN可以修改為row的,只需要將前面row行與第row行進行比較就可以了,不需要將所有行都與第row進行比較的。。。下面的代碼中的check函數中循環次數是k而不是皇後的個數就是這個原因。。。
代碼如下:
#include "iostream"
#include "cmath"
using namespace std;
#define Max 20 //定義棋盤的最大值
int a[Max];
int show(int S) //定義輸出函數
{
int i,p,q;
int b[Max][Max]={0}; //定義並初始化b[][]輸出數組
for(i=1;i<=S;i++) //按橫列i順序輸出a[i]數組坐標
{
b[i][a[i]]=1;
printf("(%d,%d)\t",i,a[i]);
}
printf("\n");
for(p=1;p<=S;p++) //按棋盤的橫列p順序標明皇後的位置
{
for(q=1;q<=S;q++)
{
if(b[p][q]==1) //在第p行第q列放置一個皇後棋子
printf("●");
else
printf("○");
}
printf("\n");
}
return 0;
}
int check(int k) //定義check函數
{
int i;
for(i=1;i<k;i++) //將第k行與前面的第1~~k-1行進行判斷
{
if((a[i]==a[k]) || (a[i]-a[k]==k-i) || (a[i]-a[k]==i-k)) //檢查是否有多個皇後在同一條直線上
{
return 0;
}
}
return 1;
}
void check_m(int num) //定義函數
{
int k=1,count=0;
printf("The possible configuration of N queens are:\n");
a[k]=1;
while(k>0)
{
if(k<=num && a[k]<=num) //從第k行第一列的位置開始,為後續棋子選擇合適位子
{
if(check(k)==0) //第k行的a[k]列不能放置皇後
{
a[k]++; //繼續探測當前行的下一列:a[k]+1
}
else
{
k++; //第K行的位置已經確定了,繼續尋找第k+1行皇後的位置
a[k]=1; //從第一列開始查找
}
}
else
{
if(k>num) //若滿足輸出數組的要求則輸出該數組
{
count++;
printf("[%d]: ",count);
show(num); //調用輸出函數show()
}
//如果k>num會執行下面兩行代碼,因為雖然找到了N皇後問題的一個解,但是要找的是所有解,需要回溯,從當前放置皇後的下一列繼續探測
//如果a[k]>num也會執行下面兩行代碼,就是說在當前行沒有找到可以放置皇後的位置,於是回溯,從上一行皇後位置的下一列繼續探測
k--; //棋子位置不符合要求,則退回前一步
a[k]++; //繼續試探下一列位置
}
}
printf("The count is: %d \n",count);
}
int main(void)
{
int N,d;
//system("color 2a");
do
{
printf("********************N皇後問題系統*********************\n\n");
printf(" 1. 四皇後問題 \n");
printf(" 2. 八皇後問題 \n");
printf(" 3. N 皇後問題(N<20) \n");
printf(" 4. 退出 \n");
printf("******************************************************\n");
printf("\n 從數字1-4之間的數選擇需要的操作\n\n"); /*提示輸入選項*/
printf(" 請輸入你要選擇的功能選項:__\n");
scanf("%d",&d);
switch(d)
{
case 1:
check_m(4); //4皇後問題
break;
case 2:
check_m(8); //8皇後問題
break;
case 3:
printf("請輸入N的值:_");
fflush(stdin); //清除緩沖
scanf("%d",&N);
printf("\n");
if(N>0&&N<20)
{
check_m(N); //N皇後問題
break;
}
else
{
printf("輸入錯誤,請從新輸入:");
printf("\n\n");
break;
}
case 4:
exit(0); //程序結束
}
}while(1);
system("pause");
return 0;
}
遞歸解法:
代碼如下:
#include <stdio.h>
#include <stdlib.h>
const int N=20; //最多放皇後的個數
int q[N]; //各皇後所在的行號
int cont = 0; //統計解得個數
//輸出一個解
void print(int n)
{
int i,j;
cont++;
printf("第%d個解:",cont);
for(i=1;i<=n;i++)
printf("(%d,%d) ",i,q[i]);
printf("\n");
for(i=1;i<=n;i++) //行
{
for(j=1;j<=n;j++) //列
{
if(q[i]!=j)
printf("x ");
else
printf("Q ");
}
printf("\n");
}
}
//檢驗第i行的k列上是否可以擺放皇後
int find(int i,int k)
{
int j=1;
while(j<i) //j=1~i-1是已經放置了皇後的行
{
//第j行的皇後是否在k列或(j,q[j])與(i,k)是否在斜線上
if(q[j]==k || abs(j-i)==abs(q[j]-k))
return 0;
j++;
}
return 1;
}
//放置皇後到棋盤上
void place(int k,int n)
{
int j;
if(k>n)
print(n);
else
{
for(j=1;j<=n;j++) //試探第k行的每一個列
{
if(find(k,j))
{
q[k] = j;
place(k+1,n); //遞歸總是在成功完成了上次的任務的時候才做下一個任務
}
}
}
}
int main(void)
{
int n;
printf("請輸入皇後的個數(n<=20),n=:");
scanf("%d",&n);
if(n>20)
printf("n值太大,不能求解!\n");
else
{
printf("%d皇後問題求解如下(每列的皇後所在的行數):\n",n);
place(1,n); //問題從最初狀態解起
printf("\n");
}
system("pause");
return 0;
}
二、使用位運算來求解N皇後的高效算法
核心代碼如下:
代碼如下:
void test(int row, int ld, int rd)
{
int pos, p;
if ( row != upperlim )
{
pos = upperlim & (~(row | ld | rd ));
while ( pos )
{
p = pos & (~pos + 1);
pos = pos - p;
test(row | p, (ld | p) << 1, (rd | p) >> 1);
}
}
else
++Ans;
}
初始化: upperlim = (1 << n)-1; Ans = 0;
調用參數:test(0, 0, 0);
和普通算法一樣,這是一個遞歸函數,程序一行一行地尋找可以放皇後的地方。函數帶三個參數row、ld和rd,分別表示在縱列和兩個對角線方向的限制條件下這一行的哪些地方不能放。位於該行上的沖突位置就用row、ld和rd中的1來表示。把它們三個並起來,得到該行所有的禁位,取反後就得到所有可以放的位置(用pos來表示)。
p = pos & (~pos + 1)其結果是取出最右邊的那個1。這樣,p就表示該行的某個可以放子的位置,把它從pos中移除並遞歸調用test過程。
注意遞歸調用時三個參數的變化,每個參數都加上了一個禁位,但兩個對角線方向的禁位對下一行的影響需要平移一位。最後,如果遞歸到某個時候發現row=upperlim了,說明n個皇後全放進去了,找到的解的個數加一。
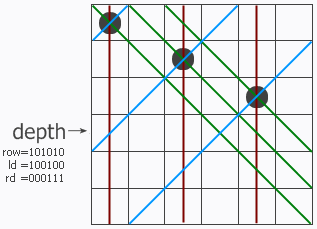
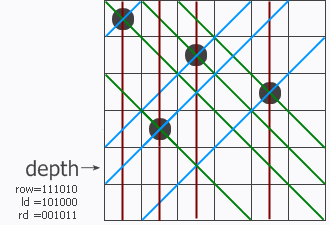
注:
upperlime:=(1 << n)-1 就生成了n個1組成的二進制數。
這個程序是從上向下搜索的。
pos & -pos 的意思就是取最右邊的 1 再組成二進制數,相當於 pos &(~pos +1),因為取反以後剛好所有數都是相反的(怎麼聽著像廢話),再加 1 ,就是改變最低位,如果低位的幾個數都是1,加的這個 1 就會進上去,一直進到 0 ,在做與運算就和原數對應的 1 重合了。舉例可以說明:
原數 0 0 0 0 1 0 0 0 原數 0 1 0 1 0 0 1 1
取反 1 1 1 1 0 1 1 1 取反 1 0 1 0 1 1 0 0
加1 1 1 1 1 1 0 0 0 加1 1 0 1 0 1 1 0 1
與運算 0 0 0 0 1 0 0 0 and 0 0 0 0 0 0 0 1
其中呢,這個取反再加 1 就是補碼,and 運算 與負數,就是按位和補碼與運算。
(ld | p)<< 1 是因為由ld造成的占位在下一行要右移一下;
(rd | p)>> 1 是因為由rd造成的占位在下一行要左移一下。
ld rd row 還要和upperlime 與運算 一下,這樣做的結果就是從最低位數起取n個數為有效位置,原因是在上一次的運算中ld發生了右移,如果不and的話,就會誤把n以外的位置當做有效位。
pos 已經完成任務了還要減去p 是因為?
while 循環是因為?
在進行到某一層的搜索時,pos中存儲了所有的可放位置,為了求出所有解,必須遍歷所有可放的位置,而每走過一個點必須要刪掉它,否則就成死循環啦!
這個是目前公認N皇後的最高效算法。
完整的代碼如下:
代碼如下:
/*
** 目前最快的N皇後遞歸解決方法
** N Queens Problem
** 試探-回溯算法,遞歸實現
*/
#include "iostream"
using namespace std;
#include "time.h"
// sum用來記錄皇後放置成功的不同布局數;upperlim用來標記所有列都已經放置好了皇後。
long sum = 0, upperlim = 1;
// 試探算法從最右邊的列開始。
void test(long row, long ld, long rd)
{
if (row != upperlim)
{
// row,ld,rd進行“或”運算,求得所有可以放置皇後的列,對應位為0,
// 然後再取反後“與”上全1的數,來求得當前所有可以放置皇後的位置,對應列改為1
// 也就是求取當前哪些列可以放置皇後
long pos = upperlim & ~(row | ld | rd);
while (pos) // 0 -- 皇後沒有地方可放,回溯
{
// 拷貝pos最右邊為1的bit,其余bit置0
// 也就是取得可以放皇後的最右邊的列
long p = pos & -pos;
// 將pos最右邊為1的bit清零
// 也就是為獲取下一次的最右可用列使用做准備,
// 程序將來會回溯到這個位置繼續試探
pos -= p;
// row + p,將當前列置1,表示記錄這次皇後放置的列。
// (ld + p) << 1,標記當前皇後左邊相鄰的列不允許下一個皇後放置。
// (ld + p) >> 1,標記當前皇後右邊相鄰的列不允許下一個皇後放置。
// 此處的移位操作實際上是記錄對角線上的限制,只是因為問題都化歸
// 到一行網格上來解決,所以表示為列的限制就可以了。顯然,隨著移位
// 在每次選擇列之前進行,原來N×N網格中某個已放置的皇後針對其對角線
// 上產生的限制都被記錄下來了
test(row + p, (ld + p) << 1, (rd + p) >> 1);
}
}
else
{
// row的所有位都為1,即找到了一個成功的布局,回溯
sum++;
}
}
int main(int argc, char *argv[])
{
time_t tm;
int n = 16;
if (argc != 1)
n = atoi(argv[1]);
tm = time(0);
// 因為整型數的限制,最大只能32位,
// 如果想處理N大於32的皇後問題,需要
// 用bitset數據結構進行存儲
if ((n < 1) || (n > 32))
{
printf(" 只能計算1-32之間\n");
exit(-1);
}
printf("%d 皇後\n", n);
// N個皇後只需N位存儲,N列中某列有皇後則對應bit置1。
upperlim = (upperlim << n) - 1;
test(0, 0, 0);
printf("共有%ld種排列, 計算時間%d秒 \n", sum, (int) (time(0) - tm));
system("pause");
return 0;
}
上述代碼還是比較容易看懂的,但我覺得核心的是在針對試探-回溯算法所用的數據結構的設計上。
程序采用了遞歸,也就是借用了編譯系統提供的自動回溯功能。
算法的核心:使用bit數組來代替以前由int或者bool數組來存儲當前格子被占用或者說可用信息,從這可以看出N個皇後對應需要N位表示。
巧妙之處在於:以前我們需要在一個N*N正方形的網格中挪動皇後來進行試探回溯,每走一步都要觀察和記錄一個格子前後左右對角線上格子的信息;采用bit位進行信息存儲的話,就可以只在一行格子也就是(1行×N列)個格子中進行試探回溯即可,對角線上的限制被化歸為列上的限制。
程序中主要需要下面三個bit數組,每位對應網格的一列,在C中就是取一個整形數的某部分連續位即可。 row用來記錄當前哪些列上的位置不可用,也就是哪些列被皇後占用,對應為1。ld,rd同樣也是記錄當前哪些列位置不可用,但是不表示被皇後占用,而是表示會被已有皇後在對角線上吃掉的位置。這三個位數組進行“或”操作後就是表示當前還有哪些位置可以放置新的皇後,對應0的位置可放新的皇後。如下圖所示的8皇後問題求解得第一步:
row: [ ][ ][ ][ ][ ][ ][ ][*]
ld: [ ][ ][ ][ ][ ][ ][*][ ]
rd: [ ][ ][ ][ ][ ][ ][ ][ ]
--------------------------------------
row|ld|rd: [ ][ ][ ][ ][ ][ ][*][*]
所有下一個位置的試探過程都是通過位操作來實現的,這是借用了C語言的好處,詳見代碼注釋。
關於此算法,如果考慮N×N棋盤的對稱性,對於大N來說仍能較大地提升效率!
位操作--對優化算法有了個新的認識
這個是在csdn找到的一個N皇後問題最快的算法,看了好一會才明白,這算法巧妙之處我認為有2個:
1、以前都是用數組來描述狀態,而這算法采用是的位來描述,運算速度可以大大提升,以後寫程序對於描述狀態的變量大家可以借鑒這個例子,會讓你的程序跑得更快
2、描述每行可放置的位置都是只用row,ld,rd這3個變量來描述,這樣使得程序看起來挺簡潔的。

