假設有一個string “BaSiC”,需要將它轉變為大小寫,那麼該如何轉換?
最簡單的方式:調用api:
string str = "BaSiC";
string strUpper = str.ToUpper();
string strLower = str.ToLower();
第二種方法:調用Char.ToUpper(),Char.ToLower()方法,同樣是調用api
第三種方法:使用for循環來判斷,如果是大寫就,如果是小寫就..
首先觀察大寫字母和小寫字母的異同:
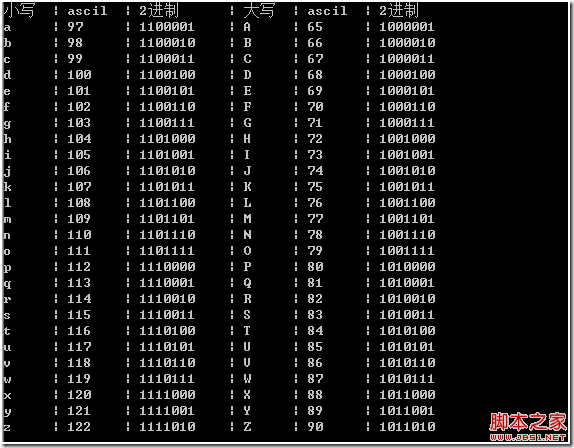
打印上面的代碼如下,有興趣的可以自己試試打印這樣的表格出來:
Console.WriteLine("{0,-3} | {1,-6} | {2,-8} | {3,-3} | {4,-6} | {5,-8}",
"小寫", "ascil", "2進制", "大寫", "ascil", "2進制");
IEnumerable<char> chars = Enumerable.Range('a', 'z' - 'a' + 1).Select(i => (char)i);
foreach (char c in chars)
{
char upperC = char.ToUpper(c);
Console.WriteLine("{0,-5} | {1,-6} | {2,-10} | {3,-5} | {4,-6} | {5,-10}",
c, (int)c, Convert.ToString(c, 2),
upperC, (int)upperC, Convert.ToString(upperC, 2));
}
從上面很容易看的出來'a' 比大寫的'A' 的ascil多32,從這點出發就可以得到下面的代碼:
private static char[] GetUpperChars(string str)
{
char[] chars = str.ToCharArray();
for (int i = 0; i < chars.Length; i++)
{
if (char.IsLower(chars[i]))
{
chars[i] = (char)(chars[i] - 32);
}
}
return chars;
}
這段代碼使用for循環並加入判斷,如果是小寫,則將其值減去32,調用也比較簡單:
string strUpper2 = new string(GetUpperChars(str));
這段代碼唯一的缺點是進行了IsLower的判斷,可不可以在沒有判斷的情況下來修改chars使其變成大寫呢?
如果從Ascii 的角度來解決這個問題,那麼我們就必須使用大小寫的判斷,我在匯編語言的書上看到了這句話:
如果一個問題的解決方案,使我們陷入一種矛盾之中,那麼很可能是我們考慮問題的出發點有了問題,或者說我們起初運用的規律並不適合。
這段話的意思是,可能我們應該從其他角度來觀察,而不應該從Ascii的角度來觀察。
如果不從Ascii的角度來觀察,那還能從哪裡來觀察呢?
可以從2進制的角度來觀察。
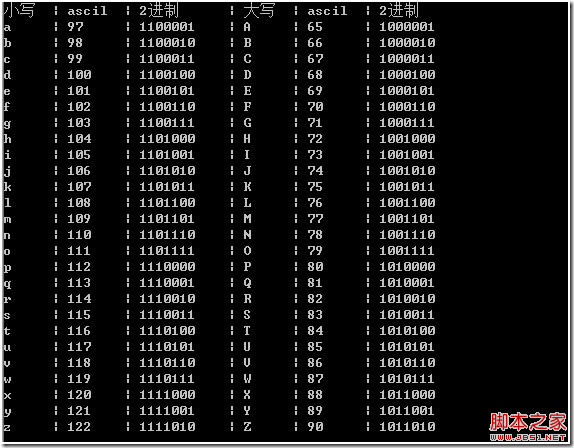
還是這幅圖,只是我們的觀察角度變成了2進制。
a 的2進制:1100001, b的2進制1100010,..
A 的2進制: 1000001, B的2進制1000010,..
可以知道a的第5位是1,而A的第5位是0,(從右邊往左邊數,0開始,後面得第幾位都這樣數)
b的第5位是1,而B的第5位是0,
..
所以如果要將一個字符串變成大寫,只需要將字符串的所有字符的第5位全部變成1就可以了。
而如何將一個字符的第5位變成1呢?
答案是使用And(位運算)操作.
首先a 是個7位字符,只所以是7位,是因為在制定Ascii的時候位比較貴,8位比較浪費,而6位又不夠,所以ascii碼是7位的,這點從
a 是1100001 就可以看出了,總共7位。
它可以和0101-1111 或者是1101-1111,進行And
在C#中And 是&
所以你可能會將函數修改為:
for (int i = 0; i < chars.Length; i++)
{
chars[i] = (char)(chars[i] & 11011111);
}
先停一下,你認為上面的寫法正確嗎?
然後運行,結果卻發現:

為什麼?
這是因為C#中的& 默認操作的是十進制的數字,所以11011111,
就會變成一千一百零一萬一千一百一十一
所以要將2進制的11011111 變成10進制,如何轉變?
int value = Convert.ToInt32("11011111", 2);
value的值是223.所以代碼修改為:
for (int i = 0; i < chars.Length; i++)
{
chars[i] = (char)(chars[i] & 223);
}
運行可以得到正確的結果:
或者使用16進制來表示:1101-1111 ,的16進制是:
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
0 1 2 3 4 5 6 7 8 9 A B C D E F
1101=2^3+2^2+1=8+4+1=13 = D
1111=2^3+2^2+2^1+2^0=8+4+2+1=15 = F
所以可以將上面的代碼修改為:
chars[i] = (char)(chars[i] & 0xdf);
同樣因為只是第5位不同,而第7位會被忽略。所以和 0101-1111進行and操作也可以得到正確的答案:
而0101-1111 的16進制是0x5f.所以代碼可以變成:
chars[i] = (char)(chars[i] & 0x5f);