全排列輸出:
解法一:
代碼如下:
<SPAN >#include <stdio.h>
/*
遞歸思想:
取出數組第一個元素放到最後一個元素 即a[0] 和a[n]交換 然後一次遞歸a[n] 個元素的全排列
1 如果數組只有一個元素 n=1 a={1} 則全排列就是{1}
2 如果有兩個元素 n=2 a={1,2} 則全排列是
{2,1} a[1]與a[2]交換 交換後求a[2-1]={2}的全排列 歸結到 1
{1,2} a[2]與a[2]交換 交換後求a[2-1]={1}的全排列 歸結到 1
3 如果有三個元素 n=3 a={1,2,3} 則全排列是
{{2,3},1} a[1]和a[3]交換 交換後求a[3-1]={2,3} 的全排列 歸結到 2
{{1,3},2} a[2] a[3] 交換 交換後求 a[3-1]={1,3} 的全排列 歸結到 2
{1,2},3} a[3] a[3] 交換 交換後求 a[3-1]={1,2} 的全排列 歸結到 2
*/
void swap(int a[],int size)
{
int i,t;
if(size==0)
{
for(i=0;i<5;i++)
{
printf("%c ",a[i]);
}
printf("\n");
return;
}
else
{
for(i=0;i<=size;i++) //元素 進行全部循環
{
//寫在swap()之前,進行遞歸傳值 出口點要傳入函數
t=a[i];a[i]=a[size];a[size]=t;
swap(a,size-1);
//數組元素還原 開始是什麼 現在還是什麼 位置改變後 變成原來位置
// 便於從a[1] 到a[n] 和最後一個元素交換位置
t=a[i];a[i]=a[size];a[size]=t;
}
}
}
int main()
{
int a[5],i;
for(i=0;i<5;i++)
{
a[i]=97+i;
}
swap(a,4);
//printf("\n%d",m);
return 0;
}</SPAN>
解法二:
代碼如下:
<SPAN >#include <stdio.h>
//思路 分別求出以1 2 3 4 5 開頭 剩下數字的全排列 一直到簡化為一個數字
void swap(int a[],int k)
{
int i,m,t=0;
if(k==5)
{
for(i=0;i<5;i++)
{
printf("%d ",a[i]);
}
//k++;
printf("\n");
}
for(i=k;i<5;i++)
{
{m=a[k];a[k]=a[i];a[i]=m;}
swap(a,k+1);
{m=a[k];a[k]=a[i];a[i]=m;}
}
}
int main()
{
int a[5]={1,2,3,4,5}; //進行遞歸運算的數值
swap(a,0); //函數調用
return 0;
}
</SPAN>
m個數中取n個進行排列:
代碼如下:
#include <stdio.h>
void swap(int a[],int b[],int i,int size)
{
int k,j,temp;
if(i==3)
{
for(k=0;k<3;k++)
{
printf("%d ",b[k]);
}
printf("\n");
return;
}
else
{
for(j=0;j<size;j++)
{
b[i]=a[j];
temp=a[j];a[j]=a[size-1];a[size-1]=temp;
swap(a,b,i+1,size-1);
temp=a[j];a[j]=a[size-1];a[size-1]=temp;
}
}
}
int main()
{
int a[5]={1,2,3,4,5},b[3];//求5個數中三個數的全排列
swap(a,b,0,5);
return 0;
}
m個數取n個進行組合:
[10反轉置換法]
算法思想:
(1) 初始化一個m個元素的數組(全部由0,1組成),將前n個初始化為1,後面的為0。這時候就可以輸出第一個組合序列了。
(2) 從前往後找,找到第一個10組合,將其反轉成01,然後將這個10組合前面的所有1,全部往左邊推 ,即保證其前面的1都在最左邊。這時又可以輸出一組組合序列了。
(3) 重復第(2)步,知道找不到10組合位置。這時已經輸出了全部的可能
代碼如下:
#include <stdio.h>
#include <stdlib.h>
void putout(int * num,int m)
{
int i;
for(i=0;i<m;i++)
{
if(*(num+i))
printf("%d ",i+1);
}
printf("\n");
}
int check(int *num,int m,int n)
{
int flag=1,i;//當flag=1時,繼續while循環 反之,退出循環
for(i=0;i<m-n;i++)
{
if(*(num+i))
{
return 1;
}
}
return 0;
}
void choseNum(int *num,int m,int n)
{
int i,j;
putout(num,m); //輸出第一個組合
while(1)
{
int count=0; //注意count位置 就他調試了半天
//找第一個1 0組合
for(i=0;i<m-1;i++)
{
if(*(num+i)==1&&*(num+i+1)==0)
{
*(num+i)=0;
*(num+i+1)=1;
break;
}
if(*(num+i)) //統計前面出現出現1的次數
count++;
}
for(j=0;j<i;j++)
{
if(j<count) //將前面幾個數全為1
{
*(num+j)=1;
}
else //後幾個數為0
{
*(num+j)=0;
}
}
putout(num,m);
if(check(num,m,n)!=1)
break;
}
free(num);
}
int main()
{
int m,n;//從m個數中找n個求組合
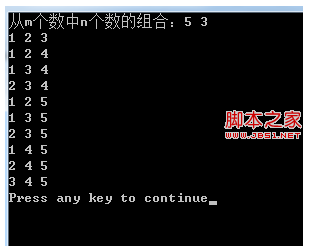
printf("從m個數中n個數的組合:");
scanf("%d %d",&m,&n);
int *num,i;
//int count;
num=(int *)malloc(sizeof(int)*m);
for(i=0;i<m;i++)
{
if(i<n)
*(num+i)=1;
else
*(num+i)=0;
}
choseNum(num,m,n);
return 0;
}
結果實例: