c語言算術運算符越界問題解決方案

大量的安全漏洞是由於計算機算術運算的微妙細節引起的, 具體的C語言, 諸如符號數和無符號數之間轉換, 算術運算的越界都會導致不可預知的錯誤和安全漏洞, 具體的案例數不勝數.

作為一個系統程序員, 有必要對這些細節有深入的了解. 本篇參考csapp, 主要介紹如何判斷算術運算的越界問題.

(雖然本篇的代碼經過大量的測試, 但本人仍然無法保證代碼的正確性, 希望大家糾錯).
講解的原則是"擺定理, 不證明, 寫代碼". 具體的證明過程在csapp中有詳細的講解, 也不是太難. 主要使用關鍵定理來寫代碼. Go~
問題一: 無符號數的加法越界問題
[定理]

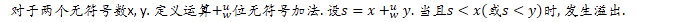
[理解]
這個定理比較容易, 也比較能讓人接受. 不解釋啦.
代碼如下：

/* Determine whether arguments can be added without overflow */
int uadd_ok(unsigned int x, unsigned int y)
{
return !(x+y < x);
}

問題二: 無符號數的減法越界問題
[定理]

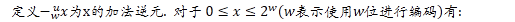
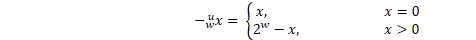
[理解]
1. 計算機中沒有減法, x-y = x+(-y), 這裡的-y就是上述的y的加法逆元. 不管是有符號還是無符號, 都是轉換為加法運算. 只是加法逆元的定義不同.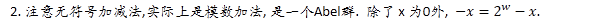

3. C語言保證 -x = ~x+1; 可以驗證這種方式與上面公式等價.
4. s=x-y = x+(-y). 那麼 不會溢出 等價於 y不為0 或者 !uadd_ok(x, -y).

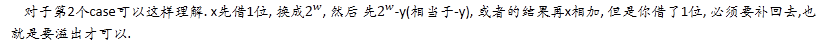
代碼如下：

/* Determine whether argumnts can be substracted without overflow */
int usub_ok(unsigned int x, unsigned int y)
{
return !y || !uadd_ok(x, -y);
}

問題三: 無符號數的乘法越界問題
[定理]

[理解]
等價條件可以相互推導即可.
代碼如下：

/* Determine whether arguments can be multiplied without overflow */
int umul_ok(unsigned int x, unsigned int y)
{
unsigned int p = x * y;
return !x || p/x==y;
}

問題四: 有符號數的加法越界問題
[定理]
對於兩個有符號數x, y. 越界的等價條件是x,y為負數, x+y為正數或者x,y為正數, x+y為負數.
[理解]
這個定理比較容易.
代碼如下：

/* Determine whether arguments can be added without overflow */
int tadd_ok(int x, int y)
{
return !(x<0&&y<0&&x+y>0 || x>0&&y>0&&x+y<0);
}

問題五: 有符號數的減法越界問題
[定理]

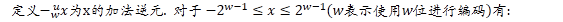
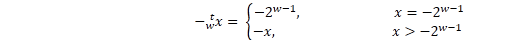
[理解]
同無符號的減法一樣, 只是加法逆元的定義不同, 但是位模式是一樣的. C語言可以保證-x=~x+1. 同樣也分兩種情況討論.見代碼.

代碼如下：

/* Determine whether arguments can be subtracted without overflow */
int tsub_ok(int x, int y)
{
　　#if 0
　　if (y == INT_MIN)
　　return x<0;
　　else
　　return tadd_ok(x, -y);
　　#endif
　　return y==INT_MIN&&x<0 || y!=INT_MIN&&tadd_ok(x, -y);
}

問題六: 有符號數的乘法越界問題
[定理]
完全同無符號的乘法一樣.
代碼如下：

/* Determine whether arguments can be multiplied without overflow. */
int tmul_ok(int x, int y)
{
#if 0
int p = x * y;
return !x || p/x==y;
#endif
return umul_ok(x, y); /* 直接調用 */
}