轉載請注明出處：http://blog.csdn.net/ns_code/article/details/19174553

Huffman Tree簡介

赫夫曼樹（Huffman Tree），又稱最優二叉樹，是一類帶權路徑長度最短的樹。假設有n個權值{w1,w2,...,wn}，如果構造一棵有n個葉子節點的二叉樹，而這n個葉子節點的權值是{w1,w2,...,wn}，則所構造出的帶權路徑長度最小的二叉樹就被稱為赫夫曼樹。

這裡補充下樹的帶權路徑長度的概念。樹的帶權路徑長度指樹中所有葉子節點到根節點的路徑長度與該葉子節點權值的乘積之和，如果在一棵二叉樹中共有n個葉子節點，用Wi表示第i個葉子節點的權值，Li表示第i個也葉子節點到根節點的路徑長度，則該二叉樹的帶權路徑長度 WPL=W1*L1 + W2*L2 + ... Wn*Ln。

根據節點的個數以及權值的不同，赫夫曼樹的形狀也各不相同，赫夫曼樹具有如下特性：

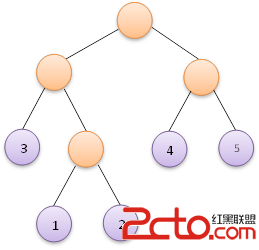
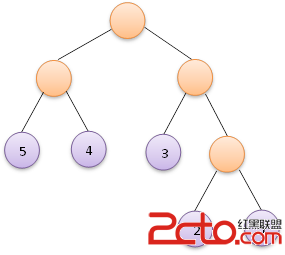
對於同一組權值，所能得到的赫夫曼樹不一定是唯一的。赫夫曼樹的左右子樹可以互換，因為這並不影響樹的帶權路徑長度。帶權值的節點都是葉子節點，不帶權值的節點都是某棵子二叉樹的根節點。權值越大的節點越靠近赫夫曼樹的根節點，權值越小的節點越遠離赫夫曼樹的根節點。赫夫曼樹中只有葉子節點和度為2的節點，沒有度為1的節點。一棵有n個葉子節點的赫夫曼樹共有2n-1個節點。

Huffman Tree的構建

赫夫曼樹的構建步驟如下： 1、將給定的n個權值看做n棵只有根節點（無左右孩子）的二叉樹，組成一個集合HT，每棵樹的權值為該節點的權值。 2、從集合HT中選出2棵權值最小的二叉樹，組成一棵新的二叉樹，其權值為這2棵二叉樹的權值之和。 3、將步驟2中選出的2棵二叉樹從集合HT中刪去，同時將步驟2中新得到的二叉樹加入到集合HT中。 4、重復步驟2和步驟3，直到集合HT中只含一棵樹，這棵樹便是赫夫曼樹。
假如給定如下5個權值：

則按照以上步驟，可以構造出如下面左圖所示的赫夫曼樹，當然也可能構造出如下面右圖所示的赫夫曼樹，這並不是唯一的。

Huffman編碼

赫夫曼樹的應用十分廣泛，比如眾所周知的在通信電文中的應用。在等傳送電文時，我們希望電文的總長盡可能短，因此可以對每個字符設計長度不等的編碼，讓電文中出現較多的字符采用盡可能短的編碼。為了保證在譯碼時不出現歧義，我們可以采取如下圖所示的編碼方式：


即左分支編碼為字符0，右分支編碼為字符1，將從根節點到葉子節點的路徑上分支字符組成的字符串作為葉子節點字符的編碼，這便是赫夫曼編碼。我們根據上面左圖可以得到各葉子節點的赫夫曼編碼如下：
權值為5的也自己節點的赫夫曼編碼為：11 權值為4的也自己節點的赫夫曼編碼為：10 權值為3的也自己節點的赫夫曼編碼為：00 權值為2的也自己節點的赫夫曼編碼為：011 權值為1的也自己節點的赫夫曼編碼為：010
而對於上面右圖，則可以得到各葉子節點的赫夫曼編碼如下： 權值為5的也自己節點的赫夫曼編碼為：00 權值為4的也自己節點的赫夫曼編碼為：01 權值為3的也自己節點的赫夫曼編碼為：10 權值為2的也自己節點的赫夫曼編碼為：110 權值為1的也自己節點的赫夫曼編碼為：111

Huffman編碼的C實現

由於赫夫曼樹中沒有度為1的節點，則一棵具有n個葉子節點的的赫夫曼樹共有2n-1個節點（最後一條特性），因此可以將這些節點存儲在大小為2n-1的一維數組中。我們可以用以下數據結構來表示赫夫曼樹和赫夫曼編碼：

/*
赫夫曼樹的存儲結構，它也是一種二叉樹結構，
這種存儲結構既適合表示樹，也適合表示森林。
*/
typedef struct Node
{
	int weight;                //權值
	int parent;                //父節點的序號，為0的是根節點
	int lchild,rchild;         //左右孩子節點的序號，為0的是葉子節點
}HTNode,*HuffmanTree;          //用來存儲赫夫曼樹中的所有節點
typedef char **HuffmanCode;    //用來存儲每個葉子節點的赫夫曼編碼

根據赫夫曼樹的構建步驟，我們可以寫出構建赫夫曼樹的代碼如下：

/*
根據給定的n個權值構造一棵赫夫曼樹,wet中存放n個權值
*/
HuffmanTree create_HuffmanTree(int *wet,int n)
{
	//一棵有n個葉子節點的赫夫曼樹共有2n-1個節點
	int total = 2*n-1;
	HuffmanTree HT = (HuffmanTree)malloc(total*sizeof(HTNode));
	if(!HT)
	{
		printf("HuffmanTree malloc faild!");
		exit(-1);
	}
	int i;

	//HT[0],HT[1]...HT[n-1]中存放需要編碼的n個葉子節點
	for(i=0;i    上述代碼中調用到了select_minium（）函數，它表示從集合中選出兩個最小的二叉樹，代碼如下：
/*
從HT數組的前k個元素中選出weight最小且parent為0的兩個，分別將其序號保存在min1和min2中
*/
void select_minium(HuffmanTree HT,int k,int &min1,int &min2)
{
	min1 = min(HT,k);
	min2 = min(HT,k);
}
    這裡調用到的min（）函數代碼如下：
/*
從HT數組的前k個元素中選出weight最小且parent為0的元素，並將該元素的序號返回
*/
int min(HuffmanTree HT,int k)
{
	int i = 0;
	int min;        //用來存放weight最小且parent為0的元素的序號
	int min_weight; //用來存放weight最小且parent為0的元素的weight值

	//先將第一個parent為0的元素的weight值賦給min_weight,留作以後比較用。
	//注意，這裡不能按照一般的做法，先直接將HT[0].weight賦給min_weight，
	//因為如果HT[0].weight的值比較小，那麼在第一次構造二叉樹時就會被選走，
	//而後續的每一輪選擇最小權值構造二叉樹的比較還是先用HT[0].weight的值來進行判斷，
	//這樣又會再次將其選走，從而產生邏輯上的錯誤。
	while(HT[i].parent != 0)
		i++;
	min_weight = HT[i].weight;
	min = i;

	//選出weight最小且parent為0的元素，並將其序號賦給min
	for(;i    構建了赫夫曼樹，便可以進行赫夫曼編碼了，要求赫夫曼編碼，就需要遍歷出從根節點到葉子節點的路徑，我們這裡采用從葉子節點到根節點逆向遍歷求每個字符的赫夫曼編碼，代碼如下：
/*
從葉子節點到根節點逆向求赫夫曼樹HT中n個葉子節點的赫夫曼編碼，並保存在HC中
*/
void HuffmanCoding(HuffmanTree HT,HuffmanCode &HC,int n)
{
	//用來保存指向每個赫夫曼編碼串的指針
	HC = (HuffmanCode)malloc(n*sizeof(char *));
	if(!HC)
	{
		printf("HuffmanCode malloc faild!");
		exit(-1);
	}

	//臨時空間，用來保存每次求得的赫夫曼編碼串
	char *code = (char *)malloc(n*sizeof(char));
	if(!code)
	{
		printf("code malloc faild!");
		exit(-1);
	}

	code[n-1] = '\0';  //編碼結束符，亦是字符數組的結束標志
	//求每個字符的赫夫曼編碼
	int i;
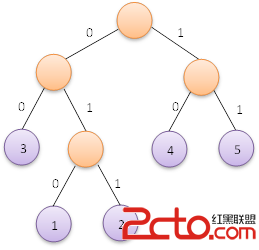
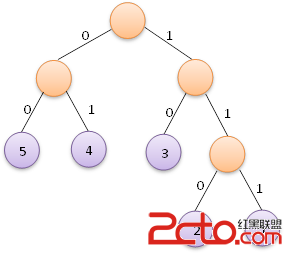
	for(i=0;i    我們以上面給出的5、4、3、2、1這五個權值為例，得到的編碼結果如下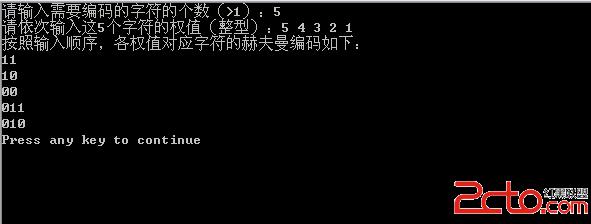：    這恰好符合上面兩棵赫夫曼樹中左邊的那一棵樹的赫夫曼編碼，因此改程序構造出的赫夫曼樹即為上圖左邊的那棵。
    完整的代碼下載地址：http://download.csdn.net/detail/mmc_maodun/6923741