在之前的博文《算法導論 之 平衡二叉樹 - 構造、插入、查詢、銷毀》和《算法導論 之 平衡二叉樹 - 打印》中已經給出了構建、插入、查詢、打印和銷毀平衡二叉樹的C語言實現過程,此篇中出現的相關結構體、宏、枚舉、函數可以到以上兩篇中查找。之所以現在才來寫平衡二叉樹的刪除操作,主要是其過程相對比較復雜,且測試和實現過程中總是出現各種各樣的問題,直到今天才徹底解決,平衡二叉樹的處理終於可以告一段落。
① 被刪的節點是葉子節點
處理思路:將該節點直接從樹中刪除,並利用遞歸的特點和高度的變化,反向推算其父節點和祖先節點是否失衡。如果失衡,則判斷是那種類型的失衡(LL、LR、RR、RL),再對失衡節點進行旋轉處理,直到根節點或高度不再變化。
② 被刪的節點只有左子樹或只有右子樹
處理思路:將左子樹(右子樹)替代原有節點的位置,並利用遞歸的特點和高度的變化,反向推算父節點和祖先節點是否失衡。如果失衡,則判斷是那種類型的失衡(LL、LR、RR、RL),再對失衡節點進行旋轉處理,直到根節點或高度不再發生變化。
③ 被刪的節點既有左子樹又有右子樹
處理思路:找到被刪節點的左子樹的最右端的節點rnode,將rnode的值賦給node,再把rnode的左孩子替換rnode的位置,在把rnode釋放掉,並利用遞歸特點,反向推斷rnode的父節點和祖父節點是否失衡。如果失衡,則判斷是哪種類型的失衡(LL、LR、RR、RL),再對失衡的節點進行旋轉處理,直到根節點或高度不再發生變化。
/******************************************************************************
**函數名稱: avl_delete
**功 能: 刪除key值節點(對外接口)
**輸入參數:
** tree: 平衡二叉樹
** key: 被刪除的關鍵字
**輸出參數: NONE
**返 回: AVL_SUCCESS:成功 AVL_FAILED:失敗
**實現描述:
**注意事項:
**作 者: # Qifeng.zou # 2013.12.19 #
******************************************************************************/
int avl_delete(avl_tree_t *tree, int key)
{
bool lower = false; /* 記錄高度是否降低 */
if(NULL == tree->root)
{
return AVL_SUCCESS;
}
return avl_search_and_delete(tree, tree->root, key, &lower);
}
代碼1 刪除節點(外部接口)
/******************************************************************************
**函數名稱: avl_search_and_delete
**功 能: 搜索並刪除指定的key值節點(內部接口)
**輸入參數:
** tree: 平衡二叉樹
** node: 以node為根節點的子樹
** key: 被刪除的關鍵字
**輸出參數:
** lower: 高度是否降低
**返 回: AVL_SUCCESS:成功 AVL_FAILED:失敗
**實現描述:
**注意事項:
**作 者: # Qifeng.zou # 2013.12.19 #
******************************************************************************/
int avl_search_and_delete(avl_tree_t *tree, avl_node_t *node, int key, bool *lower)
{
avl_node_t *parent = node->parent;
/* 1. 查找需要被刪除的節點 */
if(key < node->key) /* 左子樹上查找 */
{
if(NULL == node->lchild)
{
return AVL_SUCCESS;
}
avl_search_and_delete(tree, node->lchild, key, lower);
if(true == *lower)
{
return avl_delete_left_balance(tree, node, lower);
}
return AVL_SUCCESS;
}
else if(key > node->key) /* 右子樹上查找 */
{
if(NULL == node->rchild)
{
return AVL_SUCCESS;
}
avl_search_and_delete(tree, node->rchild, key, lower);
if(true == *lower)
{
return avl_delete_right_balance(tree, node, lower);
}
return AVL_SUCCESS;
}
/* 2. 已找到將被刪除的節點node */
/* 2.1 右子樹為空, 只需接它的左子樹(葉子節點也走這) */
if(NULL == node->rchild)
{
*lower = true;
avl_replace_child(tree, parent, node, node->lchild);
free(node), node = NULL;
return AVL_SUCCESS;
}
/* 2.2 左子樹空, 只需接它的右子樹 */
else if(NULL == node->lchild)
{
*lower = true;
avl_replace_child(tree, parent, node, node->rchild)
free(node), node=NULL;
return AVL_SUCCESS;
}
/* 2.3 左右子樹均不為空: 查找左子樹最右邊的節點 替換被刪的節點 */
avl_replace_and_delete(tree, node, node->lchild, lower);
if(true == *lower)
{
avl_print(tree);
return avl_delete_left_balance(tree, node, lower);
}
return AVL_SUCCESS;
}
代碼2 查找並刪除節點(內部接口)
/******************************************************************************
**函數名稱: avl_replace_and_delete
**功 能: 找到替換節點, 並替換被刪除的節點(內部接口)
**輸入參數:
** tree: 平衡二叉樹
** dnode: 將被刪除的節點
** rnode: 此節點最右端的節點將會用來替換被刪除的節點.
**輸出參數:
** lower: 高度是否變化
**返 回: AVL_SUCCESS:成功 AVL_FAILED:失敗
**實現描述:
**注意事項:
** >> 在此其實並不會刪除dnode, 而是將rnode的值給了dnode, 再刪了rnode.
** 因為在此使用的遞歸算法, 如果真把dnode給釋放了,會造成壓棧的信息出現錯誤!
**作 者: # Qifeng.zou # 2013.12.19 #
******************************************************************************/
int avl_replace_and_delete(avl_tree_t *tree, avl_node_t *dnode, avl_node_t *rnode, bool *lower)
{
avl_node_t *parent = NULL, *rparent = NULL;
if(NULL == rnode->rchild)
{
*lower = true;
parent = dnode->parent;
rparent = rnode->parent;
dnode->key = rnode->key; /* 注: 將rnode的值給了dnode */
if(rnode == dnode->lchild)
{
avl_set_lchild(dnode, rnode->lchild);
/* rnode->parent == dnode節點可能失衡,此處理交給前棧的函數處理 */
}
else
{
avl_set_rchild(rparent, rnode->lchild);
/* rnode的父節點可能失衡,此處理交給前棧的函數處理 */
}
free(rnode), rnode=NULL; /* 注意: 釋放的不是dnode, 而是rnode */
return AVL_SUCCESS;
}
avl_replace_and_delete(tree, dnode, rnode->rchild, lower);
if(true == *lower)
{
/* dnode的父節點可能失衡,此處理交給前棧的函數處理
但dnode可能使用,因此必須在此自己處理 */
avl_delete_right_balance(tree, rnode, lower);
}
return AVL_SUCCESS;
}
代碼3 替換並刪除節點(內部接口)
/******************************************************************************
**函數名稱: avl_delete_left_balance
**功 能: 節點node的左子樹某節點被刪除, 左高度降低後, 平衡化處理(內部接口)
**輸入參數:
** tree: 平衡二叉樹
** node: 節點node的左子樹的某個節點已被刪除
**輸出參數:
** lower: 高度是否變化
**返 回: AVL_SUCCESS:成功 AVL_FAILED:失敗
**實現描述:
**注意事項:
**作 者: # Qifeng.zou # 2013.12.19 #
******************************************************************************/
int avl_delete_left_balance(avl_tree_t *tree, avl_node_t *node, bool *lower)
{
avl_node_t *rchild = NULL, *rlchild = NULL, *parent = node->parent;
switch(node->bf)
{
case LH: /* 左高: 左子樹高度減1 樹變矮 */
{
node->bf = EH;
*lower = true;
break;
}
case EH: /* 等高: 左子樹高度減1 樹高度不變 */
{
node->bf = RH;
*lower = false;
break;
}
case RH: /* 右高: 左子樹高度減1 樹失去平衡 */
{
rchild = node->rchild;
switch(rchild->bf)
{
case EH: /* RR型: 向左旋轉 */
case RH: /* RR型: 向左旋轉 */
{
if(EH == rchild->bf)
{
*lower = false;
rchild->bf = LH;
node->bf = RH;
}
else if(RH == rchild->bf)
{
*lower = true;
rchild->bf = EH;
node->bf = EH;
}
avl_set_rchild(node, rchild->lchild);
avl_set_lchild(rchild, node);
avl_replace_child(tree, parent, node, rchild);
break;
}
case LH: /* RL型: 先向右旋轉 再向左旋轉 */
{
*lower = true;
rlchild = rchild->lchild;
switch(rlchild->bf)
{
case LH:
{
node->bf = EH;
rchild->bf = RH;
rlchild->bf = EH;
break;
}
case EH:
{
node->bf = EH;
rchild->bf = EH;
rlchild->bf = EH;
break;
}
case RH:
{
node->bf = LH;
rchild->bf = EH;
rlchild->bf = EH;
break;
}
}
avl_set_rchild(node, rlchild->lchild);
avl_set_lchild(rchild, rlchild->rchild);
avl_set_lchild(rlchild, node);
avl_set_rchild(rlchild, rchild);
avl_replace_child(tree, parent, node, rlchild);
break;
}
}
break;
}
}
return AVL_SUCCESS;
}
代碼4 左子樹高度降低後平衡化處理
/******************************************************************************
**函數名稱: avl_delete_right_balance
**功 能: 節點node的右子樹某節點被刪除, 左高度降低後, 平衡化處理(內部接口)
**輸入參數:
** tree: 平衡二叉樹
** node: 節點node的右子樹的某個節點已被刪除
**輸出參數:
** lower: 高度是否變化
**返 回: AVL_SUCCESS:成功 AVL_FAILED:失敗
**實現描述:
**注意事項:
**作 者: # Qifeng.zou # 2013.12.19 #
******************************************************************************/
int avl_delete_right_balance(avl_tree_t *tree, avl_node_t *node, bool *lower)
{
avl_node_t *lchild = NULL, *lrchild = NULL, *parent = node->parent;
switch(node->bf)
{
case LH: /* 左高: 右子樹高度減1 樹失去平衡 */
{
lchild = node->lchild;
switch(lchild->bf)
{
case EH: /* LL型: 向右旋轉 */
case LH: /* LL型: 向右旋轉 */
{
if(EH == lchild->bf)
{
*lower = false;
lchild->bf = RH;
node->bf = LH;
}
else
{
*lower = true;
lchild->bf = EH;
node->bf = EH;
}
avl_set_lchild(node, lchild->rchild);
avl_set_rchild(lchild, node);
avl_replace_child(tree, parent, node, lchild);
break;
}
case RH: /* LR型: 先向左旋轉 再向右旋轉 */
{
*lower = true;
lrchild = lchild->rchild;
switch(lrchild->bf)
{
case LH:
{
node->bf = RH;
lchild->bf = EH;
lrchild->bf = EH;
break;
}
case EH:
{
node->bf = EH;
lchild->bf = EH;
lrchild->bf = EH;
break;
}
case RH:
{
node->bf = EH;
lchild->bf = LH;
lrchild->bf = EH;
break;
}
}
avl_set_lchild(node, lrchild->rchild);
avl_set_rchild(lchild, lrchild->lchild);
avl_set_rchild(lrchild, node);
avl_set_lchild(lrchild, lchild);
avl_replace_child(tree, parent, node, lrchild);
break;
}
}
break;
}
case EH: /* 等高: 右子樹高度減1 樹高度不變 */
{
node->bf = LH;
*lower = false;
break;
}
case RH: /* 右高: 右子樹高度減1 樹變矮 */
{
node->bf = EH;
*lower = true;
break;
}
}
return AVL_SUCCESS;
}
代碼5 右子樹高度降低後 平衡化處理
/* # 檢測節點的指針是否存在異常 # 很有效! */
void avl_assert(avl_node_t *node)
{
if((NULL == node)
|| (NULL == node->parent))
{
return;
}
if((node->parent->lchild != node)
&& (node->parent->rchild != node))
{
assert(0);
}
if((node->parent == node->lchild)
|| (node->parent == node->rchild))
{
assert(0);
}
}
代碼6 節點檢測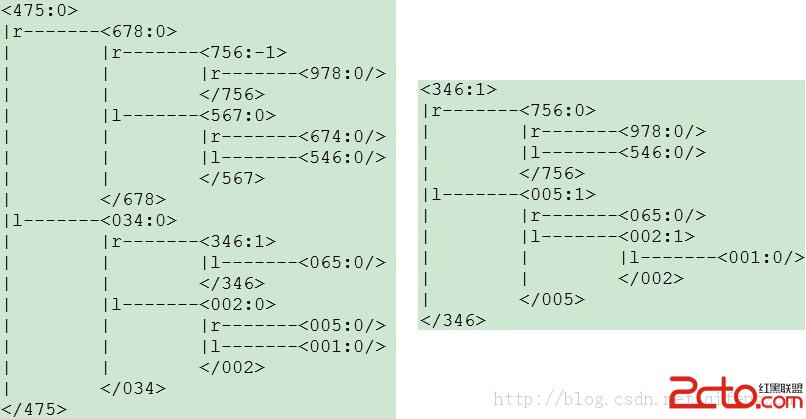
圖1 測試結果
—— 鄒祁峰
2013年12月20日 12時