之前寫拉一個random_n的算法實現,雖然簡單易懂,但是算法的效率相對來說不算很高,節省拉空間,只用到拉一個數組實現。
這個random_n的實現用到拉兩個數組,子函數中的數組在函數棧銷毀時釋放空間。最好和最壞運行時間都是O(N )。主要時利用拉空間換時間。
具體的代碼實現如下:
#include<stdio.h>
#include<stdlib.h>
#define MAX_NUM 10
void random_n(int a[],int n);
int main()
{
int a[MAX_NUM],i=0,j=0;
while(j<MAX_NUM)
{
a[j]=-1;
j++;
}
random_n(a,MAX_NUM);
while(i<MAX_NUM)
{
printf("%d\t",a[i]);
i++;
}
printf("\n");
return 0;
}
void random_n(int a[],int n)
{
int temp[n],k=0,count=0,x=0;
while(k<n)
{
temp[k]=k;
k++;
}
srand(time(0));
count=n;
k=0;
while(count)
{
x=rand()%count;
a[k]=temp[x];
printf("X= %d\t temp= %d \n",x,a[k]);
temp[x]=temp[count];
count=count-1;
k=k+1;
x=0;
}
}
調試和運行結果:
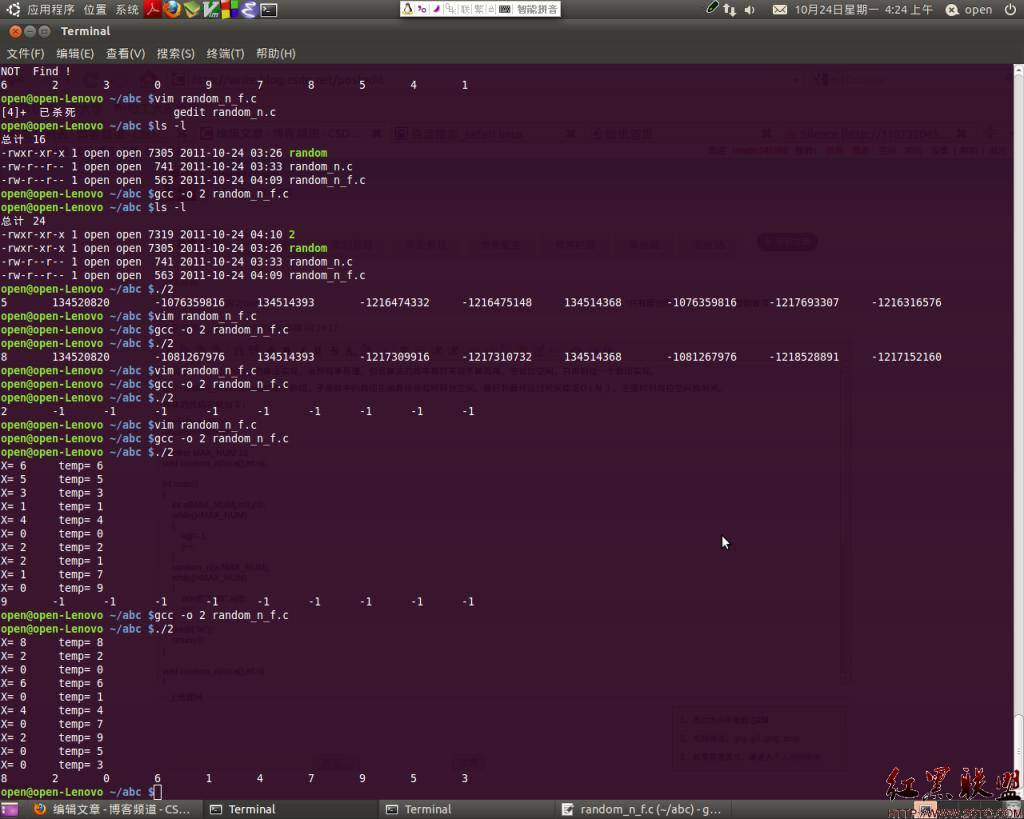
主要的思想:先產生0-N 之間的所有數,然後依次產生一個隨機數,把產生的隨機數當做下標,訪問已經產生的有序數組,並取出下表所對應的值付給我們傳進來的元數組。然後把這個數用最後一個數據覆蓋掉。然後讓產生隨機數的模減1,這樣下次訪問的有效范圍便是之前沒有訪問過的。這樣依次循環進行知道數組填滿。
思考過程如下:
----------------------------------------------------------------------------------------------
| 0 | 1 | 2 | .。。。 | 。。。 | N-1 | N |
-----------------------------------------------------------------------------------------------
假如產生的隨機數為2,則:
----------------------------------------------------------------------------------------------
| 0 | 1 | N | .。。。 | 。。。 | N-1 | N |
-----------------------------------------------------------------------------------------------
下一次的尋址范圍是:
----------------------------------------------------------------------------------------------
| 0 | 1 | 2 | .。。。 | 。。。 | N-1 | N |
-----------------------------------------------------------------------------------------------
依次覆蓋。
摘自 明月天涯