請注意,為了能夠更好的理解二叉排序樹,我建議各位在看代碼時能夠設置好斷點一步一步跟蹤函數的運行過程以及各個變量的變化情況
在進行動態查找操作時,如果我們是在一個無序的線性表中進行查找,在插入時可以將其插入表尾,表長加1即可;刪除時,可以將待刪除元素與表尾元素做個交換,表長減1即可。反正是無序的,當然是怎麼高效怎麼操作。但如果是有序的呢?回想學習線性表順序存儲時介紹的順序表的缺點,就在於插入刪除操作的復雜與低效。
正因為如此,我們引入了鏈式存儲結構,似乎這樣就能解決上面遇到的問題了。但細想一下,我們要進行的是查找操作,而鏈式結構的好處在於插入刪除,但在查找方面則顯得無能為力。那麼有沒有一種結構能讓我們既提高查找的效率,又不影響插入刪除的效率呢?
先從最簡單的情況考慮,我們現在有一個只有一個數據元素的集合,假設為{20},現在我需要查找其中是否含有’56’這個數字,沒有則插入;那麼很顯然執行該操作後集合變成了{20,56},繼續查找集合中是否有’16’這個元素,沒有則插入並且不改變原先的有序性。似乎要插入新數據就必須做移動。有沒有辦法不移動呢?有人想到了用二叉樹來存儲數據,讓20做根節點,56比20大所以做右子樹,16比20小所以做左子樹,這樣不就不用移動其位置了嗎?思路見下圖
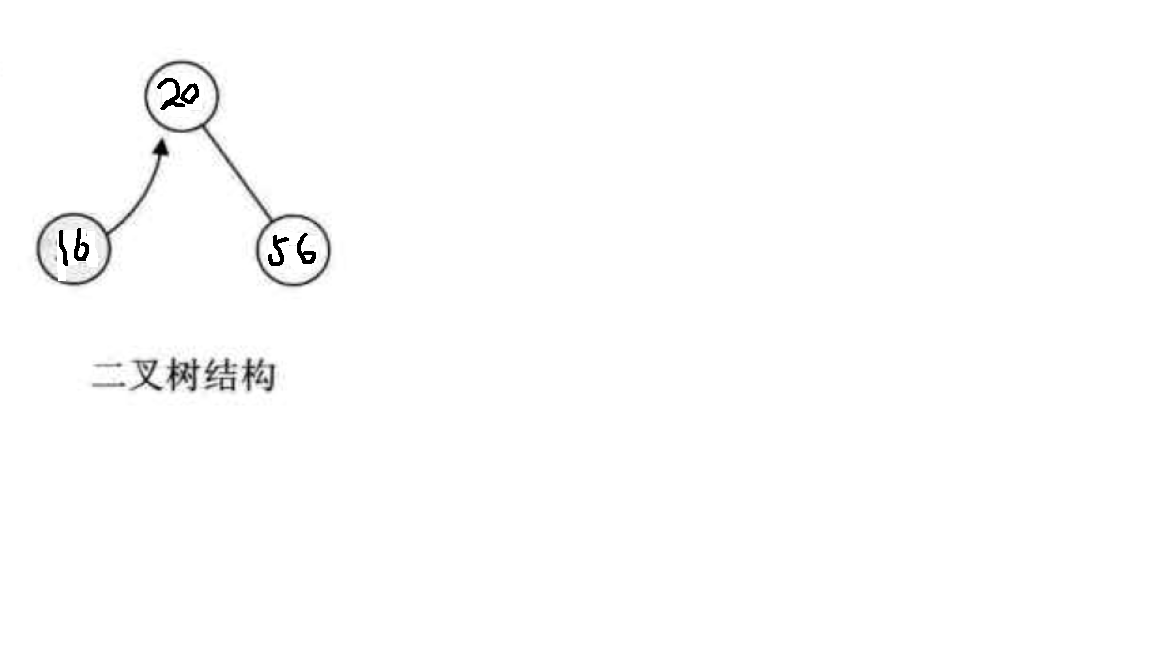
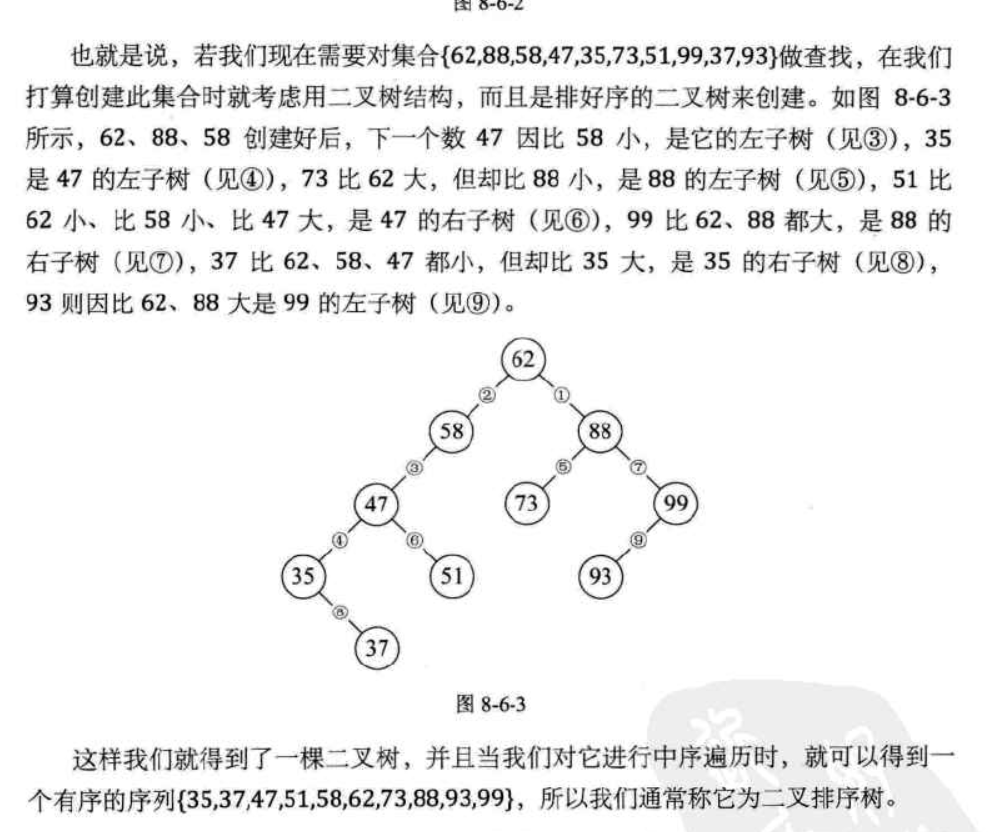
二叉排序樹或者是一棵空樹,或者是一棵有下列性質的二叉樹:
1.若它的左子樹不為空,則它左子樹上所有結點的值必然小於根結點的值
2.若它的右子樹不為空,則它右子樹上所有結點的值必然大於根結點的值
3.它的左右子樹也為二叉排序樹
之所以要構造這樣一棵樹,不是為了排序,而是為了提高查找,插入和刪除的效率
要構建一棵二叉排序樹並實現相關操作,首先應理解下列的三個操作
/*在BST中查找值為key的元素,f為指向雙親的指針,p用來返回查找路徑上最後一個結點*/
Status SearchBST(BiTree T,int key,BiTree f,BiTree *p){
if(!T){
*p=f;
return ERROR;
}
if(T->data==key){
*p=T;
return OK;
}
else{
/*如果key值小於當前值,則進入左子樹中查找*/
if(keydata)
return SearchBST(T->Lchild,key,T,p);/*注意這裡,遞歸調用的時候其雙親結點f應該為T*/
else
return SearchBST(T->Rchild,key,T,p);
}
}
要進行插入,首先要在BST中進行查找,若key值已經存在,則應返回ERROR;不存在時,由於第一步的search操作已經返回了查找路徑上的最後一個結點,只需要把key值與最後一個節點的值進行比較,比它小則為左子樹,反之為右子樹,代碼如下:
/*查找key是否存在於BST中,如果不存在,則插入key到合適位置*/
Status InsertBST(BiTree *T,int key){
/*found用於返回其查找過程中最後一個結點,insert為指向待插入結點的指針*/
BiTree found=NULL,insert=NULL;
/*沒找到*/
if(!SearchBST(*T,key,NULL,&found)){
insert=(BiTree)malloc(sizeof(BiTreeNode));
if(!insert){
printf("malloc failed\n");
return ERROR;
}
insert->data=key;
insert->Lchild=NULL;
insert->Rchild=NULL;
// if(*T==found)
/*如果found空,說明根節點值應為key*/
if(!found)
*T=insert;
else{
/*key值小於上一節點的data時,做左子樹*/
if(keydata)
found->Lchild=insert;
if(key>found->data)
found->Rchild=insert;
}
}
/*如果找到了,返回ERROR*/
else
return ERROR;
}
由於二叉排序樹具有比二叉樹更多的特性,所以刪除操作就變得更復雜,不能因為刪除一個結點導致整棵樹不滿足BST的性質。所以應該分三種情況進行討論:
1.刪除的是葉子節點
2.刪除的是只有左子樹或右子樹的節點
3.刪除的結點既有左子樹也有右子樹
對於第一種情況,直接刪除即可,葉子結點對整棵樹的性質並沒有影響
對於第二種情況,只有左或右子樹,只需要讓待刪除結點的指針指向其子樹即可,同時釋放原根結點指針即可
對於既有左子樹又有右子樹的情況,就比較復雜了,如圖所示:要刪除下圖中的值為47的節點,並且還要保持其是一棵BST,如何解決呢?
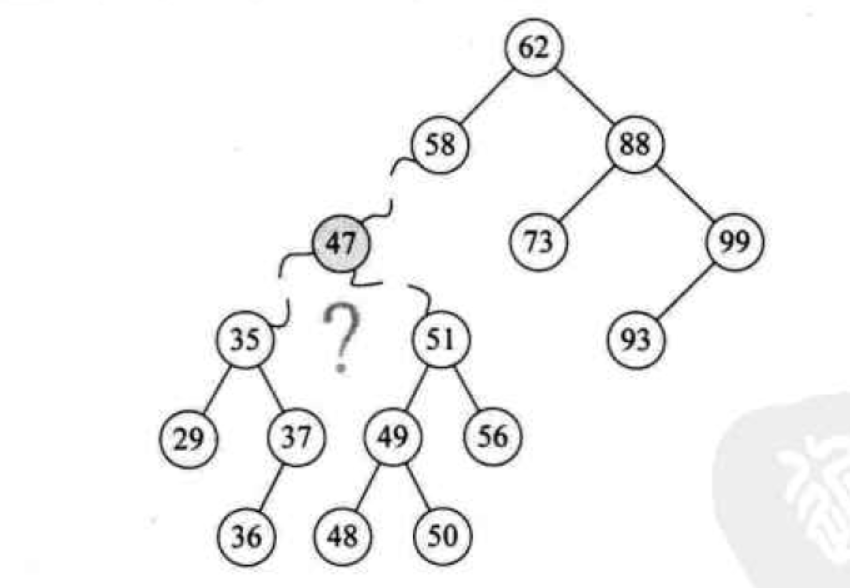 vcu8v7yjrDM3us00OMTcubvM5rT6NDe1xNSt0vLU2tPaOrWxztLDx9bQ0PKx6cD60tQ0N86quPm1xLb+subK98qxo6wzN7rNNDjKxzQ3tcTWsb3Tx7DH/brNuvO8zKGj1eLR+c7Sw8e+zbXDtb3By9K7uPa94cLbo6zJvrP9stnX98qxo6y0/cm+s/294bXj1NrW0NDysenA+rXE1rG908ewx/278rrzvMy/ydLUzOa0+sbkzrvWw6GjxeTNvNK71cXLtcP3y7zCtzo8L3A+DQo8cD48aW1nIGFsdD0="這裡寫圖片描述" src="/uploadfile/Collfiles/20160601/20160601094000582.png" title="\" />
vcu8v7yjrDM3us00OMTcubvM5rT6NDe1xNSt0vLU2tPaOrWxztLDx9bQ0PKx6cD60tQ0N86quPm1xLb+subK98qxo6wzN7rNNDjKxzQ3tcTWsb3Tx7DH/brNuvO8zKGj1eLR+c7Sw8e+zbXDtb3By9K7uPa94cLbo6zJvrP9stnX98qxo6y0/cm+s/294bXj1NrW0NDysenA+rXE1rG908ewx/278rrzvMy/ydLUzOa0+sbkzrvWw6GjxeTNvNK71cXLtcP3y7zCtzo8L3A+DQo8cD48aW1nIGFsdD0="這裡寫圖片描述" src="/uploadfile/Collfiles/20160601/20160601094000582.png" title="\" />
看了圖片可能覺得思路清晰一些了,下面看代碼吧:
/*刪除BST中某一結點,並重接其左右子樹*/
Status Delete(BiTree *T){
BiTree qmove=NULL,smove=NULL;
if(!(*T))
return ERROR;
/*如果只有右子樹*/
if((*T)->Lchild==NULL){
qmove=*T;/*用qmove保存待刪除結點*/
(*T)=(*T)->Rchild;/*待刪除結點指向其右子樹*/
free(qmove);
}
/*這裡要注意一定要寫成else if,否則會出現錯誤*/
else if((*T)->Rchild==NULL){
qmove=*T;
(*T)=(*T)->Lchild;
free(qmove);
}
else{
qmove=*T;
/*先左轉再右轉至指針為空是為了找到其中序遍歷的直接前驅*/
smove=(*T)->Lchild;
while(smove->Rchild){
qmove=smove;
smove=smove->Rchild;
}
/*smove指向待刪除結點的直接前驅*/
(*T)->data=smove->data;/*首先把smove指向的值賦給待刪除結點,下一步要做的是刪除smove並且把smove的孩子結點接好*/
if(qmove!=(*T))/*如果qmove不指向待刪除結點,則把smove的左子樹賦給qmove的右子樹*/
qmove->Rchild=smove->Lchild;
else
qmove->Lchild=smove->Lchild;/*否則把smove的左子樹賦給qmove的左子樹*/
free(smove);
}
return OK;
}
/*查找BST中是否存在key,若存在則刪除key*/
Status DeleteBST(BiTree *T,int key){
if(!(*T))
return ERROR;
else{
if((*T)->data==key)
Delete(T);
else if(key<(*T)->data)
DeleteBST(&(*T)->Lchild,key);
else if(key>(*T)->data)
DeleteBST(&(*T)->Rchild,key);
}
}
/*此處順便附上主程序*/
int main(void)
{
int i;
int a[10]={62,88,58,47,35,73,51,99,37,93};
BiTree T=NULL,p;
for(i=0;i<10;i++)
{
InsertBST(&T, a[i]);
}
DeleteBST(&T,93);
DeleteBST(&T,47);
Inorder(T);//中序遍歷
// SearchBST(T,35,NULL,&p);
// printf("%d",p->data);
return 0;
}
前兩種情況比較簡單,不再贅述,下面分析第三種情況
第一步:聲明兩個指針,qmove指向待刪除結點,smove指向待刪除結點的左子樹之後讓smove往右子樹移動,同時qmove記錄smove的位置,這一步是為了找到待刪除結點的直接前驅
第二步:將smove的值賦給根節點,如果這時qmove沒有指向根結點,則讓qmove的右子樹指向smove的左子樹;否則qmove的左子樹指向smove的左子樹
第三步,釋放smove
下面這組圖片展示了這段代碼運行時的每一步的狀態:
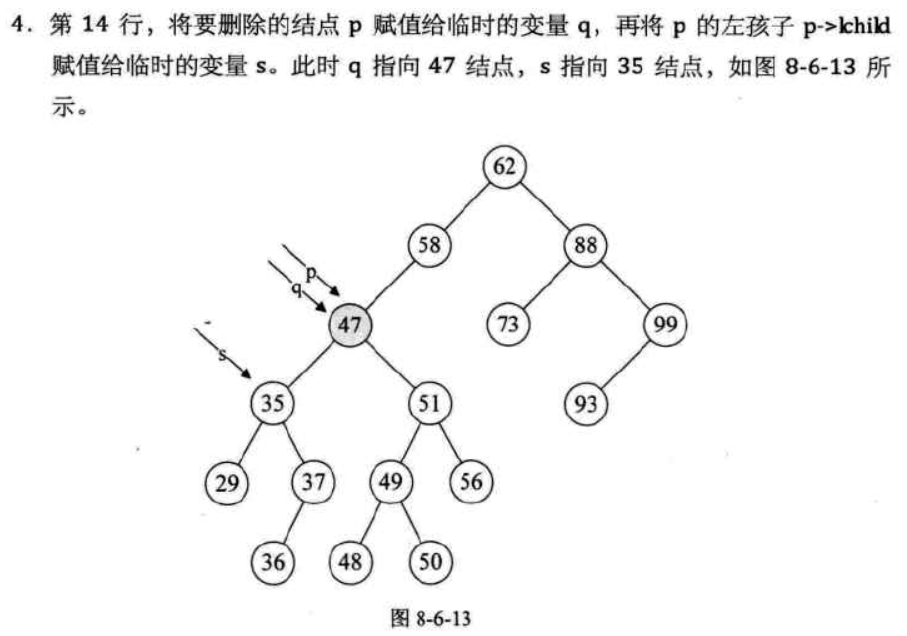
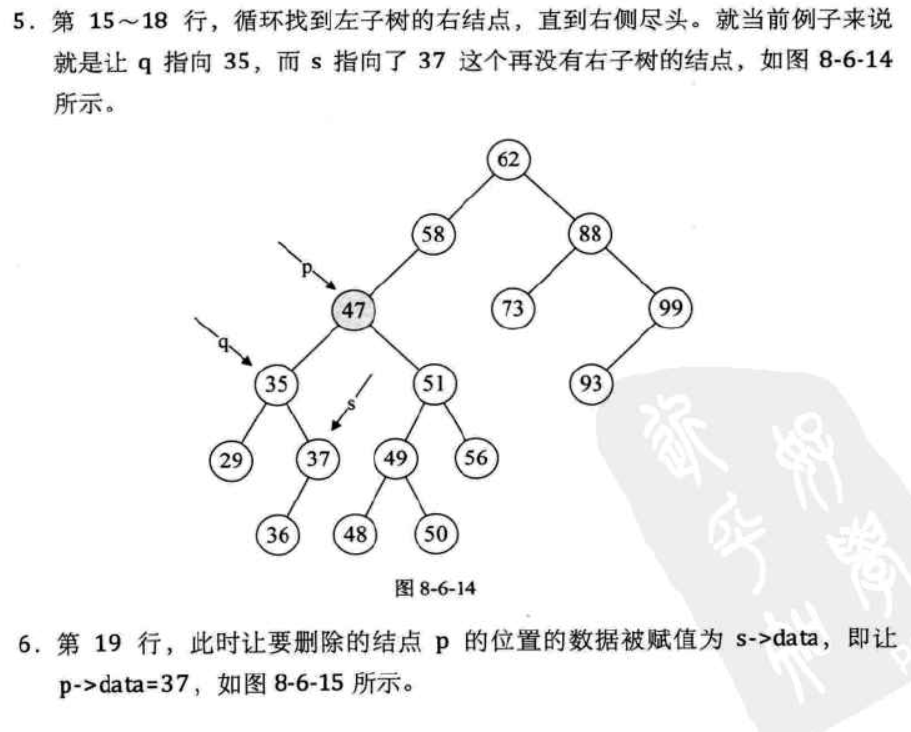
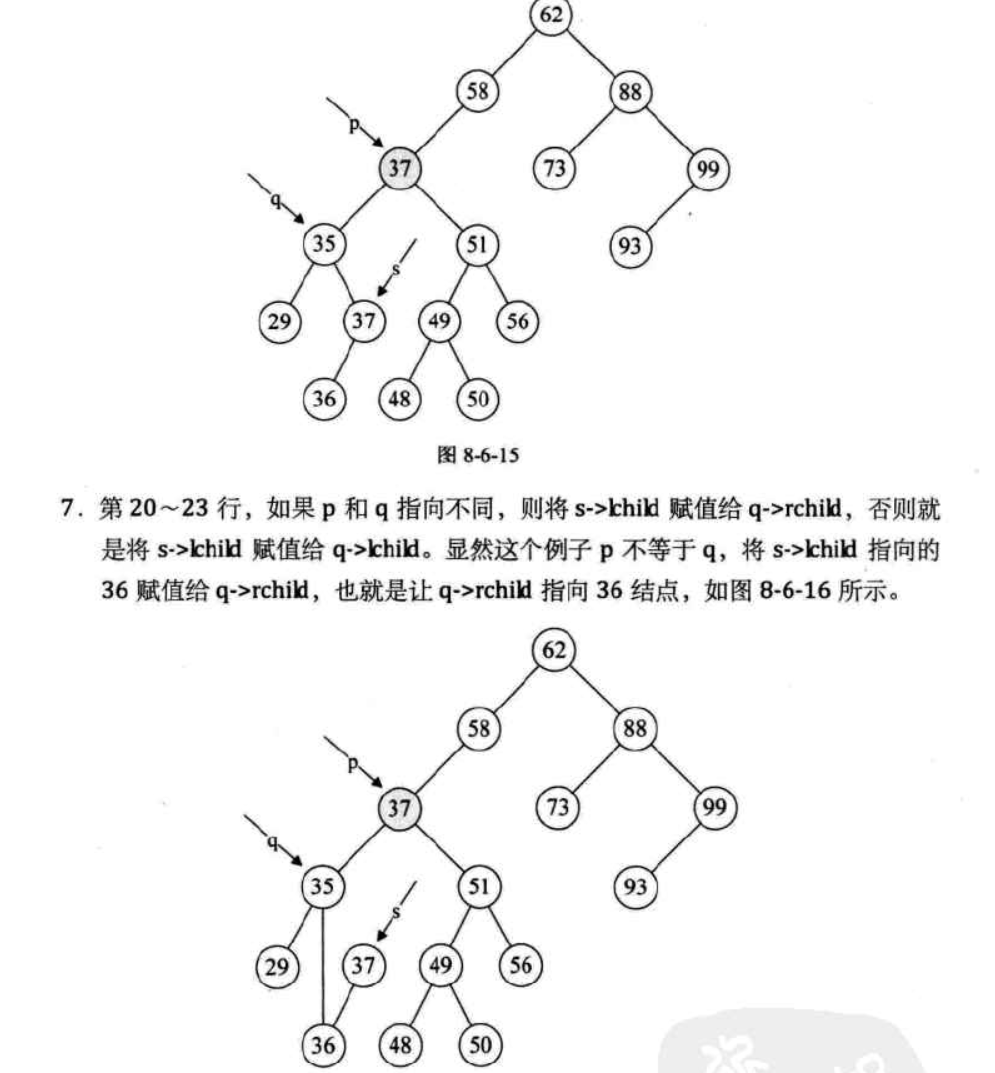
至此,刪除操作才算告一段落
二叉排序樹采用鏈式存儲,有較好的插入刪除的時間性能;查找方面,最好情況是1次找到,最差情況也不會超過樹的深度。因此,查找方面的性能取決於輸的形狀,比如有下面這樣的兩棵樹:
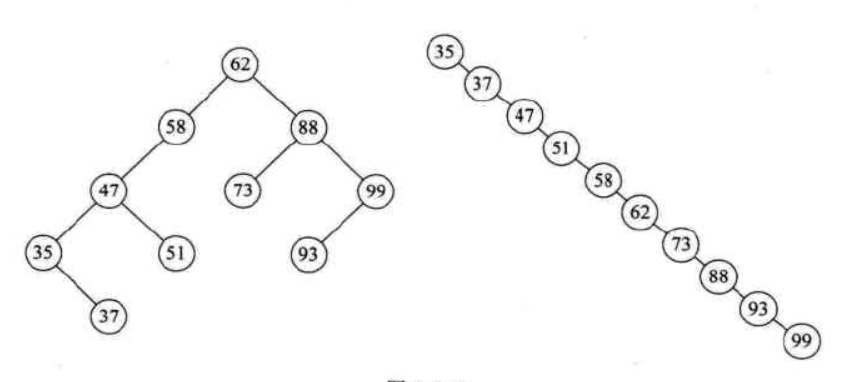
兩棵樹的數據全部相同,注意右邊的樹也是二叉排序樹,只不過其元素由於是從小到大排列的導致成了一棵右斜樹,要查找99這個元素,左邊的樹只需要兩次比較,而右邊要 10次比較,差異非常大,已經失去了二叉排序樹的意義,因此,如何讓二叉樹兩邊變得均衡一些,是我們下一個需要研究的問題。