上一節我們總體介紹項目並說明Minst手寫數字數據庫的使用,這一節我們將重點介紹CNN網絡總體結構。
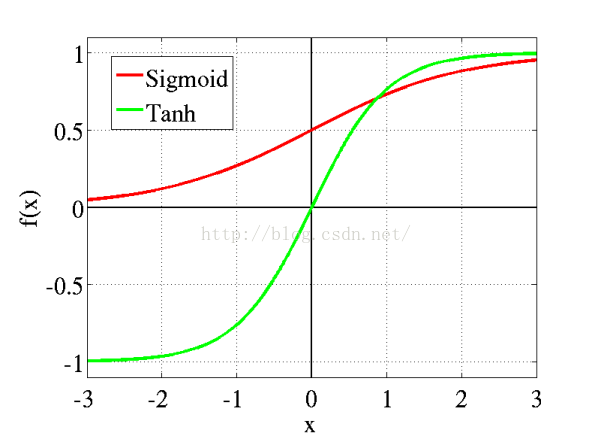
上圖我們已經非常熟悉,其為Yann在1998年介紹的LeNet-5網絡的結構,其剛被提出,就在學術和工業領域上得到廣泛應用,而本文的CNN卷積網絡卻是如下圖所示(博主自己畫的,畫這個圖還是挺麻煩的:L,不清晰請原諒),和LeNet-5相比主要有以下三點不同:
(1)LeNet-5給輸入圖像增加了一圈黑邊,使輸入圖像大小變成了32x32,這樣的目的是為了在下層卷積過程中保留更多原圖的信息。
(2)LeNet-5的卷積層C3只有16個模板,得到16個輸出,而本文的卷積層C3由於是全連接,所以有6*12個模板,得到12個輸出圖像
(3)LeNet-5多了兩種,分別是C5到F6的全連接神經網絡層,和F6到OUTPUT高斯連接網絡層。而本文的直接由采樣層S4直接經過一層全連接神經網絡層到OUTPUT。
下面我們將重點介紹各層的結構及數據的前向傳播。
一、各層的解釋
(1)卷積層C1
輸入為28x28的灰度圖像,灰度圖像分別同6個5x5的模板進行卷積操作,分別得到了6個24x24的卷積圖像,圖像裡的每個像素加上一個權重,並經過一個激活函數,得到該層的輸出。
所以該層的相關參數為:6個5x5的模板參數w,6個模板對應的權重參數b,共6x5x5+6個參數
Tips:
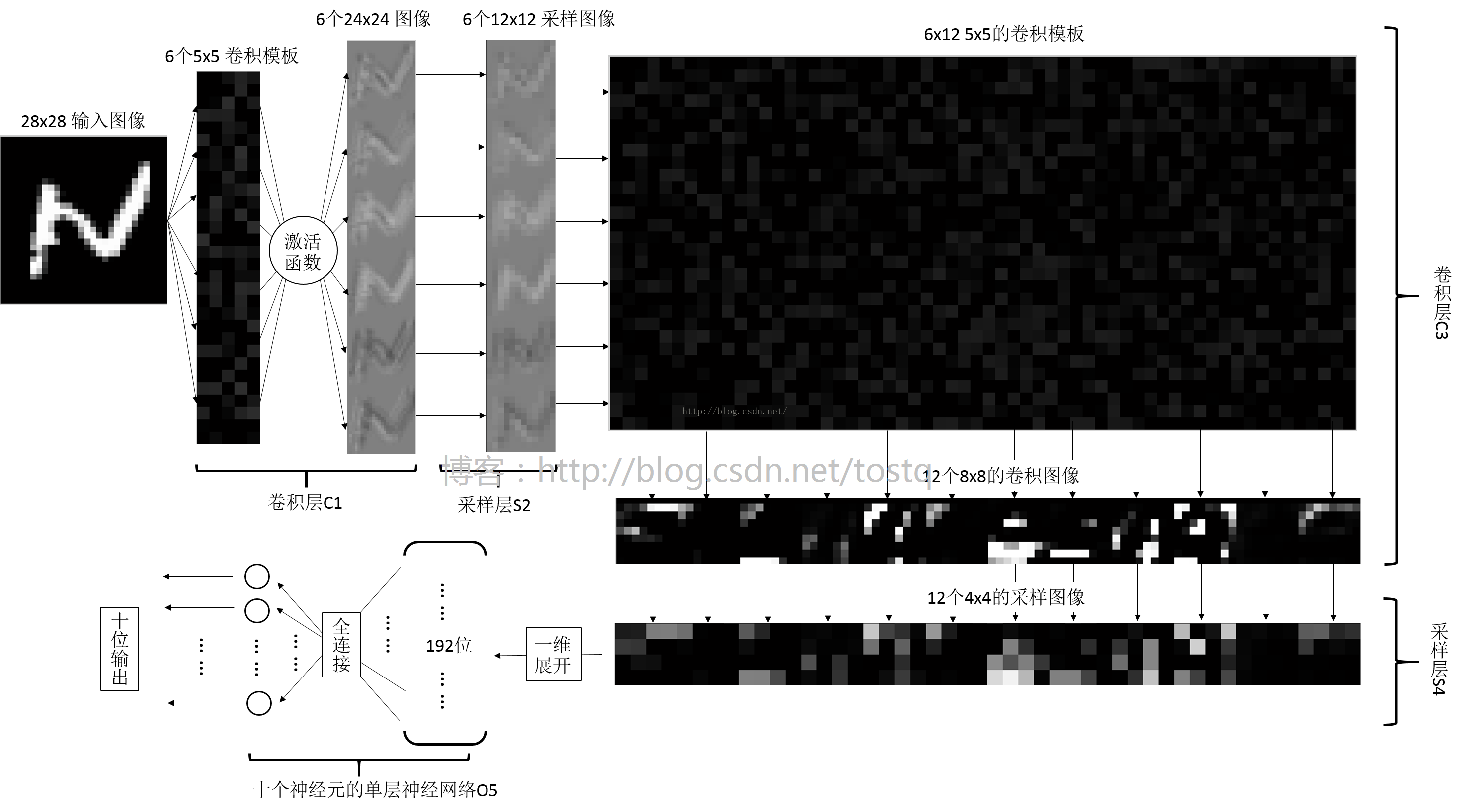
關於激活函數:激活函數我們在學習神經網絡時就已經接觸過了,其主要有兩個目的,第一是將數據鉗制在一定范圍內(如Sigmoid函數將數據壓縮在-1到1之間),不太高也不太低,第二是用來加入非線性因素的,因為線性模型的表達能力不夠。傳統神經網絡中最常用的兩個激活函數Sigmoid系和Tanh系,而Sigmoid系(Logistic-Sigmoid、Tanh-Sigmoid)被視為神經網絡的核心所在。本文的例子就是Sigmoid系。

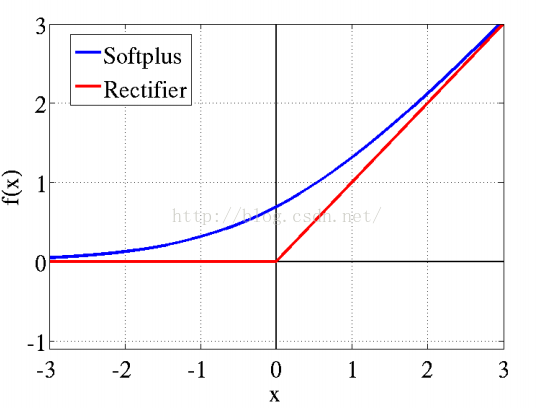
近年來,在深度學習領域中效果最好,應用更為廣泛的是ReLu激活函數,其相較於Sigmoid系,主要變化有三點:①單側抑制 ②相對寬闊的興奮邊界 ③稀疏激活性。特別是在神經科學方面,除了新的激活頻率函數之外,神經科學家還發現了的稀疏激活性廣泛存在於大腦的神經元,神經元編碼工作方式具有稀疏性和分布性。大腦同時被激活的神經元只有1~4%。從信號方面來看,即神經元同時只對輸入信號的少部分選擇性響應,大量信號被刻意的屏蔽了,這樣可以提高學習的精度,更好更快地提取稀疏特征。而在經驗規則的初始化W之後,傳統的Sigmoid系函數同時近乎有一半的神經元被激活,這不符合神經科學的研究,而且會給深度網絡訓練帶來巨大問題。Softplus照顧到了新模型的前兩點,卻沒有稀疏激活性。因而,校正函數max(0,x)即ReLu函數成了最大贏家。
(2)采樣層S2及S4(Pooling層)
采樣層S又名Pooling層,Pooling主要是為了減少數據處理的維度,常見的pooling方法有max pooling和average pooling等。
max pooling 就是選擇當前塊內最大像素值來表示當前局部塊
average pooling 就是選擇當前塊的像素值平均值來代替
本文的選擇Pooling方法是average pooling,而使用廣泛效果較好的方法卻是max pooling。(看到這裡,你可能會吐槽,為什麼不用效果好,因為平均計算相比而言,有那麼一丟丟簡單!)
(3)卷積層C3
這裡的卷積層是一個全連接的卷積層。輸出的卷積公式如下,這裡I表示圖像,W表示卷積模板,b表示偏重,φ表示激活函數,i表示輸入圖像序號(i=1~6),j表示該層輸出圖像序號(j=1~12)
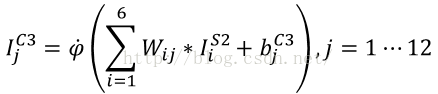
由此可以看到在卷積層C3中輸入為6個12x12的圖像,輸出為12個8x8的圖像
所需要訓練的參數有6x12個5x5的卷積模板w和12個偏重b(每個模板對應的偏重都是相同的)
而實際上由於神經網絡的稀疏結構和減少訓練時間的需要,該卷積層一般不是利用全連接的,就比如前面介紹LeNet-5網絡,只需要利用16個卷積模板就可以了,而不是全連接的6x12個,其連接方法如下,其最終得到16個輸出圖像。
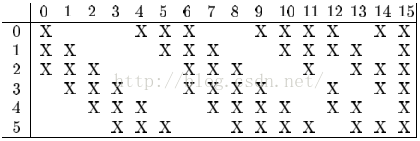
這裡X表示選擇卷積,比如第0張輸出圖像是由第0、1、2張輸入圖像分別同第0個卷積模板卷積相加,再加上偏重,經過激活函數得到的。而第15張圖像是由第0、1、2、3、4、5張輸入圖像分別同第15個卷積模板卷積相加得到的。
(4)輸出層O5:
采樣層S4後,我們將得到12張4*4的圖像,將所有圖像展開成一維,就得到了12*4*4=192位的向量。
輸出層是由輸入192位,輸出10位的全連接單層神經網絡,共有10個神經元構成,每個神經元都同192位輸入相連,即都有192位的輸入和1位輸出,其處理公式如下,這裡j表示輸出神經元的序號,i表示輸入的序號。
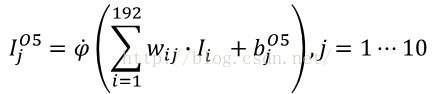
所以該層參數共有192*10個權重w,和10個偏重b
二、卷積神經網絡的相關數據結構
這個卷積網絡主要有五層網絡,主要結構是卷積層、采樣層(Pooling)、卷積層、采樣層(Pooling)和全連接的單層神經網絡層(輸出層),所以我們建立了三個基本層的結構及一個總的卷積網絡結構。
這裡結構內除了必要的權重參數,而需要記錄該層輸入輸出數據y,及需要傳遞到下一層的局部梯度d。
(1)卷積層
// 卷積層
typedef struct convolutional_layer{
int inputWidth; //輸入圖像的寬
int inputHeight; //輸入圖像的長
int mapSize; //特征模板的大小,模板一般都是正方形
int inChannels; //輸入圖像的數目
int outChannels; //輸出圖像的數目
// 關於特征模板的權重分布,這裡是一個四維數組
// 其大小為inChannels*outChannels*mapSize*mapSize大小
// 這裡用四維數組,主要是為了表現全連接的形式,實際上卷積層並沒有用到全連接的形式
// 這裡的例子是DeapLearningToolboox裡的CNN例子,其用到就是全連接
float**** mapData; //存放特征模塊的數據
float**** dmapData; //存放特征模塊的數據的局部梯度
float* basicData; //偏置,偏置的大小,為outChannels
bool isFullConnect; //是否為全連接
bool* connectModel; //連接模式(默認為全連接)
// 下面三者的大小同輸出的維度相同
float*** v; // 進入激活函數的輸入值
float*** y; // 激活函數後神經元的輸出
// 輸出像素的局部梯度
float*** d; // 網絡的局部梯度,δ值
}CovLayer;
(2)采樣層
// 采樣層 pooling
typedef struct pooling_layer{
int inputWidth; //輸入圖像的寬
int inputHeight; //輸入圖像的長
int mapSize; //特征模板的大小
int inChannels; //輸入圖像的數目
int outChannels; //輸出圖像的數目
int poolType; //Pooling的方法
float* basicData; //偏置
float*** y; // 采樣函數後神經元的輸出,無激活函數
float*** d; // 網絡的局部梯度,δ值
}PoolLayer;
(3)全連接的單層神經網絡
// 輸出層 全連接的神經網絡
typedef struct nn_layer{
int inputNum; //輸入數據的數目
int outputNum; //輸出數據的數目
float** wData; // 權重數據,為一個inputNum*outputNum大小
float* basicData; //偏置,大小為outputNum大小
// 下面三者的大小同輸出的維度相同
float* v; // 進入激活函數的輸入值
float* y; // 激活函數後神經元的輸出
float* d; // 網絡的局部梯度,δ值
bool isFullConnect; //是否為全連接
}OutLayer;
(4)各層共同組成一個完整的卷積網絡
typedef struct cnn_network{
int layerNum;
CovLayer* C1;
PoolLayer* S2;
CovLayer* C3;
PoolLayer* S4;
OutLayer* O5;
float* e; // 訓練誤差
float* L; // 瞬時誤差能量
}CNN;
(5)另外還有一個用於存放訓練參量的結構
typedef struct train_opts{
int numepochs; // 訓練的迭代次數
float alpha; // 學習速率
}CNNOpts;
三、卷積神經網絡的初始化
卷積神經網絡的初始化主要包含了各數據的空間初始化及權重的隨機賦值,沒有什麼復雜,按照結構分配空間就可以了,這裡不再詳細贅述了,可以直接參考代碼內cnnsetup()函數
四、卷積神經網絡的前向傳播過程
前向傳播過程實際上就是指輸入圖像數據,得到輸出結果的過程,而後向傳播過程就是將輸出結果的誤差由後向前傳遞給各層,各層依次調整權重的過程。所以前向傳播過程相比而是比較直觀,而且簡單的。
前向傳播過程在項目中主要是由cnnff函數完成,下面我們將按層介紹其過程
(1)卷積層C1
卷積層C1共有6個卷積模板,每個模板同輸入圖像卷積將會得到一個輸出,即共6個輸出,以下是圖像的卷積公式:
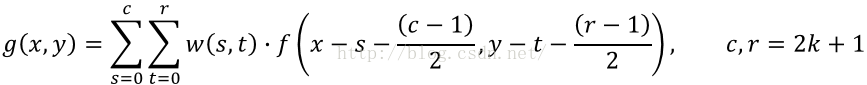
C1層的相關代碼,這裡cov函數是卷積函數,在mat.cpp是具體的定義,activation_Sigma是激活函數
int outSizeW=cnn->S2->inputWidth;
int outSizeH=cnn->S2->inputHeight;
// 第一層的傳播
int i,j,r,c;
// 第一層輸出數據
nSize mapSize={cnn->C1->mapSize,cnn->C1->mapSize};
nSize inSize={cnn->C1->inputWidth,cnn->C1->inputHeight};
nSize outSize={cnn->S2->inputWidth,cnn->S2->inputHeight};
for(i=0;i<(cnn->C1->outChannels);i++){
for(j=0;j<(cnn->C1->inChannels);j++){
float** mapout=cov(cnn->C1->mapData[j][i],mapSize,inputData,inSize,valid);
addmat(cnn->C1->v[i],cnn->C1->v[i],outSize,mapout,outSize);
for(r=0;rC1->y[i][r][c]=activation_Sigma(cnn->C1->v[i][r][c],cnn->C1->basicData[i]);
}
(2)采樣層S2,avgPooling是平均Pooling函數
// 第二層的輸出傳播S2,采樣層
outSize.c=cnn->C3->inputWidth;
outSize.r=cnn->C3->inputHeight;
inSize.c=cnn->S2->inputWidth;
inSize.r=cnn->S2->inputHeight;
for(i=0;i<(cnn->S2->outChannels);i++){
if(cnn->S2->poolType==AvePool)
avgPooling(cnn->S2->y[i],outSize,cnn->C1->y[i],inSize,cnn->S2->mapSize);
}
(3)卷積層C3,同C1很類似
// 第三層輸出傳播,這裡是全連接
outSize.c=cnn->S4->inputWidth;
outSize.r=cnn->S4->inputHeight;
inSize.c=cnn->C3->inputWidth;
inSize.r=cnn->C3->inputHeight;
mapSize.c=cnn->C3->mapSize;
mapSize.r=cnn->C3->mapSize;
for(i=0;i<(cnn->C3->outChannels);i++){
for(j=0;j<(cnn->C3->inChannels);j++){
float** mapout=cov(cnn->C3->mapData[j][i],mapSize,cnn->S2->y[j],inSize,valid);
addmat(cnn->C3->v[i],cnn->C3->v[i],outSize,mapout,outSize);
for(r=0;rC3->y[i][r][c]=activation_Sigma(cnn->C3->v[i][r][c],cnn->C3->basicData[i]);
}
(4)采樣層S4,同S2很類似
// 第四層的輸出傳播
inSize.c=cnn->S4->inputWidth;
inSize.r=cnn->S4->inputHeight;
outSize.c=inSize.c/cnn->S4->mapSize;
outSize.r=inSize.r/cnn->S4->mapSize;
for(i=0;i<(cnn->S4->outChannels);i++){
if(cnn->S4->poolType==AvePool)
avgPooling(cnn->S4->y[i],outSize,cnn->C3->y[i],inSize,cnn->S4->mapSize);
}
(5)輸出層O5
// 輸出層O5的處理
// 首先需要將前面的多維輸出展開成一維向量
float* O5inData=(float*)malloc((cnn->O5->inputNum)*sizeof(float));
for(i=0;i<(cnn->S4->outChannels);i++)
for(r=0;rS4->y[i][r][c];
nSize nnSize={cnn->O5->inputNum,cnn->O5->outputNum};
nnff(cnn->O5->v,O5inData,cnn->O5->wData,cnn->O5->basicData,nnSize);
for(i=0;iO5->outputNum;i++)
cnn->O5->y[i]=activation_Sigma(cnn->O5->v[i],cnn->O5->basicData[i]);
free(O5inData);
}