一.理論分析
Shannon-Fano-Elias編碼是利用累積分布函數來分配碼字。
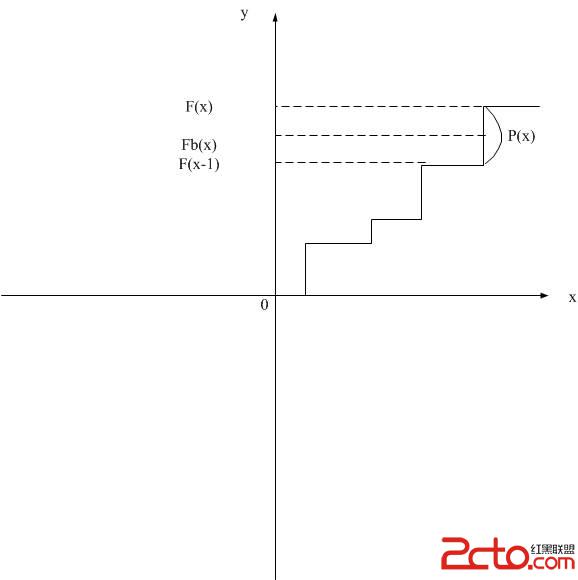
不失一般性,假定取X={1,2,…m}。假設對於所有的x,有p(x)>0。定義累積分布函數F(X)為 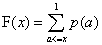
其函數圖形見下圖所示,修正的累積分布函數為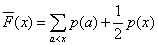 其中
其中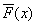 表示小於x的所有字符的概率和加上字符x概率的一般得到的值。由於隨機變量是離散的,故累積分布函數所含的階梯高度為p(x)。函數
表示小於x的所有字符的概率和加上字符x概率的一般得到的值。由於隨機變量是離散的,故累積分布函數所含的階梯高度為p(x)。函數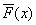 的值恰好與x對應的那個階梯的中點。
的值恰好與x對應的那個階梯的中點。
我們現在要確定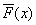 vc/g06a1xHiho9LyzqrL+dPQtcS4xcLK1rW++c6q1f3WtaOsyPQ8aW1nIGFsdD0="6" src="/uploadfile/Collfiles/20160416/20160416091815735.gif" title="\" />則
vc/g06a1xHiho9LyzqrL+dPQtcS4xcLK1rW++c6q1f3WtaOsyPQ8aW1nIGFsdD0="6" src="/uploadfile/Collfiles/20160416/20160416091815735.gif" title="\" />則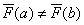 因此通過累積分布函數就可以得到相應的X。但一般情況下
因此通過累積分布函數就可以得到相應的X。但一般情況下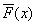 為十進制小數,要表示為二進制小數需要很多比特位,(在編碼實現的過程中要注意此處,若是C語言實現,要注意存儲二進制比特位的數組的長度,此處極易發生數組越界)這在現實的編碼中是並不可行的。因此我們需要取一個精度,到底精確到哪一位呢?
為十進制小數,要表示為二進制小數需要很多比特位,(在編碼實現的過程中要注意此處,若是C語言實現,要注意存儲二進制比特位的數組的長度,此處極易發生數組越界)這在現實的編碼中是並不可行的。因此我們需要取一個精度,到底精確到哪一位呢?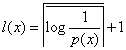 取到l(x)位即可。
取到l(x)位即可。
二.編碼實現
Shannon-Fano-Elias編碼是用C語言來實現的。
code數組的長度建議定的大一些,此處極易發生數組越界(這都是血的教訓啊….)
基本的結構體如下:
typedef struct
{
double px; //px概率值
double Fx; //fx函數值
double Fbax; //Fba(X)的值
int lx; //編碼的長度
int code[A]; //存儲二進制比特
}SFE;
1.初始化結構體,輸入p(x)
void init_code(int code[],int i)
{
int j;
for (j=0;j
2.計算fx累積分布函數
void count_fx(SFE SFEA[],int length)//計算fx累積分布函數
{
double sum =0;
int i,j;
for (i=1;i<=length;i++)
{
for (j=1;j<=i;j++)
{
sum = sum + SFEA[j].px;
}
SFEA[i].Fx = sum;
sum = 0;
}
}
3.計算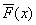
void count_fbax(SFE SFEA[],int length)//計算fbax的函數值
{
int i,j;
double sum = 0;
for (i=1;i<=length;i++)
{
if (i==1)
{
SFEA[i].Fbax = SFEA[i].px/2.0;
}
else
{
for (j=1;j
4.計算lx的長度,lx向上取整
void count_lx(SFE SFEA[],int length)//計算lx的長度,lx向上取整
{
int i;
for (i=1;i<=length;i++)
{
SFEA[i].lx = ceil(log(1/SFEA[i].px)/log(2))+1;
}
}
5.轉化為二進制比特位
void decimal(double m,int code[])
{
int *p = code;
if(m>ZERO)
{
m=m*NUM;
*p = (long)m;
p++;
decimal(m-(long)m,p);
}
}
void f_binary(SFE SFEA[],int length)
{
int i;
for (i=1;i<=length;i++)
{
decimal(SFEA[i].Fbax,SFEA[i].code);
}
}
整個編碼過程至此結束,因為數組操作比較多,所以要注意防止數組越界。
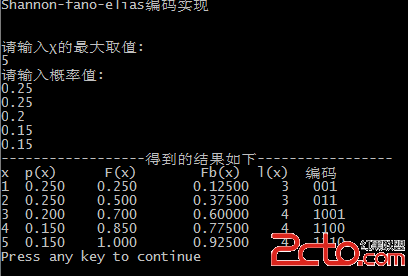
三.編碼結果分析
1.先給出一個例子,其十進制小數均可以轉化為有限位數的二進制小數。
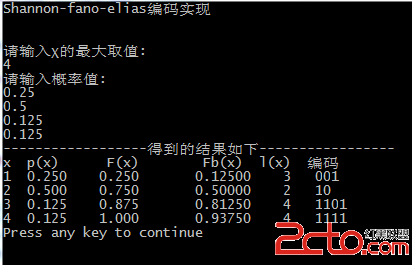
2.這個例子中二進制小數表示可能為無線位數的小數,開始的時候我將code數組的大小定義為20,執行完1中都很正常,到了這個例子,一直不停的發生數組越界,原因是因為,此例中二進制表示可能有無窮位數字。如果先轉化二進制,再編碼表示的話,code數組的長度要足夠長。當然,你也可以只存儲到l(x)位。這樣就不用那麼大的空間了。