
 更多內容請看C/C++技術專題 數據結構 數據結構教程專題,或
綜上,我們已經把這個問題解決了,可以看出,要害是如何確定當前柱需要移動多少盤子,這個問題請大家自己考慮,給出如下例程,因為沒有經過任何優化,本人的編碼水平又比較低,所以這個函數很慢——比遞歸的還慢10倍。
更多內容請看C/C++技術專題 數據結構 數據結構教程專題,或
綜上,我們已經把這個問題解決了,可以看出,要害是如何確定當前柱需要移動多少盤子,這個問題請大家自己考慮,給出如下例程,因為沒有經過任何優化,本人的編碼水平又比較低,所以這個函數很慢——比遞歸的還慢10倍。 更多內容請看C/C++技術專題 數據結構 數據結構教程專題,或
if (!m) { source = ns.pop(); target_m = ns.pop();
更多內容請看C/C++技術專題 數據結構 數據結構教程專題,或
if (!m) { source = ns.pop(); target_m = ns.pop(); 更多內容請看C/C++技術專題 數據結構 數據結構教程專題,或
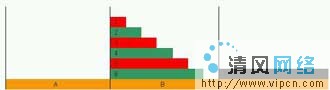
這個算法實現比遞歸算法復雜了很多(遞歸算法在網上、書上隨便都可以找到),而且還慢很多,似乎是多余的,然而,這是有現實意義的。
更多內容請看C/C++技術專題 數據結構 數據結構教程專題,或
這個算法實現比遞歸算法復雜了很多(遞歸算法在網上、書上隨便都可以找到),而且還慢很多,似乎是多余的,然而,這是有現實意義的。
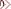 更多內容請看C/C++技術專題 數據結構 數據結構教程專題,或
更多內容請看C/C++技術專題 數據結構 數據結構教程專題,或