開發定點(fixed-point)算法時,通常需要在設計功能性、數字精度建模、及驗證(仿真)速度之間取得一個平衡。現在,一種新的數據類可使此過程簡單化,由此得到更簡單精確的建模精度、更好的數字求精、及更快的驗證周期,而ANSI C/C++正是開發這種數字求精算法的最佳語言。
某此算法天生就適用於操作整數,或那些理想中的實數(如數字濾波器的系數),它們也可能會使用浮點或定點類型。一般而言,在算法開發的早期階段,會經常用到C語言的float或double浮點類型,因為它們可提供一個非常大的動態數據范圍,且對大多數程序來說都是適用的。見圖1:
 使用C內置的float類型來建模一個FIR濾波器
使用C內置的float類型來建模一個FIR濾波器
算法可進行數字求精,以便使用定點算術來降低最終硬件或軟件實現的復雜性。在硬件方面,將整數或定點算術限制為最小位寬,可在本質上滿足性能、空間、能耗的需要;假如實現中用到了DSP處理器,那麼把算法限制為整數或定點算術,就可為特定程序使用盡可能便宜的處理器。
定點算術的建模可通過C語言內置的浮點或整數類型來完成,這做的話,需要顯式編碼並受限於C中浮點數及整數可表示的最大數:64位整數或53位尾數;這些都會給操作數的位寬帶來更多的限制,例如,2個33位的數相乘,會超過64位C整數可表示的范圍。圖2演示了一個FIR濾波器的例子,但temp變量限制為15位的定點精度,其中10位用於整數位。在這個實現中,LSB的右部位被捨棄(量化模型的截斷),而MSB的左部位也被捨棄(包裝的溢出模型),應該意識到,使用float(或double)的模型在精度上是受限的,且不能再次合成(synthesis)。同樣,由於有取整模型的嚴格位精度定義有先,又由於內置浮點類型的取整將會先被應用,所以對除法這樣的操作來說,就非常難實現了。
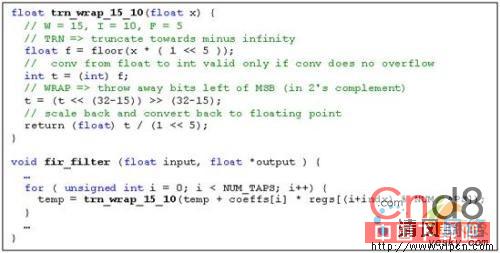 使用float建模定點行為
使用float建模定點行為
當許多算法都能依靠本地C數據類型的精度來編寫時,對支持任意長度的整數及定點算法,大家就會抱有極大的期望,而硬件描述語言(HDL)如VHDL,走的也是同一條路。隨著C/C++越來越多地被用於高級合成與驗證工具(High-Level Synthesis and Verification tools),也證實了這種語言本質上有一個足以滿足當前及未來程序需要的數據類型庫。任意長度類型的支持,也可使數據類型的行為有一個統一的定義,而統一的語義則避免了人工實現上的一些限制。
算法C數據類型
算法C數據類型是一種基於類的C++庫,其實現了任意長度的整數及定點類型,而這些可自由訪問的類型有一系列好處,包括統一及良好定義的語義,還有媲美C/C++內置數據類型的運行時速度,對比SystemC中相應的類型,其運行速度也超過10倍以上。這些數據類型能用於任何符合C++或SystemC規范標准的程序中,並擁有高度可合成的語義。
語義
語義的統一性與一致性是避免在算法中,發生功能性錯誤的要害,以下的例子,也說明了這點:
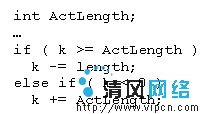
眾所周知,變量ActLength的范圍為1至255,萬一編譯器的合成不知道其范圍,就不能進行相應的優化,它的聲明就會從int變為更嚴格的sc_uint<8>類型;雖然合成會得到更好的結果,但設計就仿真得不正確了。在經過一番調試之後,找到了問題的源頭:在比較表達式k >= ActLength中,兩個操作數變成了一個signed int與一個unsigned long long(為64位無符號整數,其是sc_uint類型的基類型)之間的比較。對此的解釋是:C/C++整數提升規則指定了在進行比較之前,會把操作數int提升為一個unsigned long long,例如,假如k的值為 -1,在提升為unsigned long long之後,它會變成2^64 – 1。
像這樣語義中的問題一般會非常難以察覺,且是與位寬相關的,例如,可能有人想擴大某個現有算法的位寬,只有看到結果時,才知道是行不通的;這個問題也可能是與特定平台相關的,例如,對1 << 32(兩個操作數都是int類型,結果也是int類型)大家期望返回0,但在大多數平台(或編譯器)上,它都會返回1(沒有移位,只因為第二個操作數較低的五位被計算進來了);當第一個操作數是一個64位整數時,平台依靠性會表現得更加明顯及頻繁。主要的問題是C/C++標准沒有指定在32位整數情況下移位值(第二個操作數)超出0至31范圍、或在64位整數情況下移位值超出0至63范圍時的行為。不幸的是,像sc_int、sc_uint這樣的數據類型也不能為用戶避免這類平台依靠性的問題。
算法C數據類型被設計用於提供統一且一致的語義,因此,它們是可猜測的,例如,對有符號數混用一個無符號操作數仍會產生期望的結果;這些類型的長度不受限制,所以就不存在所謂的精度問題。所有的操作——包括移位和除法——都有完整且一致性的定義,混合不同的類型也能得到期望的結果,如,當x為一個C內置類型,而y是一個算法C類型時,表達式x+y和y+x均能返回相同的結果。
運行時間
我們的目的是為了在支持任意長度類型及避免用戶碰到前述語義問題的前提下,得到使用內置類型(位寬不超過64位)手工C/C++編碼優化過的運行時間。算法C類型是為快速執行及易於合成的語義而設計及實現的,所有操作的位寬由C++編譯器靜態確定,這就避免了動態內存分配,減少了運行時間,也使得語義更加易於合成。另外,實現也為速度進行了優化,因此可能會調用更多的專用及高效代碼,充分利用了當今編譯器的優化特性。
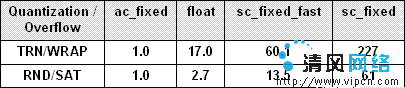
表1:規格化為ac_fixed的運行時間比較
表1是當定點算術用算法C定點類型ac_fixed來建模時,各種不同的運行時比較;float的實現在圖2中,sc_fixed_fast為SystemC中精度受限的定點數據類型,sc_fixed為任意精度的定點類型。實際中對FIR濾波器進行10^8次調用,TRN/WRAP的運行時間為6.5秒,RND/SAT為29秒。其他類型的運行時間也能從這張表中依次推出,如sc_fixed TRN/WRAP將花費6.5s × 227 = 1476s(將近25分鐘)。作為參考,圖1中的算法(使用無定點建模的float)花費時間為3.5s(比起使用定點建模的ac_fixed,慢了近兩倍)。
上述的運行時間數據,均由GCC 4.1.1測量得來,而在之前版本的GCC或Visual C++ 2005中得到的數據大致接近。
另外,運行時間也能通過整型數據類型或位操作進一步縮短。表2為一個DCT算法的相應結果,它由一個每次讀寫2位的移位操作得來,與此對比的運行時間為SystemC精度受限的sc_int與任意長度的sc_bigint。
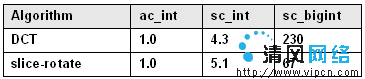
表2:規格化為ac_int的運行時間比較
結論
基於通用標准ANSI C++,這種新的整數與定點算法C類型答應算法及系統設計者指定任意位寬,從而提供比傳統數據類型高200倍的仿真效率。這些新數據類型可成為C-to-RTL設計鏈中非常有價值的一環,及在整個實現流程中保證了任意位寬的精度。
 使用C內置的float類型來建模一個FIR濾波器
算法可進行數字求精,以便使用定點算術來降低最終硬件或軟件實現的復雜性。在硬件方面,將整數或定點算術限制為最小位寬,可在本質上滿足性能、空間、能耗的需要;假如實現中用到了DSP處理器,那麼把算法限制為整數或定點算術,就可為特定程序使用盡可能便宜的處理器。
定點算術的建模可通過C語言內置的浮點或整數類型來完成,這做的話,需要顯式編碼並受限於C中浮點數及整數可表示的最大數:64位整數或53位尾數;這些都會給操作數的位寬帶來更多的限制,例如,2個33位的數相乘,會超過64位C整數可表示的范圍。圖2演示了一個FIR濾波器的例子,但temp變量限制為15位的定點精度,其中10位用於整數位。在這個實現中,LSB的右部位被捨棄(量化模型的截斷),而MSB的左部位也被捨棄(包裝的溢出模型),應該意識到,使用float(或double)的模型在精度上是受限的,且不能再次合成(synthesis)。同樣,由於有取整模型的嚴格位精度定義有先,又由於內置浮點類型的取整將會先被應用,所以對除法這樣的操作來說,就非常難實現了。
使用C內置的float類型來建模一個FIR濾波器
算法可進行數字求精,以便使用定點算術來降低最終硬件或軟件實現的復雜性。在硬件方面,將整數或定點算術限制為最小位寬,可在本質上滿足性能、空間、能耗的需要;假如實現中用到了DSP處理器,那麼把算法限制為整數或定點算術,就可為特定程序使用盡可能便宜的處理器。
定點算術的建模可通過C語言內置的浮點或整數類型來完成,這做的話,需要顯式編碼並受限於C中浮點數及整數可表示的最大數:64位整數或53位尾數;這些都會給操作數的位寬帶來更多的限制,例如,2個33位的數相乘,會超過64位C整數可表示的范圍。圖2演示了一個FIR濾波器的例子,但temp變量限制為15位的定點精度,其中10位用於整數位。在這個實現中,LSB的右部位被捨棄(量化模型的截斷),而MSB的左部位也被捨棄(包裝的溢出模型),應該意識到,使用float(或double)的模型在精度上是受限的,且不能再次合成(synthesis)。同樣,由於有取整模型的嚴格位精度定義有先,又由於內置浮點類型的取整將會先被應用,所以對除法這樣的操作來說,就非常難實現了。
 使用float建模定點行為
當許多算法都能依靠本地C數據類型的精度來編寫時,對支持任意長度的整數及定點算法,大家就會抱有極大的期望,而硬件描述語言(HDL)如VHDL,走的也是同一條路。隨著C/C++越來越多地被用於高級合成與驗證工具(High-Level Synthesis and Verification tools),也證實了這種語言本質上有一個足以滿足當前及未來程序需要的數據類型庫。任意長度類型的支持,也可使數據類型的行為有一個統一的定義,而統一的語義則避免了人工實現上的一些限制。
算法C數據類型
算法C數據類型是一種基於類的C++庫,其實現了任意長度的整數及定點類型,而這些可自由訪問的類型有一系列好處,包括統一及良好定義的語義,還有媲美C/C++內置數據類型的運行時速度,對比SystemC中相應的類型,其運行速度也超過10倍以上。這些數據類型能用於任何符合C++或SystemC規范標准的程序中,並擁有高度可合成的語義。
語義
語義的統一性與一致性是避免在算法中,發生功能性錯誤的要害,以下的例子,也說明了這點:
使用float建模定點行為
當許多算法都能依靠本地C數據類型的精度來編寫時,對支持任意長度的整數及定點算法,大家就會抱有極大的期望,而硬件描述語言(HDL)如VHDL,走的也是同一條路。隨著C/C++越來越多地被用於高級合成與驗證工具(High-Level Synthesis and Verification tools),也證實了這種語言本質上有一個足以滿足當前及未來程序需要的數據類型庫。任意長度類型的支持,也可使數據類型的行為有一個統一的定義,而統一的語義則避免了人工實現上的一些限制。
算法C數據類型
算法C數據類型是一種基於類的C++庫,其實現了任意長度的整數及定點類型,而這些可自由訪問的類型有一系列好處,包括統一及良好定義的語義,還有媲美C/C++內置數據類型的運行時速度,對比SystemC中相應的類型,其運行速度也超過10倍以上。這些數據類型能用於任何符合C++或SystemC規范標准的程序中,並擁有高度可合成的語義。
語義
語義的統一性與一致性是避免在算法中,發生功能性錯誤的要害,以下的例子,也說明了這點:
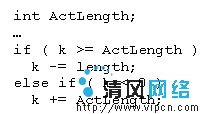 眾所周知,變量ActLength的范圍為1至255,萬一編譯器的合成不知道其范圍,就不能進行相應的優化,它的聲明就會從int變為更嚴格的sc_uint<8>類型;雖然合成會得到更好的結果,但設計就仿真得不正確了。在經過一番調試之後,找到了問題的源頭:在比較表達式k >= ActLength中,兩個操作數變成了一個signed int與一個unsigned long long(為64位無符號整數,其是sc_uint類型的基類型)之間的比較。對此的解釋是:C/C++整數提升規則指定了在進行比較之前,會把操作數int提升為一個unsigned long long,例如,假如k的值為 -1,在提升為unsigned long long之後,它會變成2^64 – 1。
像這樣語義中的問題一般會非常難以察覺,且是與位寬相關的,例如,可能有人想擴大某個現有算法的位寬,只有看到結果時,才知道是行不通的;這個問題也可能是與特定平台相關的,例如,對1 << 32(兩個操作數都是int類型,結果也是int類型)大家期望返回0,但在大多數平台(或編譯器)上,它都會返回1(沒有移位,只因為第二個操作數較低的五位被計算進來了);當第一個操作數是一個64位整數時,平台依靠性會表現得更加明顯及頻繁。主要的問題是C/C++標准沒有指定在32位整數情況下移位值(第二個操作數)超出0至31范圍、或在64位整數情況下移位值超出0至63范圍時的行為。不幸的是,像sc_int、sc_uint這樣的數據類型也不能為用戶避免這類平台依靠性的問題。
算法C數據類型被設計用於提供統一且一致的語義,因此,它們是可猜測的,例如,對有符號數混用一個無符號操作數仍會產生期望的結果;這些類型的長度不受限制,所以就不存在所謂的精度問題。所有的操作——包括移位和除法——都有完整且一致性的定義,混合不同的類型也能得到期望的結果,如,當x為一個C內置類型,而y是一個算法C類型時,表達式x+y和y+x均能返回相同的結果。
運行時間
我們的目的是為了在支持任意長度類型及避免用戶碰到前述語義問題的前提下,得到使用內置類型(位寬不超過64位)手工C/C++編碼優化過的運行時間。算法C類型是為快速執行及易於合成的語義而設計及實現的,所有操作的位寬由C++編譯器靜態確定,這就避免了動態內存分配,減少了運行時間,也使得語義更加易於合成。另外,實現也為速度進行了優化,因此可能會調用更多的專用及高效代碼,充分利用了當今編譯器的優化特性。
眾所周知,變量ActLength的范圍為1至255,萬一編譯器的合成不知道其范圍,就不能進行相應的優化,它的聲明就會從int變為更嚴格的sc_uint<8>類型;雖然合成會得到更好的結果,但設計就仿真得不正確了。在經過一番調試之後,找到了問題的源頭:在比較表達式k >= ActLength中,兩個操作數變成了一個signed int與一個unsigned long long(為64位無符號整數,其是sc_uint類型的基類型)之間的比較。對此的解釋是:C/C++整數提升規則指定了在進行比較之前,會把操作數int提升為一個unsigned long long,例如,假如k的值為 -1,在提升為unsigned long long之後,它會變成2^64 – 1。
像這樣語義中的問題一般會非常難以察覺,且是與位寬相關的,例如,可能有人想擴大某個現有算法的位寬,只有看到結果時,才知道是行不通的;這個問題也可能是與特定平台相關的,例如,對1 << 32(兩個操作數都是int類型,結果也是int類型)大家期望返回0,但在大多數平台(或編譯器)上,它都會返回1(沒有移位,只因為第二個操作數較低的五位被計算進來了);當第一個操作數是一個64位整數時,平台依靠性會表現得更加明顯及頻繁。主要的問題是C/C++標准沒有指定在32位整數情況下移位值(第二個操作數)超出0至31范圍、或在64位整數情況下移位值超出0至63范圍時的行為。不幸的是,像sc_int、sc_uint這樣的數據類型也不能為用戶避免這類平台依靠性的問題。
算法C數據類型被設計用於提供統一且一致的語義,因此,它們是可猜測的,例如,對有符號數混用一個無符號操作數仍會產生期望的結果;這些類型的長度不受限制,所以就不存在所謂的精度問題。所有的操作——包括移位和除法——都有完整且一致性的定義,混合不同的類型也能得到期望的結果,如,當x為一個C內置類型,而y是一個算法C類型時,表達式x+y和y+x均能返回相同的結果。
運行時間
我們的目的是為了在支持任意長度類型及避免用戶碰到前述語義問題的前提下,得到使用內置類型(位寬不超過64位)手工C/C++編碼優化過的運行時間。算法C類型是為快速執行及易於合成的語義而設計及實現的,所有操作的位寬由C++編譯器靜態確定,這就避免了動態內存分配,減少了運行時間,也使得語義更加易於合成。另外,實現也為速度進行了優化,因此可能會調用更多的專用及高效代碼,充分利用了當今編譯器的優化特性。
 表1:規格化為ac_fixed的運行時間比較
表1是當定點算術用算法C定點類型ac_fixed來建模時,各種不同的運行時比較;float的實現在圖2中,sc_fixed_fast為SystemC中精度受限的定點數據類型,sc_fixed為任意精度的定點類型。實際中對FIR濾波器進行10^8次調用,TRN/WRAP的運行時間為6.5秒,RND/SAT為29秒。其他類型的運行時間也能從這張表中依次推出,如sc_fixed TRN/WRAP將花費6.5s × 227 = 1476s(將近25分鐘)。作為參考,圖1中的算法(使用無定點建模的float)花費時間為3.5s(比起使用定點建模的ac_fixed,慢了近兩倍)。
上述的運行時間數據,均由GCC 4.1.1測量得來,而在之前版本的GCC或Visual C++ 2005中得到的數據大致接近。
另外,運行時間也能通過整型數據類型或位操作進一步縮短。表2為一個DCT算法的相應結果,它由一個每次讀寫2位的移位操作得來,與此對比的運行時間為SystemC精度受限的sc_int與任意長度的sc_bigint。
表1:規格化為ac_fixed的運行時間比較
表1是當定點算術用算法C定點類型ac_fixed來建模時,各種不同的運行時比較;float的實現在圖2中,sc_fixed_fast為SystemC中精度受限的定點數據類型,sc_fixed為任意精度的定點類型。實際中對FIR濾波器進行10^8次調用,TRN/WRAP的運行時間為6.5秒,RND/SAT為29秒。其他類型的運行時間也能從這張表中依次推出,如sc_fixed TRN/WRAP將花費6.5s × 227 = 1476s(將近25分鐘)。作為參考,圖1中的算法(使用無定點建模的float)花費時間為3.5s(比起使用定點建模的ac_fixed,慢了近兩倍)。
上述的運行時間數據,均由GCC 4.1.1測量得來,而在之前版本的GCC或Visual C++ 2005中得到的數據大致接近。
另外,運行時間也能通過整型數據類型或位操作進一步縮短。表2為一個DCT算法的相應結果,它由一個每次讀寫2位的移位操作得來,與此對比的運行時間為SystemC精度受限的sc_int與任意長度的sc_bigint。
 表2:規格化為ac_int的運行時間比較
結論
基於通用標准ANSI C++,這種新的整數與定點算法C類型答應算法及系統設計者指定任意位寬,從而提供比傳統數據類型高200倍的仿真效率。這些新數據類型可成為C-to-RTL設計鏈中非常有價值的一環,及在整個實現流程中保證了任意位寬的精度。
表2:規格化為ac_int的運行時間比較
結論
基於通用標准ANSI C++,這種新的整數與定點算法C類型答應算法及系統設計者指定任意位寬,從而提供比傳統數據類型高200倍的仿真效率。這些新數據類型可成為C-to-RTL設計鏈中非常有價值的一環,及在整個實現流程中保證了任意位寬的精度。