一、前言
用計算機進行數字圖像處理的目的有兩個,一是產生更適合人類視覺觀察和識別的圖像,二是希望計算機能夠自動進行識別和理解圖像。無論是為了何種目的,圖像處理的要害一步是對包含有大量各式各樣景物信息的圖像進行分解。分解的最終結果就是圖像被分成一些具有各種特征的最小成分,這些成分就稱為圖像的基元。產生這些基元的過程就是圖像分割的過程。圖像分割作為圖像處理領域中極為重要的內容之一,是實現圖像分析與理解的基礎。從概念上來說,所謂圖像分割就是按照一定的原則將一幅圖像或景物分為若干個部分或子集的過程。目前圖像處理系統中我們只能得到二維圖像信息,因此只能進行圖像分割而不是景物分割(景物是三維信息);圖像分割也可以理解為將圖像中有意義的特征區域或者需要應用的特征區域提取出來,這些特征區域可以是像素的灰度值、物體輪廓曲線、紋理特性等,也可以是空間頻譜或直方圖特征等。在圖像中用來表示某一物體的區域,其特征都是相近或相同的,但是不同物體的區域之間,特征就會急劇變化。目前已經提出的圖像分割方法很多,從分割依據的角度來看,圖像的分割方法可以分為相似性分割和非連續性分割。相似性分割就是將具有同一灰度級或相同組織結構的像素聚集在一起,形成圖像的不同區域;非連續性分割就是首先檢測局部不連續性,然後將它們連接在一起形成邊界,這些邊界將圖像分成不同的區域。由於不同種類的圖像,不同的應用場合,需要提取的圖像特征是不同的,當然對應的圖像特征提取方法也就不同,因此並不存在一種普遍適應的最優方法。
圖像分割方法又可分為結構分割方法和非結構分割方法兩大類。結構分割方法是根據圖像的局部區域象素的特征來實現圖像分割,如阈值分割、區域生長、邊緣檢測、紋理分析等,這些方法假定事先知道這些區域的特性,或者在處理過程中能夠求得這些特性,從而能夠尋找各種形態或研究各像素群。非結構分割法包括統計模式識別、神經網絡方法或其它利用景物的先驗知識實現的方法等等。這些內容由於專業性很強,就不在本文討論內容中了,有愛好的讀者可以參考圖像處理的專業書籍。總之,圖像分割可以分為圖像的邊緣提取和圖像的二值化二部分內容,下面我們首先來討論一下各種常用的圖像邊緣提取的方法。
二、圖像邊緣檢測
數字圖像的邊緣檢測是圖像分割、目標區域的識別、區域外形提取等圖像分析領域十分重要的基礎,是圖像識別中提取圖像特征的一個重要屬性,圖像理解和分析的第一步往往就是邊緣檢測,目前它以成為機器視覺研究領域最活躍的課題之一,在工程應用中占有十分重要的地位。物體的邊緣是以圖像的局部特征不連續的形式出現的,也就是指圖像局部亮度變化最顯著的部分,例如灰度值的突變、顏色的突變、紋理結構的突變等,同時物體的邊緣也是不同區域的分界處。圖像邊緣有方向和幅度兩個特性,通常沿邊緣的走向灰度變化平緩,垂直於邊緣走向的像素灰度變換劇烈,根據灰度變化的特點,可分為階躍型、房頂型和凸緣型,如圖一所示,這些變化對應圖像中不同的景物。需要讀者注重的是,實際分析中圖像要復雜的多,圖像邊緣的灰度變化情況並不僅限於上述標准情況。

(a)階躍型

(b) 房頂型

(c) 凸緣型
圖一 邊緣灰度變換的幾種類型
由於邊緣是圖像上灰度變化最劇烈的地方,傳統的邊緣檢測就是利用了這個特點,對圖像各個像素點進行微分或求二階微分來確定邊緣像素點。一階微分圖像的峰值處對應著圖像的邊緣點;二階微分圖像的過零點處對應著圖像的邊緣點。根據數字圖像的特點,處理圖像過程中常采用差分來代替導數運算,對於圖像的簡單一階導數運算,由於具有固定的方向性,只能檢測特定方向的邊緣,所以不具有普遍性。為了克服一階導數的缺點,我們定義了圖像的梯度為梯度算子為

,它是圖像處理中最常用的一階微分算法,式子中
表示圖像的灰度值,圖像梯度的最重要性質是梯度的方向是在圖像灰度最大變化率上,它恰好可以放映出圖像邊緣上的灰度變化。
圖像邊緣提取的常用梯度算子有Robert算子、Sobel算子、Prewitt算子、Krisch算子等。下面以邊緣檢測Sobel算子為例來講述數字圖像處理中邊緣檢測的實現:
對於數字圖像,可以用一階差分代替一階微分;
△xf(x,y)=f(x,y)-f(x-1,y);
△yf(x,y)=f(x,y)-f(x,y-1);
求梯度時對於平方和運算及開方運算,可以用兩個分量的絕對值之和表示,即:
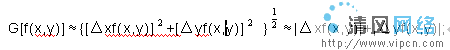
Sobel梯度算子是先做成加權平均,再微分,然後求梯度,即:
△xf(x,y)= f(x-1,y+1) + 2f(x,y+1) + f(x+1,y+1)- f(x-1,y-1) - 2f(x,y-1) - f(x+1,y-1);
△yf(x,y)= f(x-1,y-1) + 2f(x-1,y) + f(x-1,y+1)- f(x+1,y-1) - 2f(x+1,y) - f(x+1,y+1);
G[f(x,y)]=△xf(x,y)+△yf(x,y);
上述各式中的像素之間的關系見圖二
F(x-1,y-1) F(x,y-1) F(x+1,y-1) F(x-1,y) F(x,y) F(x+1,y) F(x-1,y+1) F(x,y+1) F(x+1,y+1) 圖二 Sober算子中各個像素點的關系圖
我在視圖類中定義了響應菜單命令的邊緣檢測Sobel算子實現灰度圖像邊緣檢測的函數(圖像數據的獲取可以參見我在天極網上發表的的相關文章):
void CDibView::OnMENUSobel()
{
CClientDC pDC(this);
HDC hDC=pDC.GetSafeHdc();//獲取當前設備上下文的句柄;
SetStretchBltMode(hDC,COLORONCOLOR);
HANDLE data1handle;
LPDIBHDRTMAPINFOHEADER lpDIBHdr;
CDibDoc *pDoc=GetDocument();
HDIB hdib;
unsigned char *lpDIBBits;
unsigned char *data;
hdib=pDoc->m_hDIB;//得到圖象數據;
lpDIBHdr=(LPDIBHDRTMAPINFOHEADER)GlobalLock((HGLOBAL)hdib);
lpDIBBits= lpDIBHdr +* (LPDWord)lpDIBHdr + 256*sizeof(RGBQUAD);
//得到指向位圖像素值的指針;
data1handle=GlobalAlloc(GMEM_SHARE,WIDTHBYTES(lpDIBHdr->biWidth*8)*lpDIBHdr->biHeight); //申請存放處理後的像素值的緩沖區
data=(unsigned char*)GlobalLock((HGLOBAL)data1handle);
AfxGetApp()->BeginWaitCursor();
int i,j,buf,buf1,buf2;
for( j=0; jbiHeight; j++)//以下循環求(x,y)位置的灰度值
for( i=0; ibiWidth; i++)
{
if(((i-1)>=0)&&((i+1)biWidth)&&((j-1)>=0)&&((j+1)biHeight))
{//對於圖像四面邊界處的向素點不處理
buf1=(int)*(lpDIBBits+(i+1)*WIDTHBYTES(lpDIBHdr->biWidth*8)+(j-1))
+2*(int)*(lpDIBBits+(i+1)*WIDTHBYTES(lpDIBHdr->biWidth*8)+(j))
+(int)(int)*(lpDIBBits+(i+1)*WIDTHBYTES(lpDIBHdr->biWidth*8)+(j+1));
buf1=buf1-(int)(int)*(lpDIBBits+(i-1)*WIDTHBYTES(lpDIBHdr->biWidth*8)+(j-1))
-2*(int)(int)*(lpDIBBits+(i-1)*WIDTHBYTES(lpDIBHdr->biWidth*8)+(j))
-(int)(int)*(lpDIBBits+(i-1)*WIDTHBYTES(lpDIBHdr->biWidth*8)+(j+1));
//以上是對圖像進行水平(x)方向的加權微分
buf2=(int)(int)*(lpDIBBits+(i-1)*WIDTHBYTES(lpDIBHdr->biWidth*8)+(j+1))
+2*(int)(int)*(lpDIBBits+(i)*WIDTHBYTES(lpDIBHdr->biWidth*8)+(j+1))
+(int)(int)*(lpDIBBits+(i+1)*WIDTHBYTES(lpDIBHdr->biWidth*8)+(j+1));
buf2=buf2-(int)(int)*(lpDIBBits+(i-1)*WIDTHBYTES(lpDIBHdr->biWidth*8)+(j-1))
-2*(int)(int)*(lpDIBBits+(i)*WIDTHBYTES(lpDIBHdr->biWidth*8)+(j-1))
-(int)(int)*(lpDIBBits+(i+1)*WIDTHBYTES(lpDIBHdr->biWidth*8)+(j-1));
//以上是對圖像進行垂直(y)方向加權微分
buf=abs(buf1)+abs(buf2);//求梯度
if(buf>255) buf=255;
if(buf<0)buf=0;
*(data+i*WIDTHBYTES(lpDIBHdr->biWidth*8)+j)=(BYTE)buf;
}
else *(data+i*lpDIBHdr->biWidth+j)=(BYTE)0;
}
for( j=0; jbiHeight; j++)
for( i=0; ibiWidth; i++)
*(lpDIBBits+i*WIDTHBYTES(lpDIBHdr->biWidth*8)+j)=*(data+i*WIDTHBYTES(lpDIBHdr->biWidth*8)+j); //處理後的數據寫回原緩沖區
StretchDIBits (hDC,0,0,lpDIBHdr->biWidth,lpDIBHdr->biHeight,0,0,
lpDIBHdr->biWidth,lpDIBHdr->biHeight,
lpDIBBits,(LPDIBHDRTMAPINFO)lpDIBHdr,
DIB_RGB_COLORS,
SRCCOPY);
}
上述的數學分析讀者可能看起來有些吃力,不過不要緊,對與邊緣檢測,大家只要知道有若干個檢測模板(既邊緣檢測矩陣)可以直接實現檢測功能就行了,現在將常用的檢測實現公式列出如下(檢測模版可以從相應的算法很輕易的得到):
Roberts算子:G[i,i]=f[i,j]-f[i+1,j+1]+f[i+1,j]-f[i,j+1];
Sobe算子:G[i,i]=f[i-1,j+1]+2f[i,j+1]+f[i+1,j+1]-f[i-1,j-1]-2f[i,j-1]-f[i+1,j-1]
+f[i-1,j-1]+2f[i-1,j]+f[i-1,j+1]-f[i+1,j-1]-2f[i+1,j]-f[i+1,j+1];
其中G[i,j]表示處理後(i,j)點的灰度值,f[i,j]表示處理前該點的灰度值。Photoshop教程 數據結構 五筆輸入法專題 QQ病毒專題 共享上網專題 Google工具和服務專題
Kirsch算子實現起來相對來說稍微麻煩一些,它采用8個模板對圖像上的每一個像素點進行卷積求導數,這8個模板代表8個方向,對圖像上的8個特定邊緣方向作出最大響應,運算中取最大值作為圖像的邊緣輸出(上述算法中用到的8個模板在下面的實現代碼中給出)。為了便於讀者理解該算法的實現,這裡我們給出實現該算法的函數代碼,讀者可以稍加改動應用到自己的項目中去。
BOOL Kirsch(BYTE *pData,int Width,int Height)
{//定義實現Kirsch算法的8個模板;
int i,j,s,t,k,max,sum[8];
static a[3][3]={{+5,+5,+5},{-3,0,-3},{-3,-3,-3}};
static a1[3][3]={{-3,+5,+5},{-3,0,+5},{-3,-3,-3}};
static a2[3][3]={{-3,-3,+5},{-3,0,+5},{-3,-3,+5}};
static a3[3][3]={{-3,-3,-3},{-3,0,+5},{-3,+5,+5}};
static a4[3][3]={{-3,-3,-3},{-3,0,-3},{+5,+5,+5}};
static a5[3][3]={{-3,-3,-3},{+5,0,-3},{+5,+5,-3}};
static a6[3][3]={{+5,-3,-3},{+5,0,-3},{+5,-3,-3}};
static a7[3][3]={{+5,+5,-3},{+5,0,-3},{-3,-3,-3}};
BYTE *pData1;
if(pData==NULL)
{
AfxMessageBox("圖像數據為空,請讀取圖像數據!");
return FALSE;
}
pData1=(BYTE*)new char[Width*Height];
if(pData1==NULL)
{
AfxMessageBox("圖像緩沖數據區申請失敗,請重新申請圖像數據緩沖區!");
return FALSE ;
}
memcpy(pData1,pData, Width*8*Height);
//kirsch算子處理,對每一像素點求取八個方向的導數;;
for(i=1;i<Height-1;i++)
for(j=1;j<Width-1;j++)
{
sum[1]=sum[2]=sum[3]=sum[4]=sum[5]=sum[6]=sum[7]=sum[8]=0;
for(t=-1;t<2;t++)
{
for(s=-1;s<2;s++)
{ sum[1]+=*(pData+WIDTHBYTES(Width*8)*(i+t)+j+s)*a[1+t][1+s];
sum[2]+=*(pData+WIDTHBYTES(Width*8)*(i+t)+j+s)*a1[1+t][1+s]; sum[3]+=*(pData+WIDTHBYTES(Width*8)*(i+t)+j+s)*a2[1+t][1+s]; sum[4]+=*(pData+WIDTHBYTES(Width*8)*(i+t)+j+s)*a3[1+t][1+s]; sum[5]+=*(pData+WIDTHBYTES(Width*8)*(i+t)+j+s)*a4[1+t][1+s]; sum[6]+=*(pData+WIDTHBYTES(Width*8)*(i+t)+j+s)*a5[1+t][1+s]; sum[7]+=*(pData+WIDTHBYTES(Width*8)*(i+t)+j+s)*a6[1+t][1+s]; sum[8]+=*(pData+WIDTHBYTES(Width*8)*(i+t)+j+s)*a7[1+t][1+s];
}
}
//取最大方向的導數;
for(k=0;k<8;k++)
{
max=0;
if(max<sum[k])
max=sum[k];
}
if(max<0)
max=0;
if(max>255)
max=255;
*(pData1+ Width*8*i+j)=max;
}
memcpy(pData,pData1, Width*8*Height);
delete pData1;
return TRUE;
}
另外還有一種稱為拉普拉斯的算子是不依靠於邊緣方向的二階微分算子,其表示式

,對於數字圖像來說拉普拉斯算子可以簡單表示為:G[I,j]=f[i+1,j]+f[i-1,j]+f(i,j+1)+f[i,j-1]-4f[i,j];它是一個標量而不是向量,具有旋轉不變,既各向同性的性質,它經常用在圖像處理的過程中。
梯度算子和拉普拉斯算子對噪聲敏感,它們都使噪聲成份加強,因此在處理含有較大噪聲的圖像時,經常先對圖像進行平滑操作,然後再進行二階微分,這就產生了所謂的LOG(又稱為Marr方法)邊緣檢測方法。它先用高斯函數對圖像進行平滑,然後再用拉普拉斯算子進行運算。
總的來說,傳統的邊緣檢測算子的噪聲平滑能力和邊緣定位能力是矛盾的,為了克服這個不足,正確地得到圖像的邊緣信息,人們提出了很多方法,如多尺度空間濾波、Facet模型檢測邊緣、模板匹配、Hough變換、小波變換、人工神經網絡、模糊推理等算法。但這些方法絕大多數沒有經典的算法精簡,要麼難以獲得合理的計算復雜度,要麼需要人為的調節各種參數,有時甚至難以實時運行。因為傳統邊緣的定義為圖像中灰度的突變,所以這樣定義邊緣既失去了邊緣的部分信息,又把噪聲的影響包含在了邊緣中。其實,邊緣往往具有以下特征:
1)灰度突變;
2)是不同區域的邊界;
3)具有方向性;
根據邊緣的這三個特征,可以判定所關心的區域其特征是否存在差異來判定是否存在邊緣的可能性。假如特征沒有差異,則認為是平滑區;假如特征有差異,則判定為邊緣點。算法的具體實現步驟如下:
1) 設置四個3x3模板如圖三所示,顯而易見,四個模板分別按0、45、90、135以(x,y)點為中心將3x3的區域分成兩個部分,按照這四個模板分別對圖像中的每一像素點進行卷積求和操作。
2)對圖像中每一像素點求的四個結果求絕對值,將每個結果分別與一個阈值比較,假如其中任意一結果大於或等於阈值T,則該模板的中心點所對應的圖像像素點的灰度值為255,否則為0。
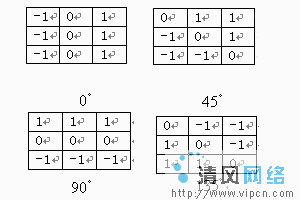
圖三 邊緣提取模板
對於有噪聲的圖像,由於噪聲是隨機分布的,因此不論(x,y)是有效邊界點還是處於平坦區域內部,沿邊緣方向劃分的兩個區域R1和R2的噪聲分布和噪聲強度,在概率上相同。從四個模板的結構可以看出,噪聲的影響基本上被相應的抵消,不會對邊緣提取產生太大的影響,因此該算法具有較好的抗噪能力,克服了傳統的邊界提取僅考慮灰度突變的情況的局限。經實驗證實該方法有較強的抗噪聲性能。為了更好的對比各種算法進行邊緣檢測的效果,我們對一幅汽車圖像進行了處理,下圖中的a、b、c、d是分別通過LOG算子、Sober算子、Kirsch算子和使用上述算法檢測得到的邊緣。

(a) 原始圖像

(b)LOG算子

(c) Sober算子

(d) Kirsch算子

(e) 模板檢測法
圖四 圖像的邊緣檢測
從上面的處理後的效果圖來說,只有最後一種算法處理後肉眼看不出有噪聲點,所以從去噪和提取邊緣的綜合效果來看,我們上述介紹的模板檢測算法還是比較另人滿足的。Photoshop教程 數據結構 五筆輸入法專題 QQ病毒專題 共享上網專題 Google工具和服務專題
三、圖像的二值化
所謂二值圖像,就是指圖像上的所有點的灰度值只用兩種可能,不為"0"就為"255",也就是整個圖像呈現出明顯的黑白效果。為了得到理想的二值圖像,一般采用阈值分割技術,它對物體與背景有較強對比的圖像的分割非凡有效,它計算簡單而且總能用封閉、連通的邊界定義不交疊的區域。所有灰度大於或等於阈值的像素被判決為屬於物體,灰度值用"255"表示,否則這些像素點被排除在物體區域以外,灰度值為"0",表示背景。這樣一來物體的邊界就成為這樣一些內部的點的集合,這些點都至少有一個鄰點不屬於該物體。假如感愛好的物體在內部有均勻一致的灰度值,並且其處在一個具有另外一個灰度值的均勻背景下,使用阈值法可以得到比較好的效果。假如物體同背景的差別不在灰度值上(比如紋理不同),可以將這個性質轉換為灰度的差別,然後利用阈值化技術來分割該圖像。為了使分割更加魯棒,適用性更強,系統應該可以自動選擇阈值。基於物體、環境和應用域等知識的圖像分割算法比基於固定阈值的算法更具有普遍性和適應性。這些知識包括:對應於物體的圖像灰度特性、物體的尺寸、物體在圖像中所占的比例、圖像中不同類型物體的數量等。其中圖像直方圖就是一種灰度特性,通常被用來作為分割圖像的工具。
阈值分割法分為全局阈值法和局部阈值分割法。所謂局部阈值分割法是將原始圖像劃分成較小的圖像,並對每個子圖像選取相應的阈值。在阈值分割後,相鄰子圖像之間的邊界處可能產生灰度級的不連續性,因此需用平滑技術進行排除。局部阈值法常用的方法有灰度差直方圖法、微分直方圖法。局部阈值分割法雖然能改善分割效果,但存在幾個缺點:
(1)每幅子圖像的尺寸不能太小,否則統計出的結果無意義。
(2)每幅圖像的分割是任意的,假如有一幅子圖像正好落在目標區域或背景區域,而根據統計結果對其進行分割,也許會產生更差的結果。
(3)局部阈值法對每一幅子圖像都要進行統計,速度慢,難以適應實時性的要求。
全局阈值分割方法在圖像處理中應用比較多,它在整幅圖像內采用固定的阈值分割圖像。經典的阈值選取以灰度直方圖為處理對象。根據阈值選擇方法的不同,可以分為模態方法、迭代式阈值選擇等方法。這些方法都是以圖像的直方圖為研究對象來確定分割的阈值的。另外還有類間方差阈值分割法、二維最大熵分割法、模糊阈值分割法、共生矩陣分割法、區域生長法等等。
對於比較簡單的圖像,可以假定物體和背景分別處於不同的灰度級,圖像被零均值高斯噪聲污染,所以圖像的灰度分布曲線近似認為是由兩個正態分布函數(
)和(

)疊加而成,圖像的直方圖將會出現兩個分離的峰值,如圖五所示。對於這樣的圖像,分割阈值可以選擇直方圖的兩個波峰間的波谷所對應的灰度值作為分割的阈值。這種分割方法不可避免的會出現誤分割,使一部分本屬於背景的像素被判決為物體,屬於物體的一部分像素同樣會被誤認為是背景。可以證實,當物體的尺寸和背景相等時,這樣選擇阈值可以使誤分概率達到最小。在大多數情況下,由於圖像的直方圖在波谷四周的像素很稀疏,因此這種方法對圖像的分割影響不大。這一方法可以推廣到具有不同灰度均值的多物體圖像。
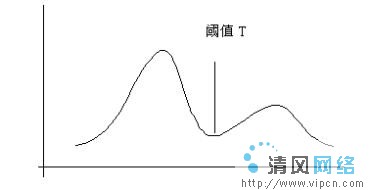
圖五 雙峰直方圖
迭代式阈值選擇算法是對上一種方法的改進,它首先選擇一個近似阈值T,將圖像分割成兩部分
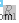
和

,計算區域
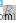
和

的均值
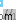
和

,選擇新的分割阈值T=(

)/2,重復上述步驟直到
和

不再變化為止。Photoshop教程 數據結構 五筆輸入法專題 QQ病毒專題 共享上網專題 Google工具和服務專題
後來"熵"的概念被引入了圖像處理技術,人們提出了許多基於熵的阈值分割法。1980年,Pun提出了最大後驗熵上限法,1985年,Kapur等人提出了一維最大熵阈值法,1989年Arutaleb將一維最大熵阈值法與Kirby等人的二維阈值方法相結合,提出了二維熵阈值法。對於一維最大熵分割方法,它的思想是統計圖像中每一個灰度級出現的概率
,計算該灰度級的熵
,假設以灰度級T分割圖像,圖像中低於T灰度級的像素點構成目標物體(O),高於灰度級T的像素點構成背景(B),那麼各個灰度級在本區的分布概率為:
O區:
i=1,2……,t
B區:

i=t+1,t+2……L-1
上式中的

,這樣對於數字圖像中的目標和背景區域的熵分別為:
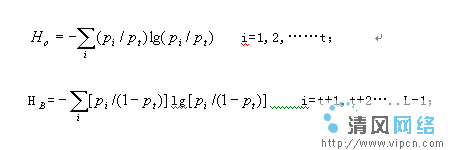
對圖像中的每一個灰度級分別求取w=
,選取使w最大的灰度級作為分割圖像的阈值,這就是一維最大熵阈值圖像分割法。我們定義了一個函數GetMaxHtoThrod()來實現該算法,它的返回值就是用來分割圖像的阈值。
int GetMaxHtoThrod(BYTE *pData,int Width,int Height)
{
int i,j,t;
float p[256],a1,a2,num[256],max,pt;
if(pData==NULL)
{
AfxMessageBox("圖像數據為空,請讀取圖像數據!");
return -1;
}
//初始化數組p[];
for(i=0;i<256;i++)
p[i]=0.0f;
//統計各個灰度級出現的次數;
for(i=0;i<Height;i++)
for(j=0;j<Width;j++)
{
p[*(pData+ Width*8)*i+j]++;
}
//統計各個灰度級出現的概率;
for(j=0;j<256;j++)
{
p[j]=p[j]/(Width*Height);
}
//對每一個灰度級進行比較;
for(i=0;i<256;i++)
{
a1=a2=0.0f;
pt=0.0f;
for(j=0;j<=i;j++)
{
pt+=p[j];
}
for(j=0;j<=i;j++)
{
a1+=(float)p[j]/pt*logf(p[j]/pt);
}
for(j=i+1;j<256;j++)
{
a2+=(float)p[j]/(1-pt)*logf(p[j]/(1-pt));
}
num[i]=a1+a2;
}
max=0.0f;
//找到使類的熵最大的灰度級;
for(i=0;i<256;i++)
{
if(max<num[i])
{
max=num[i];
t=i;
}
}
return t;
}
這種方法的缺點是僅僅考慮了像素點的灰度信息,沒有考慮到像素點的空間信息,所以當圖像的信噪比降低時分割效果不理想。毫無疑問,像素點的灰度是最基本的特征,但它對噪聲比較敏感,為此,在分割圖像時可以再考慮圖像的區域信息,區域灰度特征包含了圖像的部分空間信息,且對噪聲的敏感程度要低於點灰度特征。綜合利用圖像的這兩個特征就產生了二維最大熵阈值分割方法。二維最大熵阈值分割算法實現時首先以原始灰度圖像中各個像素的每一個像素及其四鄰域的四個像素構成一個區域,該像素點的灰度值i和四鄰域的均值j構成一個二維向量(i,j),統計(i,j)的發生概率

,假如圖像的最大灰度級為

,那麼

(i,j=0,1…

)就構成了該圖像關於點灰度-區域均值的二維直方圖。對於給定的圖像,由於大部份的像素點屬於目標區域或背景,而目標和背景區域內部像素點的灰度級比較均勻,像素點的灰度和其鄰域均值的灰度級相差不大,所以圖像對應的二維直方圖

主要集中在i,j平面的對角線四周,並且在總體上呈現雙峰和一谷的狀態,兩個峰分別對應於目標和背景。在遠離IOJ平面對角線的坐標處,峰的高度迅速下降,這部分對應著圖像中的噪聲點、雜散點和邊緣點。二維直方圖的IOJ平面圖如圖六所示,沿對角線的方向分布的A區、B區分別代表目標和背景,遠離對角線分布的C區、D區分別代表邊界和噪聲,所以應該在A區和B區上用點灰度-區域灰度平均值二維最大熵法確定阈值,使之分割的目標和背景的信息量最大。
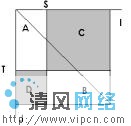
圖 六 二維直方圖的IOJ平面圖
確定二維最大熵的算法和確定一維最大熵算法類似,設分割圖像的阈值為(s,t),則A區、B區概率分別為:
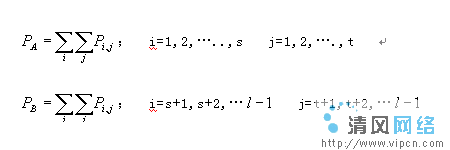
則A區、B區的二維熵分別為:
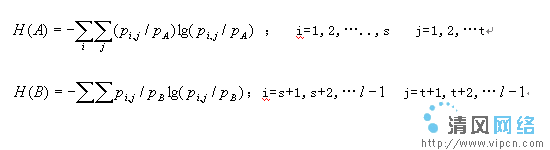
對於確定圖像的二維直方圖,對不同的(
)分別計算w=H(A)+H(B),選取使w達到最大的(

)作為最佳分割圖像的阈值。該算法實現的函數和上述一維最大熵算法大同小異,只是在二值化時對圖像上的像素點不僅要考慮灰度值,同時還要考慮該點鄰域的灰度均值。

(a)標准lena圖像

(b)一維最大熵

(c) 二維最大熵
圖七 二值圖像
上圖中a、b、c分別顯示了標准lena圖像、采用一維最大熵法、二維最大熵法得到的分割效果。可以看出,二維最大熵法可以很好的分割包含目標和背景兩類區域的圖像,效果最好。
由於篇幅有限,本文只能是蜻蜓點水一般對比較非凡的分割算法介紹了一下,其實無論二值化還是邊緣提取的處理,對應的算法都很多,都各有特色,讀者可以針對不同的圖像,結合前人提出的各種算法,找到實際應用中最佳的處理效果。



 ,它是圖像處理中最常用的一階微分算法,式子中
,它是圖像處理中最常用的一階微分算法,式子中 表示圖像的灰度值,圖像梯度的最重要性質是梯度的方向是在圖像灰度最大變化率上,它恰好可以放映出圖像邊緣上的灰度變化。
表示圖像的灰度值,圖像梯度的最重要性質是梯度的方向是在圖像灰度最大變化率上,它恰好可以放映出圖像邊緣上的灰度變化。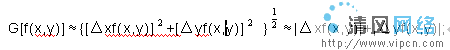
 ,對於數字圖像來說拉普拉斯算子可以簡單表示為:G[I,j]=f[i+1,j]+f[i-1,j]+f(i,j+1)+f[i,j-1]-4f[i,j];它是一個標量而不是向量,具有旋轉不變,既各向同性的性質,它經常用在圖像處理的過程中。
,對於數字圖像來說拉普拉斯算子可以簡單表示為:G[I,j]=f[i+1,j]+f[i-1,j]+f(i,j+1)+f[i,j-1]-4f[i,j];它是一個標量而不是向量,具有旋轉不變,既各向同性的性質,它經常用在圖像處理的過程中。





 )和(
)和( )疊加而成,圖像的直方圖將會出現兩個分離的峰值,如圖五所示。對於這樣的圖像,分割阈值可以選擇直方圖的兩個波峰間的波谷所對應的灰度值作為分割的阈值。這種分割方法不可避免的會出現誤分割,使一部分本屬於背景的像素被判決為物體,屬於物體的一部分像素同樣會被誤認為是背景。可以證實,當物體的尺寸和背景相等時,這樣選擇阈值可以使誤分概率達到最小。在大多數情況下,由於圖像的直方圖在波谷四周的像素很稀疏,因此這種方法對圖像的分割影響不大。這一方法可以推廣到具有不同灰度均值的多物體圖像。
)疊加而成,圖像的直方圖將會出現兩個分離的峰值,如圖五所示。對於這樣的圖像,分割阈值可以選擇直方圖的兩個波峰間的波谷所對應的灰度值作為分割的阈值。這種分割方法不可避免的會出現誤分割,使一部分本屬於背景的像素被判決為物體,屬於物體的一部分像素同樣會被誤認為是背景。可以證實,當物體的尺寸和背景相等時,這樣選擇阈值可以使誤分概率達到最小。在大多數情況下,由於圖像的直方圖在波谷四周的像素很稀疏,因此這種方法對圖像的分割影響不大。這一方法可以推廣到具有不同灰度均值的多物體圖像。
 和
和  ,計算區域
,計算區域 和
和 的均值
的均值 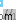 和
和 ,選擇新的分割阈值T=(
,選擇新的分割阈值T=( )/2,重復上述步驟直到
)/2,重復上述步驟直到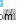 和
和 不再變化為止。Photoshop教程 數據結構 五筆輸入法專題 QQ病毒專題 共享上網專題 Google工具和服務專題
後來"熵"的概念被引入了圖像處理技術,人們提出了許多基於熵的阈值分割法。1980年,Pun提出了最大後驗熵上限法,1985年,Kapur等人提出了一維最大熵阈值法,1989年Arutaleb將一維最大熵阈值法與Kirby等人的二維阈值方法相結合,提出了二維熵阈值法。對於一維最大熵分割方法,它的思想是統計圖像中每一個灰度級出現的概率
不再變化為止。Photoshop教程 數據結構 五筆輸入法專題 QQ病毒專題 共享上網專題 Google工具和服務專題
後來"熵"的概念被引入了圖像處理技術,人們提出了許多基於熵的阈值分割法。1980年,Pun提出了最大後驗熵上限法,1985年,Kapur等人提出了一維最大熵阈值法,1989年Arutaleb將一維最大熵阈值法與Kirby等人的二維阈值方法相結合,提出了二維熵阈值法。對於一維最大熵分割方法,它的思想是統計圖像中每一個灰度級出現的概率 ,計算該灰度級的熵
,計算該灰度級的熵 ,假設以灰度級T分割圖像,圖像中低於T灰度級的像素點構成目標物體(O),高於灰度級T的像素點構成背景(B),那麼各個灰度級在本區的分布概率為:
,假設以灰度級T分割圖像,圖像中低於T灰度級的像素點構成目標物體(O),高於灰度級T的像素點構成背景(B),那麼各個灰度級在本區的分布概率為: i=1,2……,t
i=1,2……,t  i=t+1,t+2……L-1
i=t+1,t+2……L-1  ,這樣對於數字圖像中的目標和背景區域的熵分別為:
,這樣對於數字圖像中的目標和背景區域的熵分別為: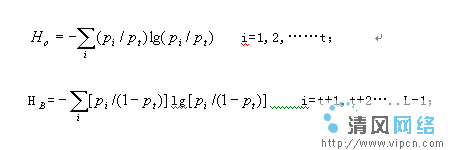
 ,選取使w最大的灰度級作為分割圖像的阈值,這就是一維最大熵阈值圖像分割法。我們定義了一個函數GetMaxHtoThrod()來實現該算法,它的返回值就是用來分割圖像的阈值。
,選取使w最大的灰度級作為分割圖像的阈值,這就是一維最大熵阈值圖像分割法。我們定義了一個函數GetMaxHtoThrod()來實現該算法,它的返回值就是用來分割圖像的阈值。 ,假如圖像的最大灰度級為
,假如圖像的最大灰度級為
 ,那麼
,那麼  (i,j=0,1…
(i,j=0,1… )就構成了該圖像關於點灰度-區域均值的二維直方圖。對於給定的圖像,由於大部份的像素點屬於目標區域或背景,而目標和背景區域內部像素點的灰度級比較均勻,像素點的灰度和其鄰域均值的灰度級相差不大,所以圖像對應的二維直方圖
)就構成了該圖像關於點灰度-區域均值的二維直方圖。對於給定的圖像,由於大部份的像素點屬於目標區域或背景,而目標和背景區域內部像素點的灰度級比較均勻,像素點的灰度和其鄰域均值的灰度級相差不大,所以圖像對應的二維直方圖 主要集中在i,j平面的對角線四周,並且在總體上呈現雙峰和一谷的狀態,兩個峰分別對應於目標和背景。在遠離IOJ平面對角線的坐標處,峰的高度迅速下降,這部分對應著圖像中的噪聲點、雜散點和邊緣點。二維直方圖的IOJ平面圖如圖六所示,沿對角線的方向分布的A區、B區分別代表目標和背景,遠離對角線分布的C區、D區分別代表邊界和噪聲,所以應該在A區和B區上用點灰度-區域灰度平均值二維最大熵法確定阈值,使之分割的目標和背景的信息量最大。
主要集中在i,j平面的對角線四周,並且在總體上呈現雙峰和一谷的狀態,兩個峰分別對應於目標和背景。在遠離IOJ平面對角線的坐標處,峰的高度迅速下降,這部分對應著圖像中的噪聲點、雜散點和邊緣點。二維直方圖的IOJ平面圖如圖六所示,沿對角線的方向分布的A區、B區分別代表目標和背景,遠離對角線分布的C區、D區分別代表邊界和噪聲,所以應該在A區和B區上用點灰度-區域灰度平均值二維最大熵法確定阈值,使之分割的目標和背景的信息量最大。
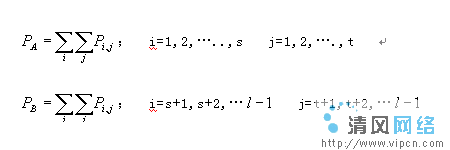
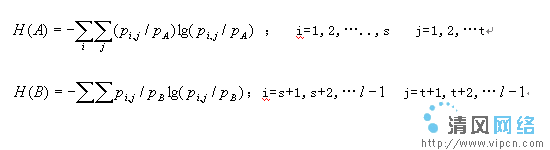
 )分別計算w=H(A)+H(B),選取使w達到最大的(
)分別計算w=H(A)+H(B),選取使w達到最大的( )作為最佳分割圖像的阈值。該算法實現的函數和上述一維最大熵算法大同小異,只是在二值化時對圖像上的像素點不僅要考慮灰度值,同時還要考慮該點鄰域的灰度均值。
)作為最佳分割圖像的阈值。該算法實現的函數和上述一維最大熵算法大同小異,只是在二值化時對圖像上的像素點不僅要考慮灰度值,同時還要考慮該點鄰域的灰度均值。

