游走 bzoj 3143，bzoj3143

游走 bzoj 3143，bzoj3143

游走（2s 128MB）walk

【問題描述】

【輸入格式】

【輸出格式】

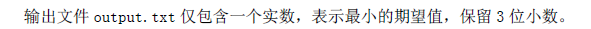
【樣例輸入】

3 3

2 3

1 2

1 3

【樣例輸出】

3.333

【樣例說明】

題解：

主要算法：貪心；高斯消元；

題意是給一個簡單無向連通圖，給每條邊賦上權值，使期望值最小

貪心讓被走到概率大的邊的權值小，就可得到最小的期望值

設每個點被走到的概率為p, 出度為d

那麼p[i] = Σ p[j] / d[j] (i，j 之間有連邊) (從 j 出發選到 i 與 j 連邊的概率為 1 / d[j])

移項得 Σ p[j] / d[j] - p[i] = 0

對於每個點我們都可以列出一個含有n個未知數的方程

特別地，p[1]概率需要加一 , p[n] = 1 (起點為1，終點為n)

那麼就可以進行高斯消元啦

 1 #include<algorithm>
 2 #include<iostream>
 3 #include<cstring>
 4 #include<cstdlib>
 5 #include<cstdio>
 6 #include<cmath>
 7 using namespace std;
 8 inline void Scan(int &x)
 9 {
10     char c;
11     while((c = getchar()) < '0' || c > '9');
12     x = c - '0';
13     while((c = getchar()) >= '0' && c <= '9') x = (x << 3) + (x << 1) + c - '0';
14 }
15 double eps = 1e-6;
16 int n, m;
17 double c[523];
18 double a[523][523];
19 int x[523], y[523];
20 int de[523];
21 double ans;
22 inline void Solve()
23 {
24     int now;
25     double t;
26     for(int i = 1; i <= n; ++i)
27     {
28         now = i;
29         while(fabs(a[i][now]) <= eps && now <= n) ++now;
30         if(now > n) continue;
31         for(int j = 1; j <= n + 1; ++j) swap(a[i][j], a[now][j]);
32         t = a[i][i];
33         for(int j = 1; j <= n + 1; ++j) a[i][j] /= t;
34         for(int j = 1; j <= n; ++j)
35             if(i != j)
36             {
37                 t = a[j][i];
38                 for(int k = 1; k <= n + 1; ++k)
39                     a[j][k] -= a[i][k] * t;
40             }
41     }
42 }
43 int main()
44 {
45     Scan(n), Scan(m);
46     for(int i = 1; i <= m; ++i)
47     {
48         Scan(x[i]), Scan(y[i]);
49         ++de[x[i]], ++de[y[i]];
50     }
51     for(int i = 1; i <= m; ++i)
52     {
53         a[x[i]][y[i]] += 1.0 / (double) de[y[i]];
54         a[y[i]][x[i]] += 1.0 / (double) de[x[i]];
55     }
56     for(int i = 1; i <= n + 1; ++i) a[n][i] = 0;
57     for(int i = 1; i <= n; ++i) a[i][i] = -1;
58     a[1][n + 1] = -1;
59     Solve();
60     for(int i = 1; i <= m; ++i)
61         c[i] = a[x[i]][n + 1] / (double) de[x[i]] + a[y[i]][n + 1] / (double) de[y[i]];
62     sort(c + 1, c + 1 + m);
63     for(int i = 1; i <= m; ++i)
64         ans += c[i] * (m - i + 1);
65     printf("%.3lf", ans);
66 }