在前面的文章中,使用了棧這一數據結構將通常使用的中綴表達式轉換成了後綴表達式,並再一次使用棧來對後綴表達式求值,從而計算出了表達式的值.
現在使用樹這一數據結構來將後綴表達式還原為中綴表達式.使用的是表達式樹.表達式樹是二叉樹的一種,所謂二叉樹,要麼它為為空樹,要麼不為空樹,並且每個節點最多有兩個孩子.而表達式樹則是二叉樹的一種,它的葉節點全為表達式中的數字,其余節點是運算符,即加,減,乘,除的運算符號.如圖所示,就是一棵表達式樹:
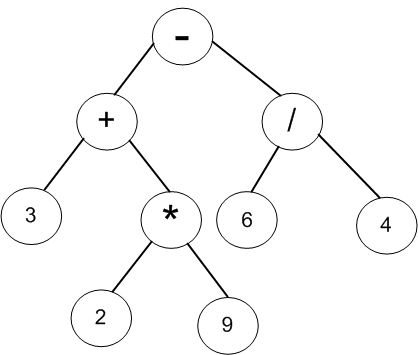
它的特點顯而易見.若我們對其進行先序遍歷(preorder),將獲得該表達式的前綴版本(前綴表達式):-+3*29/64;對其中序遍歷(inorder),得到中綴表達式:3+2*9-6/4;對其後序遍歷(postorder),得到後綴表達式:329*+64/-.
通過給出某個版本的表達式,可以構建一棵該表達式所對應的表達式樹.以後綴表達式為例,樹節點的結構如下:
1 struct EtreeNode
2 {
3 char value; //節點的值
4 EtreeNode *left; //指向左孩子
5 EtreeNode *right; //指向右孩子
6 };
構造一棵表達式樹,需要用到棧.算法與後綴表達式求值的算法很相似.若輸入是一個數字,創建一個節點指針,保存該數字,左右孩子指針皆為空(nullptr),將該節點指針壓棧;若輸入是運算符號,同樣的申請空間建立節點指針保存它,再從棧中彈出兩個節點指針作為該指針的左右孩子域.依次進行,直到輸入完結,彈棧,得到的是對應的表達式樹的根節點.
C++實現如下:
1 EtreeNode* creat_etree(const string &in) //構建表達式樹
2 {
3 if (!isdigit(in.at(0))) //第一個輸入若為運算符
4 {
5 try
6 {
7 ;
8 throw runtime_error("illegal expression");
9 }
10
11 catch (runtime_error err)
12 {
13 cout << err.what() << endl;
14 exit(EXIT_FAILURE);
15 } //第一個輸入若為運算符,拋出異常,程序結束運行
16 }
17
18 stack <EtreeNode*> ptrStack; //保存節點指針的棧
19
20 for (auto &i : in) //遍歷整個輸入字符串
21 {
22 if (isdigit(i)) //若為數字
23 {
24 EtreeNode *ptr = new EtreeNode;
25 ptr ->value = i;
26 ptr ->left = ptr ->right = nullptr;
27 ptrStack.push(ptr); //保存該數字並壓棧
28 }
29
30 else //為運算符
31 {
32 EtreeNode *b = ptrStack.top();
33 ptrStack.pop();
34
35 EtreeNode *a = ptrStack.top();
36 ptrStack.pop(); //彈出兩個數字
37
38 EtreeNode *ptr = new EtreeNode;
39
40 ptr ->value = i;
41 ptr ->left = a;
42 ptr ->right = b;
43 ptrStack.push(ptr); //指針指向兩個數字並壓棧
44 }
45 }
46
47 EtreeNode *root = ptrStack.top(); //彈出根節點
48 ptrStack.pop();
49
50 return root;
51 }
這樣,表達式樹構建完成,其根節點指針為root,通過其即可訪問整課表達式樹.需要什麼版本的表達式,就對其進行相應的遍歷.如進行中序遍歷得到中綴表達式:
1 void inorder_traversal(EtreeNode *r) //遞歸進行中序遍歷
2 {
3 if (r == nullptr)
4 return;
5
6 else
7 {
8 inorder_traversal(r ->left); //引用左子樹
9 cout << r ->value; //引用根節點
10 inorder_traversal(r ->right); //引用右子樹
11 }
12 }
這也是一種將後綴表達式轉換為中綴表達式的方法.
謝謝大家!轉載請注明出處,謝謝合作!