2016弱校聯盟十一專場10.3---Similarity of Subtrees（深搜+hash、映射），深搜和廣搜

2016弱校聯盟十一專場10.3---Similarity of Subtrees（深搜+hash、映射），深搜和廣搜

題目鏈接

https://acm.bnu.edu.cn/v3/problem_show.php?pid=52310

problem description

Define the depth of a node in a rooted tree by applying the following rules recursively:

      • The depth of a root node is 0.

      • The depths of child nodes whose parents are with depth d are d + 1.

Let S(T, d) be the number of nodes of T with depth d. Two rooted trees T and T ′ are similar if and only if S(T, d) equals S(T ′ , d) for all non-negative integer d. You are given a rooted tree T with N nodes. The nodes of T are numbered from 1 to N. Node 1 is the root node of T. Let Ti be the rooted subtree of T whose root is node i. Your task is to write a program which calculates the number of pairs (i, j) such that Ti and Tj are similar and i < j.

Input

The input consists of a single test case. N a1 b1 … aN−1 bN−1 The first line contains an integer N (1 ≤ N ≤ 100,000), which is the number of nodes in a tree. The following N − 1 lines give information of branches: the i-th line of them contains ai and bi , which indicates that a node ai is a parent of a node bi . (1 ≤ ai , bi ≤ N, ai ̸= bi) The root node is numbered by 1. It is guaranteed that a given graph is a rooted tree, i.e. there is exactly one parent for each node except the node 1, and the graph is connected.

Output

Print the number of the pairs (x, y) of the nodes such that the subtree with the root x and the subtree with the root y are similar and x < y. 14

Sample Input1

5

1 2

1 3

1 4

1 5

Output for the Sample Input 1

6

Sample Input2

6

1 2

2 3

3 4

1 5

5 6

Output for the Sample Input 2

2

Sample Input3

13

1 2

1 3

2 4

2 5

3 6

3 7

4 8

4 9

6 10

7 11

8 12

11 13

Output for the Sample Input 3

14

題意：輸入一棵由n個點和n-1條邊構成的樹，求這個樹中兩棵相似的子樹有多少對？ 相似的子樹：要求在相同的深度，兩顆子樹的在這一層的節點數相同；

思路：深搜，hash表示每一個點為子樹時的子樹狀態；

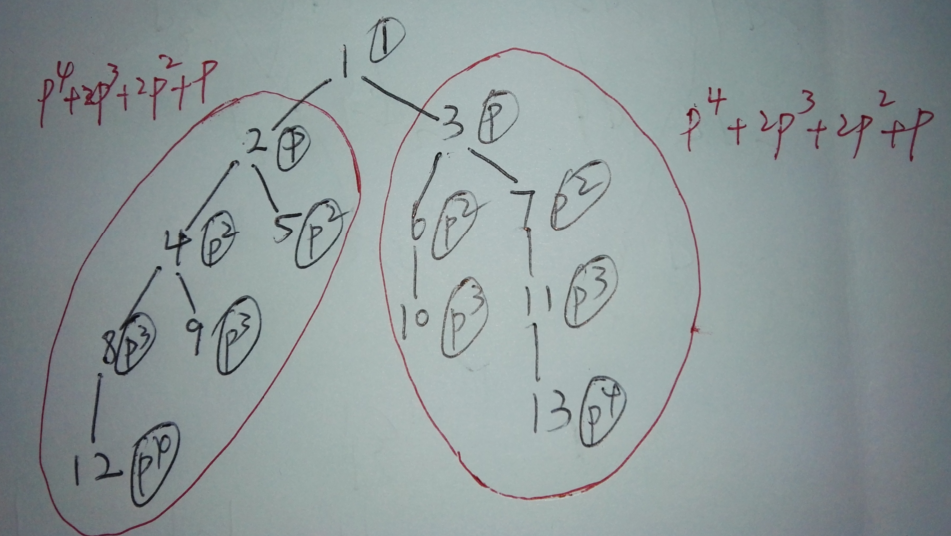
第三組樣例：對圖上每個點，給一個標識p^d d為這個點的深度，那麼每個點的子樹狀態就可以用子樹上所有項的和表示，如2號節點p^4+2p^3+2p^2+p   3號節點p^4+2p^3+2p^2+p 它們的多項式相同，為了方便用map映射統計，可以給p賦一個值，為了減小沖突可以取一個較大的質數，這就是hash；

代碼如下：

#include <iostream>
#include <stdio.h>
#include <queue>
#include <string.h>
#include <vector>
#include <map>
#include <string>
#include <set>
using namespace std;
typedef long long LL;
const LL maxn=1e6+10,p=9901,mod=1e9+7;
vector<LL>G[maxn];
LL hash_v[maxn];
map<LL,LL>mp;
map<LL,LL>::iterator it;

void dfs(LL u)
{
    hash_v[u]=1;
    for(LL i=0; i<G[u].size(); i++)
    {
        LL v=G[u][i];
        dfs(v);
        hash_v[u]=(hash_v[u]+hash_v[v]*p)%mod;
    }
    mp[hash_v[u]]++;
}
int main()
{
   ///freopen("in.txt","r",stdin);
    LL n;
    LL u,v;
    while(scanf("%lld",&n)!=-1)
    {
        for(LL i=0; i<=n; i++)
        G[i].clear();
        mp.clear();
        for(LL i=1; i<n; i++)
        {
            scanf("%lld%lld",&u,&v);
            G[u].push_back(v);
        }
        dfs(1);
        LL ans=0;
        for(it=mp.begin(); it!=mp.end(); it++)
            ans+=it->second*(it->second-1)/2;
        printf("%lld\n",ans);
    }
    return 0;
}