題目鏈接
https://acm.bnu.edu.cn/v3/problem_show.php?pid=52305
problem description
In ICPCCamp, there are n cities and (n−1) (bidirectional) roads between cities. The i-th road is between the ai-th and bi-th cities. It is guaranteed that cities are connected. Recently, there are 2×ci −1 new roads built between the ai-th and bi-th cities. Bobo soon comes up with an idea to travel around the world! He plans to start in city 1 and returns to city 1 after traveling along every road exactly once. It is clear that Bobo has many plans to choose from. He would like to find out the number of different plans, modulo (109 + 7). Note that two plans A and B are considered different only if there exists an i where the i-th traveled road in plan A is different from the i-th road in plan B.
Input
The first line contains an integer n (2 ≤ n ≤ 105 ). The i-th of the following (n − 1) lines contains 3 integers ai , bi , ci (1 ≤ ai , bi ≤ n, ci ≥ 1, c1 + c2 + · · · + cn−1 ≤ 106 ).
Output
An integer denotes the number of plans modulo (109 + 7).
Examples
standard input
3
1 2 1
2 3 1
3
1 2 1
1 3 2
standard output
4
144
題意:輸入n 表示由n個節點構成的樹,然後輸入n-1條邊,n-1行每行輸入ai bi c 表示ai點和bi點之間有2*c條邊相連,現在求從1號點開始走完所有邊且每條邊只走一次的方案數?
思路:深搜,然後排列組合,舉兩個例子:
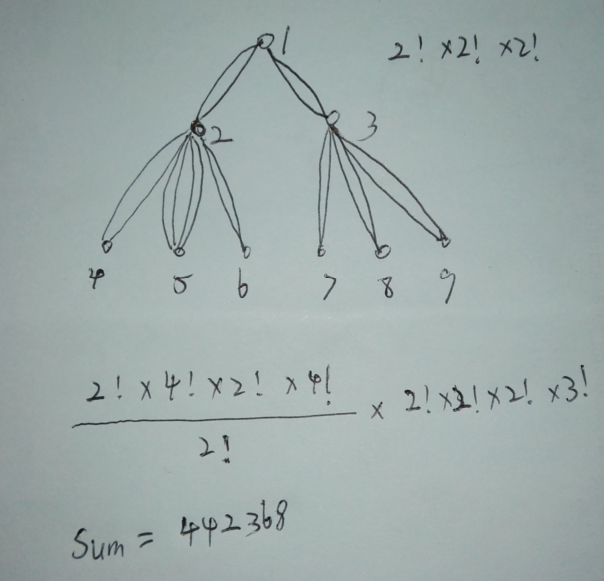
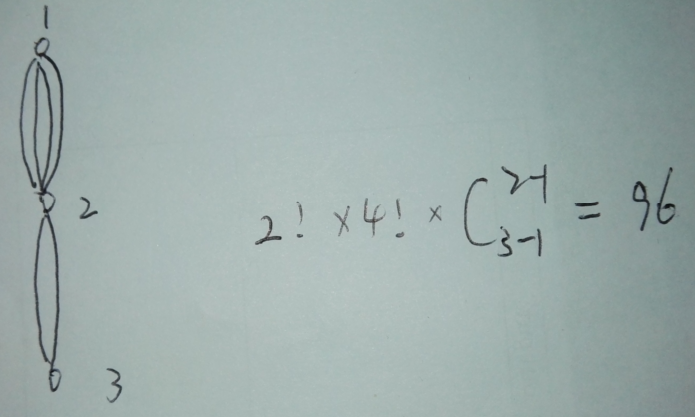
第一個圖片中:定義sum=1,從1號點開始向下深搜,到達孩子2號點的時候sum*=2! 表示從1到2號點走遍邊的方法數,然後繼續向下深搜到4號點,sum*=2! 然後返回再到5號點,sum*=4! 再返回走到6號點,sum*=2! ,然後返回2號點,這時sum*=4!/2! 為什麼呢? 因為從2號點開始走完它的直系(兒子)孩子節點時,它的兒子路徑之間存在先後順序,所以乘上路徑數的階乘,但要除去重復的部分比如從2號點到5號點時這兩條路徑的先後順序在之前的4!中已經考慮了,接下來就是相同的過程了......注意的是下面的孩子節點算完了,再計算上層節點時就不需要考慮了,但是相鄰兩層的節點之間還是有影響的,這個圖看不出來,我用下面一個圖作解釋。
第二個圖片中:按照之前的算法為sum=4!*2!=48 其實正確的解是96 ,少乘了一個2,為什麼呢? 因為上面一層的路徑對下面一層的路徑產生了影響,上一層有兩條路徑,下面一層只有一條路徑,那麼可以分析存在兩種情況:1、 1->2->3->2->1->2->1 2、 1->2->1->2->3->2->1 怎麼產生的? 其實是在走上一層的路徑時,在哪一次走的這一層的路徑,用擋板法,設上一層有t條路徑,這一層有s條路徑,那麼得在t次把下面的s條路徑走完,也就是C(t+s-1,t-1) 。
代碼如下:
#include <iostream>
#include <stdio.h>
#include <algorithm>
#include <string.h>
typedef long long LL;
const LL maxn=1e5+10;
const LL mod=1e9+7;
using namespace std;
struct Tree
{
LL to,next,c;
} edge[maxn*2];
LL Inv[30*maxn];
LL tot,head[maxn];
LL jc[maxn*30];
LL sum;
void Init()
{
Inv[0]=1;
Inv[1] = 1;
for(LL i=2; i<25*maxn; i++)
Inv[i] = (mod-mod/i)*Inv[mod%i]%mod;
for(LL i=2; i<25*maxn; i++)
Inv[i] = (Inv[i-1]*Inv[i])%mod;
}
void init()
{
tot=0;
memset(head,-1,sizeof(head));
}
void add_edge(LL u,LL v,LL c)
{
edge[tot].to=v;
edge[tot].c=c;
edge[tot].next=head[u];
head[u]=tot++;
}
void init2()
{
jc[0]=1;
for(LL i=1; i<maxn*30; i++)
jc[i]=((jc[i-1]*i)%mod);
}
LL road[maxn];
void dfs(LL u,LL pre)
{
road[u]=0;
for(LL i=head[u]; i!=-1; i=edge[i].next)
{
LL v=edge[i].to;
if(v==pre) continue;
dfs(v,u);
road[u]+=edge[i].c;
sum=(((sum*jc[edge[i].c*2])%mod)*Inv[edge[i].c])%mod;
sum=((sum* jc[(road[v]+edge[i].c-1)]%mod)*Inv[edge[i].c-1] )%mod;
sum=(sum*Inv[road[v]])%mod;
}
sum=(sum*jc[road[u]])%mod;
}
int main()
{
Init();
init2();
LL n,u,v,c;
while(scanf("%lld",&n)!=-1)
{
sum=1;
init();
for(LL i=1; i<n; i++)
{
scanf("%lld%lld%lld",&u,&v,&c);
add_edge(u,v,c);
add_edge(v,u,c);
}
dfs(1,0);
printf("%lld\n",sum);
}
return 0;
}