【小白入門向】tarjan算法+codevs1332題解報告,tarjancodevs1332
一、【前言】關於tarjan
tarjan算法是由Robert Tarjan提出的求解有向圖強連通分量的算法。
那麼問題來了找藍翔!(劃掉)什麼是強連通分量?
我們定義:如果兩個頂點互相連通(即存在A到B和B到A的通路),則稱這兩個點強連通。對於一個有向圖G,若是G中任意兩點都強連通,則稱G是一個強連通圖。有向圖的極大強連通子圖,稱為該圖的強連通分量。
對於下圖,{1,2,3,4}、{5}、{6}分別是它的強連通分量。
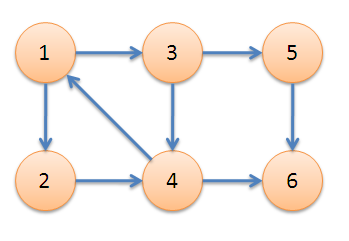
那麼tarjan是如何找到這些強連通分量的呢?
說白了tarjan就是dfs,每個強連通分量都是搜索樹中的一顆子樹。搜索時,我們把當前搜索樹中未處理過的點加入一個堆棧,回溯時從棧頂依次取出元素判斷他們是否屬於一個強連通分量。
我們對dfs的過程中添加如下定義:
1、dfn[i]:代表搜索點i的次序編號;
2、low[i]:代表點i所能回溯到的棧中最早的次序編號。
當dfn[i]=low[i]時,以i為根的子樹上的所有點便構成一個強連通分量。
二、tarjan算法c語言實現
那麼要如何使用程序來實現tarjan算法呢?
大致思路如下:
1、從一個未被處理過的點i開始,給它結合一個次序編號並把它壓入棧中,然後標記點表示其已入棧,令low[i]=dfn[i]=次序編號;
2、遍歷每條以i為起點的邊,若邊的終點j未被處理過,就對其進行操作1~3,令low[i]=min(low[i],low[j]);
3、找到的點j若是被處理過,則判斷其是否在棧中:若在,則令low[i]=min(low[i],dfn[j]);
4、若是dfn[i]=low[i],就將棧頂到i間的所有元素彈出,它們便是一個強連通分量;
5、重復1~4,直至不存在點未被處理。
貼上偽代碼(轉自百度百科詞條——tarjan算法)

![]()
1 tarjan(u)
2 {
3 DFN[u]=Low[u]=++Index//為節點u設定次序編號和Low初值
4 Stack.push(u)//將節點u壓入棧中
5 for each(u,v) in E//枚舉每一條邊
6 if (visnotvisted)//如果節點v未被訪問過
7 tarjan(v)//繼續向下找
8 Low[u]=min(Low[u],Low[v])
9 else if (vinS)//如果節點v還在棧內
10 Low[u]=min(Low[u],DFN[v])
11 if (DFN[u]==Low[u])//如果節點u是強連通分量的根
12 repeat{
13 v=S.pop//將v退棧,為該強連通分量中一個頂點
14 printv
15 until(u==v)
16 }
tarjan偽代碼
三、codevs1332題解
http://codevs.cn/problem/1332/←_←掛上原題鏈接
這是一道全♂裸的tarjan題,我們只需跑一遍tarjan,並對所有強連通分量染色,最後輸出最大的就好
代碼如下:

![]()
1 #include<stdio.h>
2 #include<algorithm>
3 using namespace std;
4 struct node
5 {
6 int v;
7 int next;
8 }e[50010];//鄰接表記錄有向圖
9 int stack[5010],top;//棧
10 int dfn[5010],low[5010],index;//index用於記錄次序編號
11 bool vis[5010];//判斷點是否在棧內
12 int st[5010],cnt;
13 int color[5010],s[5010],num;//用於染色並記錄顏色種類
14 void build(int a,int b)
15 {
16 e[++cnt].v=b;
17 e[cnt].next=st[a];
18 st[a]=cnt;
19 }//建圖,沒什麼好說的
20 void tarjan(int x)
21 {
22 dfn[x]=++index;
23 low[x]=index;
24 vis[x]=true;
25 stack[++top]=x;//當前點入棧
26 int i;
27 for(i=st[x];i!=0;i=e[i].next)//枚舉以當前點為起點的邊
28 {
29 int temp=e[i].v;//temp為當前被枚舉邊的終點
30 if(!dfn[temp])//如果當前邊終點未被處理
31 {
32 tarjan(temp);
33 low[x]=min(low[x],low[temp]);
34 }
35 else if(vis[temp])low[x]=min(low[x],dfn[temp]);
36 }
37 if(dfn[x]==low[x])
38 {
39 vis[x]=false;
40 color[x]=++num;//給當前強連通分量染上新顏色
41 s[num]++;//給當前強連通分量裡的點染色
42 while(stack[top]!=x)//棧頂元素依次出棧
43 {
44 s[num]++;
45 color[stack[top]]=num;
46 vis[stack[top--]]=false;
47 }
48 top--;
49 }
50 }
51 int main()
52 {
53 int n,m,i,a,b,t,ans=0,f;
54 scanf("%d%d",&n,&m);
55 for(i=1;i<=m;i++)
56 {
57 scanf("%d%d%d",&a,&b,&t);
58 build(a,b);
59 if(t-1)build(b,a);
60 }
61 for(i=1;i<=n;i++)
62 {
63 if(!dfn[i])tarjan(i);
64 }
65 for(i=1;i<=n;i++)
66 {
67 if(s[color[i]]>ans)//找到被染色最多的強連通分量(因為要求字典序,所以使用'>')
68 {
69 ans=s[color[i]];
70 f=i;
71 }
72 }
73 printf("%d\n",ans);
74 for(i=1;i<=n;i++)
75 {
76 if(color[i]==color[f])printf("%d ",i);//輸出被染成最大強連通分量的顏色的點
77 }
78 return 0;
79 }
CodeVs1332


