lower_bound和upper_bound算法，upper_bound

lower_bound和upper_bound算法，upper_bound

STL中的每個算法都非常精妙，接下來的幾天我想集中學習一下STL中的算法。

   ForwardIter lower_bound(ForwardIter first, ForwardIter last,const _Tp& val)算法返回一個非遞減序列[first, last)中的第一個大於等於值val的位置。

   ForwardIter upper_bound(ForwardIter first, ForwardIter last, const _Tp& val)算法返回一個非遞減序列[first, last)中第一個大於val的位置。

   lower_bound和upper_bound如下圖所示：

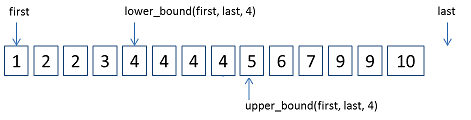
1， lower_bound

　　這個序列中可能會有很多重復的元素，也可能所有的元素都相同，為了充分考慮這種邊界條件，STL中的lower_bound算法總體上是才用了二分查找的方法，但是由於是查找序列中的第一個出現的值大於等於val的位置，所以算法要在二分查找的基礎上做一些細微的改動。

     首先是我修改數據結構課本上的二分查找實現的lower_bound算法：

int my_lower_bound(int *array, int size, int key)
{
    int first = 0, last = size-1;
    int middle, pos=0;       //需要用pos記錄第一個大於等於key的元素位置

    while(first < last)
    {
        middle = (first+last)/2;
        if(array[middle] < key){      //若中位數的值小於key的值，我們要在右邊子序列中查找，這時候pos可能是右邊子序列的第一個
            first = middle + 1;
            pos = first;
        }
        else{
            last = middle;           //若中位數的值大於等於key，我們要在左邊子序列查找，但有可能middle處就是最終位置，所以我們不移動last,
            pos = last;              //而是讓first不斷逼近last。
        }
    }
    return pos;
}

　　STL中的實現比較精巧，下面貼出源代碼：

//這個算法中，first是最終要返回的位置
int lower_bound(int *array, int size, int key)
{
    int first = 0, middle;
    int half, len;
    len = size;

    while(len > 0) {
        half = len >> 1;
        middle = first + half;
        if(array[middle] < key) {     
            first = middle + 1;          
            len = len-half-1;       //在右邊子序列中查找
        }
        else
            len = half;            //在左邊子序列（包含middle）中查找
    }
    return first;
}

2， upper_bound

upper_bound返回的是最後一個大於val的位置，也是有一個新元素val進來時的插入位置。

我依然將二分查找略做修改：

int my_upper_bound(int *array, int size, int key)
{
    int first = 0, last = size-1;
    int middle, pos = 0;

    while(first < last)
    {
        middle = (first+last)/2;
        if(array[middle] > key){     //當中位數大於key時，last不動，讓first不斷逼近last
            last = middle;
            pos = last;
        }
        else{
            first = middle + 1;     //當中位數小於等於key時，將first遞增，並記錄新的位置
            pos = first;
        }
    }
    return pos;
}

下面的代碼是STL中的upper_bound實現：

int upper_bound(int *array, int size, int key)
{
    int first = 0, len = size-1;
    int half, middle;

    while(len > 0){
        half = len >> 1;
        middle = first + half;
        if(array[middle] > key)     //中位數大於key,在包含last的左半邊序列中查找。
            len = half;
        else{
            first = middle + 1;    //中位數小於等於key,在右半邊序列中查找。
            len = len - half - 1;
        }
    }
    return first;
}