1.問題的提出
3名商人各帶1個隨從乘船渡河,一只小船只能容納2人,由他們自己劃行。在河的任何一岸當隨從的人數多於商人數時,商人就會有危險。但是如何乘船渡河的大權掌握在商人們手中,商人們怎樣才能安全渡河呢?
這就是著名的商僕渡河問題,對於這類智力游戲經過一番邏輯思索是可以找出解決辦法的。這裡要求將問題推廣至商僕對數任意、船只容量也任意的一般情況下,建立數學模型,並編程求解。
2.模型建立與符號說明
記商僕對數為m,船容量為c人。
記第k次渡河前此岸的商人數為xk,隨從數為yk,k=1,2,…,xk,yk=0,1,2,…,m,
將二維向量sk=(xk,yk)定義為狀態,安全渡河條件下的狀態集合定義為允許狀態空間,記做S
詳細問題描述見下圖:


這裡采用BFS算法(廣度優先搜索算法)編程求解商僕過河問題。BFS算法是最經典的圖搜索算法之一,在本題中可以保證找到的解為最短路徑,即所求方案過河總步數最少,其算法描述如下:
建立一個狀態隊列q,這是一個先進先出的隊列。
(1)將起始狀態即(n,n)點加入隊列q,標記(n,n)點為已訪問。
(2)將q的首節點出隊,再將所有該節點可達的未被訪問的允許狀態加入隊列q
(3)將所有新加入的狀態標記為已訪問,如果其中有終止狀態(0,0),則問題有解,算法結束。
(4)如果隊列q為空,則問題無解,算法結束。
(5)轉至(2)執行
分析:
觀察BFS算法的執行過程,算法首先將距離起始狀態為1次狀態轉移的所有狀態加入隊列,如果其中沒有終止狀態,則繼續將所有距離起始狀態為2次狀態轉移的狀態加入隊列……
由於隊列是先進先出的,可以始終保證所需狀態轉移步數最少的狀態排在隊列的最前部,並首先由他們擴展下一層狀態。
所以加入隊列的每個狀態都是以最短路徑(最少的狀態轉移步數)到達的,因為如果有更短的路徑存在,則此路徑上的狀態一定會被更早擴展,更早加入狀態隊列(所需步數少的狀態排在狀態隊列的前部)。
當終止狀態加入隊列時,到達終止狀態的路徑也是最短路徑,即求得一個所需狀態轉移步數最少的過河方案。
若某時刻狀態隊列為空且始終未到達終止狀態,則說明所有自起始狀態可達的節點均已被訪問,且其中沒有終止狀態,即終止狀態不可達,問題無解。
該問題商僕對數和船容量之間的關系與問題是否有解的分析:
商僕對數
小船容量
1、2、3
≥2
4、5
≥3
≥6
≥4
代碼:
#include <bits/stdc++.h>
#include "windows.h"
#define MAX_SIZE 1010
using namespace std;
struct CNode
{
int x;//x坐標
int y;//y坐標
int flag;//是否可以行走的點
int dir;//標記行船方向
CNode *p;//父節點指針
};
CNode G[MAX_SIZE][MAX_SIZE][2];//狀態空間 坐標,訪問
int V[MAX_SIZE][MAX_SIZE][2]; //訪問標記
deque <CNode> q;//搜索隊列
int num;//商僕對數
int cap;//船容量
bool solve;//解標記
int steps;//步數
void Init();//初始化
void BFS();//BFS搜索
void Output(CNode *p);//輸出
int main(){
Init();//進行初始化
while(!q.empty()&&!solve){//BFS搜索
BFS();
}
if(!solve)
cout<<"\n問題無解\n";
else{
cout<<"\n過河方案:\n";
Output(&G[0][0][1]);//回朔法輸出
cout<<"最少需要"<<steps<<"步\n";
}
return 0;
}
void Init(){
cout<<"共有商僕對數:";
cin>>num;
cout<<"船容量:";
cin>>cap;
int i,j;
for(int i = 0 ; i <= num ; i++){
for(int j = 0 ; j <= num ; j++){//初始化狀態空間
G[i][j][0].x = G[i][j][1].x = i;//坐標x
G[i][j][0].y = G[i][j][1].y = j;//坐標y
G[i][j][0].flag = G[i][j][1].flag = 0;//均初始化為不可行點為0
G[i][j][0].p = G[i][j][1].p = NULL;//結點
G[i][j][0].dir = -1;//行船方向左或者下
G[i][j][1].dir = 1;//行船方向右或者上
V[i][j][0] = V[i][j][1] = 0;//未訪問
}
}
for( i = 0 ; i <= num ; i++){//將可行點標記為1
G[0][i][0].flag = G[num][i][0].flag = G[i][i][0].flag = 1;
G[0][i][1].flag = G[num][i][1].flag = G[i][i][1].flag = 1;
}
G[num][num][0].flag = G[num][num][1].flag = 0 ;//右上角為初始狀態設置為0
solve = false;//標記問題有解與否
q.push_back(G[num][num][0]);//初始點進人隊列
steps = 0;//記錄下最少的渡河次數
}
void BFS(){
int x,y;//隊首所在坐標
int dx,dy;//變化坐標
int nx,ny;//行船後坐標
int dir;//行船方向
if(q.empty()||solve)//搜索隊列為空或者有解,退出搜索
return;
x=q.front().x;//取出隊首坐標
y=q.front().y;
dir=q.front().dir;
q.pop_front();//隊首出隊
for(dx = 0 ; dx <= cap ; dx++){
for(dy = 0 ; dy <= cap - dx; dy++){//枚舉所有可能的狀態
nx = x + dx * dir;
ny = y + dy * dir;
if(nx < 0 || nx > num || ny < 0 || ny > num )//坐標越界
continue;
if(G[nx][ny][0].flag == 0)//達到不可行點
continue;
if(dx == 0 && dy == 0)//坐標沒變化
continue;
if(dir > 0 && V[nx][ny][1] == 1)//該點被訪問過
continue;
if(dir < 0 && V[nx][ny][0] == 1)//該點被訪問過
continue;
if(dir>0){//放入隊列
G[nx][ny][0].p = &G[x][y][1];
q.push_back(G[nx][ny][0]);
}
else{//放入隊列
G[nx][ny][1].p = &G[x][y][0];
q.push_back(G[nx][ny][1]);
}
if(dir>0)//標記被訪問
V[nx][ny][1] = 1;
else
V[nx][ny][0] = 1;
if(nx == 0 && ny == 0){//達到終點
solve = true;
return;
}
}
}
}
void Output(CNode *p){//回溯法輸出遍歷結果
if(p -> p == NULL){
cout<<"("<<p->x<<","<<p->y<<")\n";
return;
}
Output(p->p);
cout<<"("<<p->x<<","<<p->y<<")\n";
steps++;
}
/*
- - - - - - - - - - - - - - - - - -
3對
* *
** *
* *
4對
* *
* * *
** *
* *
5對
* *
* **
* * *
** *
* *
6對
* *
* **
* * *
* * *
** *
* *
n對 圖形為 N
*/
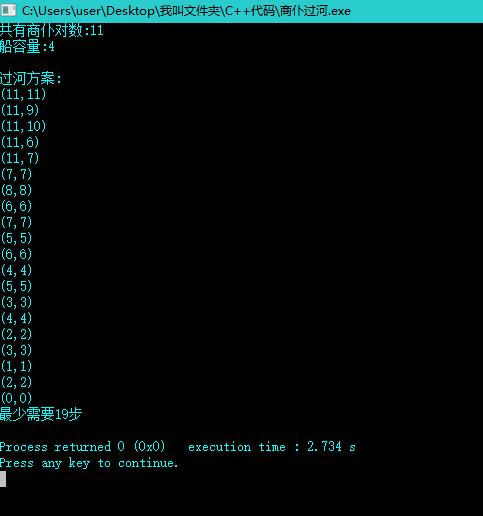
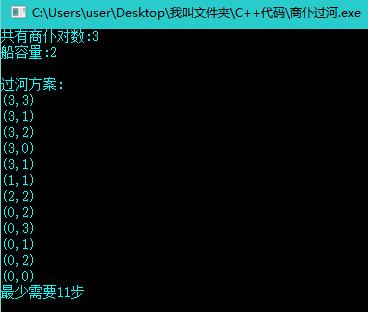
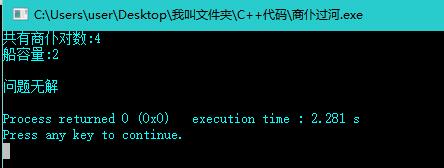
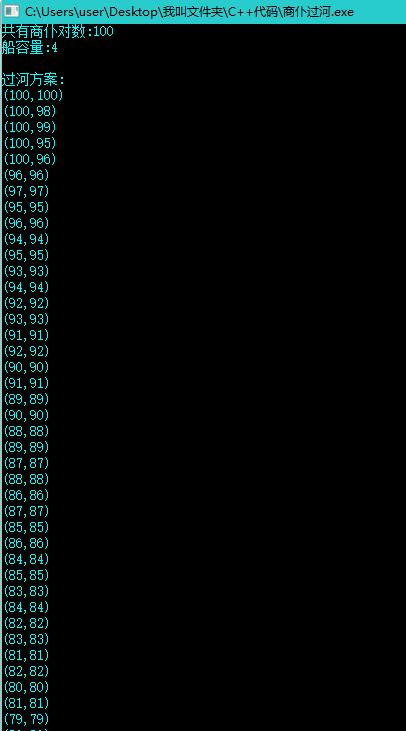
運行截圖: