Kruskal算法，kruskal

Kruskal算法，kruskal

1、基本思想：設無向連通網為G＝(V, E)，令G的最小生成樹為T＝(U, TE)，其初態為U＝V，TE＝{ }，然後，按照邊的權值由小到大的順序，考察G的邊集E中的各條邊。若被考察的邊的兩個頂點屬於T的兩個不同的連通分量，則將此邊作為最小生成樹的邊加入到T中，同時把兩個連通分量連接為一個連通分量；若被考察邊的兩個頂點屬於同一個連通分量，則捨去此邊，以免造成回路，如此下去，當T中的連通分量個數為1時，此連通分量便為G的一棵最小生成樹。 
2、示例：

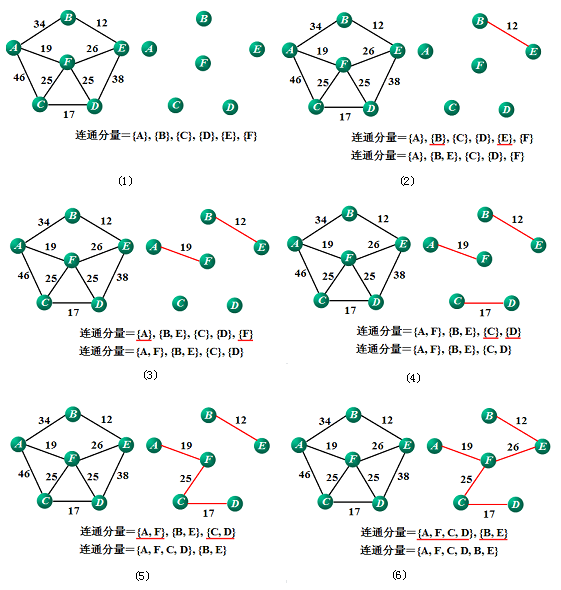
3、代碼實現如下：

1. #include "stdio.h"  
2. #include "stdlib.h"  
3. struct edge  
4. {  
5.     int m;  
6.     int n;  
7.     int d;  
8. }a[5010];  
9. int cmp(const void *a,const void *b) //按升序排列  
10. {  
11.     return ((struct edge *)a)->d>((struct edge *)b)->d;  
12. }  
13. int main(void)  
14. {  
15.     int i,n,t,num,min,k,g,x[100];  
16.     printf("請輸入頂點的個數：");  
17.     scanf("%d",&n);  
18.     t=n*(n-1)/2;  
19.     for(i=1;i<=n;i++)  
20.         x[i]=i;  
21.     printf("請輸入每條邊的起始端點、權值：/n");  
22.     for(i=0;i<t;i++)  
23.         scanf("%d %d %d",&a[i].m,&a[i].n,&a[i].d); //輸入每條邊的權值  
24.     qsort(a,t,sizeof(a[0]),cmp);  
25.     min=num=0;  
26.     for(i=0;i<t && num<n-1;i++)  
27.     {  
28.         for(k=a[i].m;x[k]!=k;k=x[k])  //判斷線段的起始點所在的集合  
29.             x[k]=x[x[k]];  
30.         for(g=a[i].n;x[g]!=g;g=x[g])  //判斷線段的終點所在的集合  
31.             x[g]=x[x[g]];  
32.         if(k!=g)  //如果線段的兩個端點所在的集合不一樣  
33.         {  
34.             x[g]=k;  
35.             min+=a[i].d;  
36.             num++;  
37.             printf("最小生成樹中加入邊：%d %d/n",a[i].m,a[i].n);  
38.         }  
39.     }  
40.     printf("最小生成樹的權值為：%d/n",min);  
41.     system("pause");  
42.     return 0;  
43. }