最近因為要寫機械臂的運動學控制程序，因此難免就要在C++中進行矩陣運算。然而C++本身不支持矩陣運算，Qt庫中的矩陣運算能力也相當有限，因此考慮尋求矩陣運算庫Eigen的幫助。
Eigen是一個C++線性運算的模板庫：他可以用來完成矩陣，向量，數值解等相關的運算。（Eigen is a C++ template library for linear algebra: matrices, vectors, numerical solvers, and related algorithms.）
Eigen庫下載： http://eigen.tuxfamily.org/index.php?title=Main_Page
Eigen庫的使用相當方便，將壓縮包中的Eigen文件夾拷貝到項目目錄下，直接包含其中的頭文件即可使用，省去了使用Cmake進行編譯的煩惱。
Eigen官網有快速入門的參考文檔：http://eigen.tuxfamily.org/dox/group__QuickRefPage.html
基本的矩陣運算只需要包含Dense即可
聲明：
#include<Eigen/Dense> ... //1D objects Vector4d v4; Vector2f v1(x, y); Array3i v2(x, y, z); Vector4d v3(x, y, z, w); VectorXf v5; // empty object ArrayXf v6(size); //2D objects atrix4f m1; MatrixXf m5; // empty object MatrixXf m6(nb_rows, nb_columns);
賦值：
//
Vector3f v1; v1 << x, y, z;
ArrayXf v2(4); v2 << 1, 2, 3, 4;
//
Matrix3f m1; m1 << 1, 2, 3,
4, 5, 6,
7, 8, 9;
int rows=5, cols=5;
MatrixXf m(rows,cols);
m << (Matrix3f() << 1, 2, 3, 4, 5, 6, 7, 8, 9).finished(),
MatrixXf::Zero(3,cols-3),
MatrixXf::Zero(rows-3,3),
MatrixXf::Identity(rows-3,cols-3);
cout << m;
//對應的輸出：
1 2 3 0 0
4 5 6 0 0
7 8 9 0 0
0 0 0 1 0
0 0 0 0 1
Resize矩陣：
// vector.resize(size); vector.resizeLike(other_vector); vector.conservativeResize(size); // matrix.resize(nb_rows, nb_cols); matrix.resize(Eigen::NoChange, nb_cols); matrix.resize(nb_rows, Eigen::NoChange); matrix.resizeLike(other_matrix); matrix.conservativeResize(nb_rows, nb_cols);
元素讀取：
vector(i)； vector[i]； matrix(i,j)；
矩陣的預定義：
//vector x
x.setZero();
x.setOnes();
x.setConstant(value);
x.setRandom();
x.setLinSpaced(size, low, high);
VectorXf::Unit(4,1) == Vector4f(0,1,0,0)
== Vector4f::UnitY()
//matrix x
x.setZero(rows, cols);
x.setOnes(rows, cols);
x.setConstant(rows, cols, value);
x.setRandom(rows, cols);
x.setIdentity();//單位矩陣
x.setIdentity(rows, cols);
映射操作，可以將c語言類型的數組映射為矩陣或向量：
（注意：
1.映射只適用於對一維數組進行操作，如果希望將二維數組映射為對應的矩陣，可以借助"mat.row(i)=Map<Vector> v(data[i],n)"進行循環來實現，其中data為二維數組名，n為數組第一維的維度。
2.應設置之後數組名和矩陣或向量名其實指向同一個地址，只是名字和用法不同，另外，對其中的任何一個進行修改都會修改另外一個）
//連續映射
float data[] = {1,2,3,4};
Map<Vector3f> v1(data); // uses v1 as a Vector3f object
Map<ArrayXf> v2(data,3); // uses v2 as a ArrayXf object
Map<Array22f> m1(data); // uses m1 as a Array22f object
Map<MatrixXf> m2(data,2,2); // uses m2 as a MatrixXf object
//間隔映射
float data[] = {1,2,3,4,5,6,7,8,9};
Map<VectorXf,0,InnerStride<2> > v1(data,3); // = [1,3,5]
Map<VectorXf,0,InnerStride<> > v2(data,3,InnerStride<>(3)); // = [1,4,7]
Map<MatrixXf,0,OuterStride<3> > m2(data,2,3); // both lines |1,4,7|
Map<MatrixXf,0,OuterStride<> > m1(data,2,3,OuterStride<>(3)); // are equal to: |2,5,8|
算術運算：
add
norm
cross product * #include <Eigen/Geometry> vec3 = vec1.cross(vec2);
Coefficient-wise operators for matrices and vectors:
Array operators:*
Arithmetic operators array1 * array2 array1 / array2 array1 *= array2 array1 /= array2 array1 + scalar array1 - scalar array1 += scalar array1 -= scalar Comparisons array1 < array2 array1 > array2 array1 < scalar array1 > scalar array1 <= array2 array1 >= array2 array1 <= scalar array1 >= scalar array1 == array2 array1 != array2 array1 == scalar array1 != scalar Trigo, power, and
Eigen provides several reduction methods such as: minCoeff() , maxCoeff() , sum() , prod() , trace() *, norm()*, squaredNorm() *, all() , and any() . All reduction operations can be done matrix-wise, column-wise or row-wise. Usage example:
5 3 1 mat = 2 7 8 9 4 6 mat.minCoeff(); 1 mat.colwise().minCoeff(); 2 3 1 mat.rowwise().minCoeff(); 1 2 4Typical use cases of all() and any():
//Typical use cases of all() and any(): if((array1 > 0).all()) ... // if all coefficients of array1 are greater than 0 ... if((array1 < array2).any()) ... // if there exist a pair i,j such that array1(i,j) < array2(i,j) ...
Read-write access to a column or a row of a matrix (or array):
mat1.row(i) = mat2.col(j); mat1.col(j1).swap(mat1.col(j2));Read-write access to sub-vectors:
n coeffs
vec1.tail(n)
vec1.tail<n>()
the last n coeffs
vec1.segment(pos,n)
vec1.segment<n>(pos)
the n coeffs in the pos : pos + n - 1]
Read-write access to sub-matrices:
mat1.block(i,j,rows,cols) (more) mat1.block<rows,cols>(i,j) (more) therows x cols sub-matrix i,j)
mat1.topLeftCorner(rows,cols)
mat1.topRightCorner(rows,cols)
mat1.bottomLeftCorner(rows,cols)
mat1.bottomRightCorner(rows,cols)
mat1.topLeftCorner<rows,cols>()
mat1.topRightCorner<rows,cols>()
mat1.bottomLeftCorner<rows,cols>()
mat1.bottomRightCorner<rows,cols>()
the rows x cols sub-matrix top
Vectors, rows, and/or columns of a matrix can be reversed (see DenseBase::reverse(), DenseBase::reverseInPlace(),VectorwiseOp::reverse()).
vec.reverse() mat.colwise().reverse() mat.rowwise().reverse() vec.reverseInPlace()Vectors, matrices, rows, and/or columns can be replicated in any direction (see DenseBase::replicate(),VectorwiseOp::replicate())
vec.replicate(times) vec.replicate<Times> mat.replicate(vertical_times, horizontal_times) mat.replicate<VerticalTimes, HorizontalTimes>() mat.colwise().replicate(vertical_times, horizontal_times) mat.colwise().replicate<VerticalTimes, HorizontalTimes>() mat.rowwise().replicate(vertical_times, horizontal_times) mat.rowwise().replicate<VerticalTimes, HorizontalTimes>()top
(matrix world *)
Optimized products and inverse mat3 = scalar * diag1 * mat1; mat3 += scalar * mat1 * vec1.asDiagonal(); mat3 = vec1.asDiagonal().inverse() * mat1 mat3 = mat1 * diag1.inverse()
TriangularView gives a view on a triangular part of a dense matrix and allows to perform optimized operations on it. The opposite triangular part is never referenced and can be used to store other information.
template keyword if it is used on an object of a type that depends on a template parameter; see The template and typename keywords in C++ for details.Xxx = Upper, Lower, StrictlyUpper, StrictlyLower, UnitUpper,UnitLower
Writing to a specific triangular part: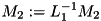
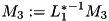
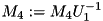
Just as for triangular matrix, you can reference any triangular part of a square matrix to see it as a selfadjoint matrix and perform special and optimized operations. Again the opposite triangular part is never referenced and can be used to store other information.
template keyword if it is used on an object of a type that depends on a template parameter; see The template and typename keywords in C++ for details.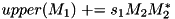
)
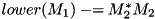
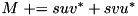M.selfadjointView<Eigen::Upper>().rankUpdate(u,v,s);
Solving linear equations:
)
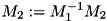// via a standard Cholesky factorization
m2 = m1.selfadjointView<Eigen::Upper>().llt().solve(m2);
// via a Cholesky factorization with pivoting
m2 = m1.selfadjointView<Eigen::Lower>().ldlt().solve(m2);
