博弈,博弈論
所謂博弈,就是兩人輪流進行決策,並且兩人都使用最優策略來獲取勝利。通俗的說就是兩個人都想獲得勝利,兩個人都有頭腦,並且不會失誤。博弈的次數是有限的,兩人遵循的規則是相同的。
1.巴什博弈
有一堆石子,共有n塊,兩個人輪流取石子,每次至少取1塊,最多取m個,最後取光者獲勝(假設A,B兩個人,規定A先操作)。
(1)當n=(m+1)*k時,(k為任意正整數),當A先取石子時,A取X塊石子,無論X為多少,B只要取(m+1-x),則B必勝,此時為A的必敗態。
(2)當n=(m+1)*k+r(k,r為任意正整數,r不大於m),此時A先取r塊,那麼B始終處在(m+1)*k的狀態,由(1)可知,此時A一定贏,為A的必勝態。
通過以上就可以變形從而解決很多問題。。
例1:假設有一個箱子,可以裝n個物品,每次最多可以裝m個,最少可以裝1個,A,B輪流操作,最後裝滿箱子的人獲勝。
偽代碼如下:
if(n%(m+1))
A獲勝
else
B獲勝
例2:
假設一堆有n個物品,每次最多取m個,最少取1個,最後取光者輸(A先進行)
偽代碼:
if((n-1)%(m+1)==0)
B 獲勝
else
A獲勝
看完基本原理刷幾道水題吧,啊哈哈。。。
HDU1846 http://acm.hdu.edu.cn/showproblem.php?pid=1846
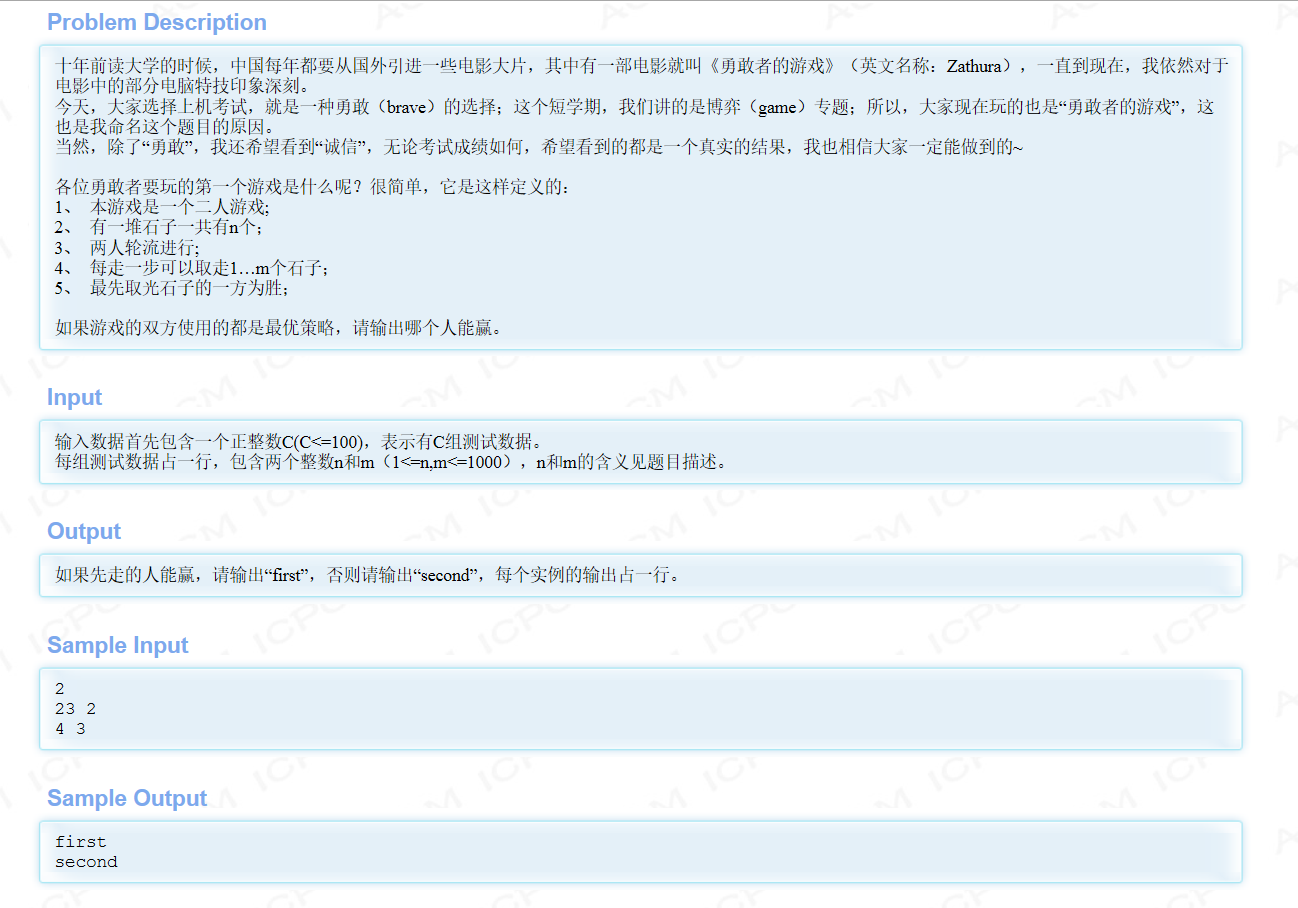
代碼如下:

![]()
1 #include<stdio.h>
2 #include<algorithm>
3 #include<iostream>
4 using namespace std;
5 int main()
6 {
7 int t,m,n;
8 cin>>t;
9 while(t--){
10 cin>>n>>m;
11 if(n%(m+1))
12 cout<<"first"<<endl;
13 else cout<<"second"<<endl;
14 }
15 }
View Code
這個是最基本的啦,直接套模板。
再看一個題吧
HDU1847 http://acm.hdu.edu.cn/showproblem.php?pid=1847
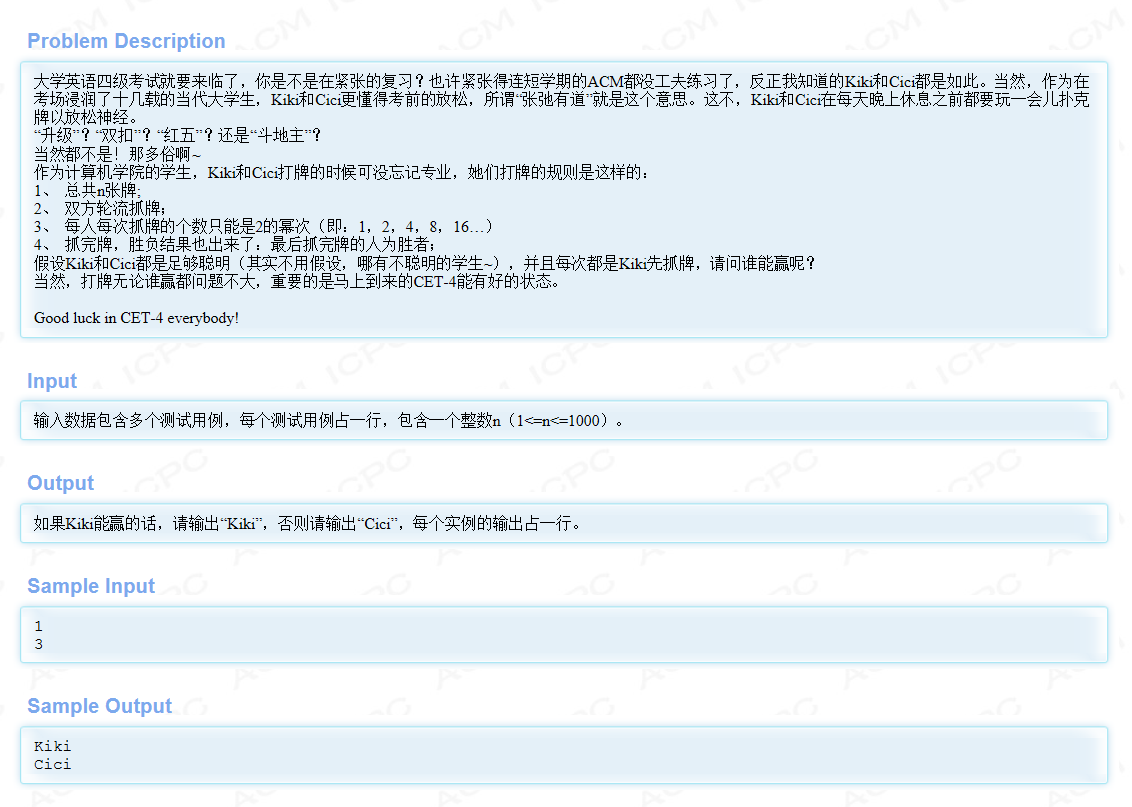
這個題就是在巴什博弈的模板的基礎上小小的改動啦一下,思考一下就好啦。。
題目說每次取牌的數目只能是2的冪數,且每次Kiki先開始取牌,我們從特殊情況開始討論
1.當牌數n就是2的冪數的時候,Kiki直接拿走所有的牌,此時Kiki獲勝。
2.當牌數n不是恰好是2的冪數,這個時候如果把牌分成x個部分,每個部分都是由2的冪數組成,那麼如果x為奇數,就是Kiki贏,否則就是Cici贏。
思路理解啦,咱們來看代碼吧,這個思路是從學長那裡借鑒來的,哈哈!!!!!!!!!!

![]()
1 #include<stdio.h>
2 #include<iostream>
3 #include<string.h>
4 #include<algorithm>
5 using namespace std;
6 const int maxn=1005;
7 bool used[maxn];
8 void check()
9 {
10 int n;
11 memset(used,false,sizeof(used));
12 for(int i=0;i<maxn;i++){
13 if(!used[i]){
14 int shu=1;
15 while(shu+i<maxn){
16 used[shu+i]=true;
17 shu<<=1;
18 }
19 }
20 }
21
22 }
23 int main(){
24 check();
25 int m;
26 while(cin>>m){
27 if(used[m]){
28 cout<<"Kiki"<<endl;
29
30 }
31 else
32
33 cout<<"Cici"<<endl;
34 }
35 }
View Code
針對這道題,還有另外一種想法。。
題目說的是2的冪次,那麼如果每次留給對手的都是3的倍數的話,對手如果取1,你就可以再取一點點,仍然留給對手3的倍數,如果對手取2的冪次,那麼你就直接取1啦嘛。。
代碼如下:

![]()
1 #include<stdio.h>
2 #include<iostream>
3 #include<algorithm>
4 #include<string.h>
5 using namespace std;
6 int main(){
7 int n;
8 while(cin>>n){
9 if(n%3==0)
10 cout<<"Cici"<<endl;
11
12
13 else cout<<"Kiki"<<endl;
14 }
15 }
View Code




