第一次嘗試寫動態規劃(Dynamic Planning) = =
問題如下:
-------------------------------------------------------------------------------------------------------------------------
最小代價子母樹
設有一排數,共n個,例如:22 14 7 13 26 15 11.任意2個相鄰的數可以進行歸並,歸並的代價為該兩個數的和,經過不斷的歸並,最後歸為一堆,而全部歸並代價的和稱為總代價,給出一種歸並算法,使總代價為最小.
輸入、輸出數據格式與“石子合並”相同。
輸入樣例:
4
12 5 16 4
-------------------------------------------------------------------------------------------------------------------------
為了說明算法的過程,我們先分析一些簡單的情況:
1·把序列的n個數,看成二元樹的葉子(二叉樹)的權。如果用一種括號把兩個正整數括起來,則它們對應結點的父輩的權就是由這次加法產生的中間和。這樣就把對序列任何一種加括號的方法與一棵帶權的二元樹對應。上面例子中加括號方法對應二元樹如圖
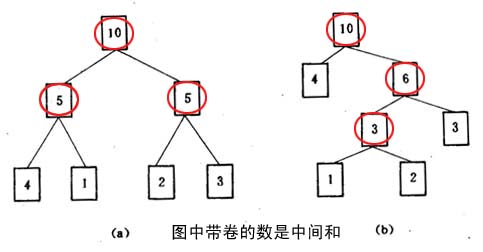
一棵帶權二元樹的代價就是樹中所有根結點權之和。代價最小的帶權二元樹稱為最優二元樹。問題轉化為求最優帶權二元樹。
那麼,什麼是最優帶權二元樹呢?
最優二叉樹,又稱哈夫曼樹,是一類帶權路徑長度最短的樹,有著廣泛的應用。
我們首先給出路徑和路徑長度的概念。從樹中一個結點到另一個結點之間的分支構成這兩個結點之間的路徑,路徑上的分支數目稱做路徑長度。樹的路徑長度是從樹根到每一結點的路徑長度之和。這種路徑長度最短的二叉樹是。
若將上述概念推廣到一般情況,考慮帶權的結點。結點的帶權路徑長度為從該結點樹根之間的路徑長度與結點上權的乘積。樹的帶權路徑長度為樹中所有葉子結點的帶路徑長度之和,通常記作
WPL=∑W(k)L(k) k=1...n
假設有n個權值W(1),W(2),......,W(n),試構造一棵有n個葉子結點的二叉樹,每個葉子結點帶權為W(k),則其中帶權路徑長度WPL最小的二叉樹稱做最優二又樹或哈夫顯樹。
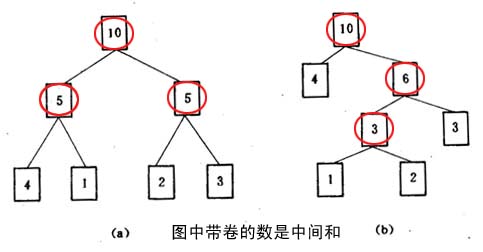
例如,圖中的兩棵二叉樹,都有4個葉子結點a、b、c、d,分別帶權4,1,2,3,它們的帶權路徑長度分別為
(a)WPL=4×2十1×2十2×2十3×2=20
(b)WPL=4×1十1×3十2×3十3×2=19
如何構造哈夫曼樹呢?俗稱哈夫曼算法。現敘述如下:
(1)根據給定的n個權值W(1),W(2),......,W(n)構成n棵二叉樹的集合F={T(1),T(2),......,T(n)}
其中每棵二叉樹T(k)中只有一個帶權為W(k)的根結點,其左右子樹均空。
(2)在F中選取兩棵根結點的權值最小的樹作為左右子樹構造一棵新的二叉樹,且置新的二叉樹的根結點的權值為其左、右子樹上根結點的權值之和。
(3)在F中刪除這兩棵樹,同時將新得到的二叉樹加入F中。
(4)重復(2)和(3),直到F只含一棵樹為止。這棵樹便是哈夫曼樹。
2·如果一棵帶權的二元樹是最優的,那末它的任何一棵子樹對於這棵子樹的樹葉來說也是最優的。因此,帶權最優二元樹的問題符合最優化原則。可以用動態歸劃方法求解。
3·對於這個問題在決策時要考慮到樹葉序列的劃分方案。
[狀態分析]
1·從序列4,4,8,5,4,3,5分析它的二元權的結構。圖給出兩棵二元樹(a)、(b)。
tu29.JPG (21617 bytes)
這棵7片葉葉的二元樹,圖(a)中的樹的左子樹是三片葉子,右子樹是4片葉子,對應於樹葉的一種劃分方案。記為(左3,右4)。對應添號形式是:(4+4)+8)+((5+4)+(3+5)))其代價和為91。
圖(b)對應於另一種劃分方案記為(左4,右3),其代價和是94。可見,由於樹葉的劃分方案不同,所得的二元樹的代價也不同。對七片葉子的二元樹,可以有
(左1,右6),(左2,右5),(左3,右4),(左4,右3),(左5,右2),(左6,右1)六種劃分方法,對於每一種劃分方法都對元一棵二元樹,從中找出最優的二元樹。
2·決策的前提是最優化原理。對於每一種劃分方案,比如(左3,右4),應該知道前三數4,4,8作為樹葉構成最優的子二元樹是什麼,也應知道5,4,3,5作為樹葉構成最優二元樹的最優子二元樹是什麼。根據最優化原理,由這棵最優子二元樹合成的二元樹一定是對於(左3,右4)劃分方案最優二元樹。從此可見,二元樹的構成中每一步的決策不僅與前一步決定有關,而且與若干步的決策有關。二元樹的代價計算是一個遞推過程。我們選用序列4,4,8,5,4,3,5把它可能構成的各類帶權二元樹的代價與權的遞推計算方法表示如圖中。
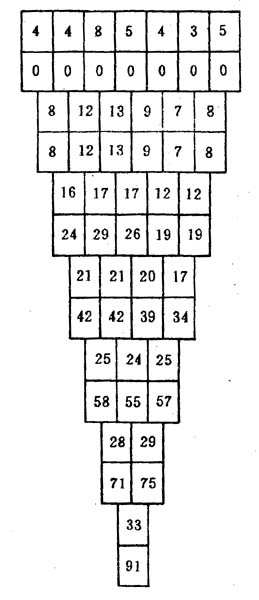
計算方法說明如下,
[1]一片樹葉權重為葉片的權,代價為0,得圖的第一層。
[2]二片樹葉。它的構成狀態共有:(4,4),(4,8),(8,5),(5,4),(4,3),(3,5)共六種。括號內數字之和是中間和即為子樹根的權。於是生成2片樹葉權重。因為1片樹葉權為0,故2片的代價與權重一樣。
[3]三片樹葉,它的構成狀態有:(4,4,8),(4,8,5),(8,5,4),(5,4,3),(4,3,5)共計5種。於是生成二片樹葉的權。代價計算時應考慮3片樹葉的劃分狀態可能(左1,右2)或(左2,右1),3片樹葉的代價應考慮它們代價中的最小者。若是對(4,4,8)進行劃分時其狀態有:
(1)以(左1,右2)劃分時其狀態有(4),(4,8),其中(4)的代價為0,(4,8)代價為12。代價和為12=0+12。
(2)以(左2,右1)劃分時其狀態有(4,4),(8),其中(4,4)的代價為8,8的代價為0。代價和為8。
因為8比12小,3片樹葉4,4,8的代價是它的權加上劃分狀態中代價小的。於是得出第一個代價為16+8=24。余類推。
[4]四片樹葉時,不難算出其權重為21,21,20,17。代價計算應考慮前面劃分的可能情況。以樹葉權重為4,4,8,5為例。它的劃分方法有:
(左1,右3),(左2,右2),(左3,右1)三種。
把每一種劃分的代價計算如下:
(1)以(左1,右3)劃分狀態是:(4),(4,4,5),其中(4)的代價為0,(4,4,5)代價為29,0+29=29(代價和)。
(2)以(左2,右2)劃分狀態是:(4,4),(8,5),其中(4,4)的代價為8,(8,5)代價為13,8+13二21(代價和)。
(3)以(左3,右1)劃分狀態是:(4,4,8),(5),其中(4,4,8)的代價24,(5)的代價為0,24十0二24(代價和)。
這三種劃分狀態代價和最小的是21。於是4片中4,4,8,5的權為21。代價為21+21=42。其他代價可仿此計算。
[5]五片樹葉時,權重不難算出。代價計算應考慮劃分:
(左1,右4),(左2,右3),(左3,右2),(左4,右1)的代價。
當權重為25,樹葉是4,4,8,5,4。
劃分(左1,右4)的狀態是(4),(4,8,5,4),代價和為0+42=42。
劃分(左2,右3)的狀態是(4,4),(8,5,4),代價和為8+26=34。
因為8,5,4是三片葉子中第三個,從3片樹葉的代價中查到26。
劃分(左3,右2)的狀態是(4,4,8),(5,4)。由圖中查得代價和為24+9=33。
劃分(左4,右1)的狀態是(4,4,8,5),(4),由圖中查得代價和為42+0=42。
於是關於權重為25,樹葉為4,4,8,5,4的代價為25+33=58。
當權重為24,樹葉為4,8,5,4,3。
劃分(左1,右4)代價為0+39=39
劃分(左2,右3)代價為12+19=31
劃分(左3,右2)代價為29+7=36
劃分(左4,右1)代價為42+0=42
31是最小代價,權重為24,於是得代價為31+24=55。
當權重為25,樹葉為8,5,4,3,5按劃分計算可得其代價為57。
其他的計算由讀者去完成。
從以上分析,帶權二元樹的代價計算是一個比較復雜的遞推過程。高層的代價計算,必須用本身的劃分狀態,利用底層的代價進行計算。雖然遞推關系比較復雜,對大多數問題來說,動態規劃算法的復雜性有可能是多項式級的。動態規劃是一個很有實用價值的用途甚廣的組合算法。
剛開始犯了很多錯,
比如先開始是這麼寫的(一臉蒙蔽):
1 for (int i=1;i<=n;i++) 2 for (int j=i+1;j<=n;j++) 3 for (int k=i;k<=j-1;k++) 4 f[i][j]=(f[i][j]>f[i][k]+f[k+1][j]+g[i][j])?f[i][k]+f[k+1][j]+g[i][j]:f[i][j];//未考慮遞推關系
手動揮手.jpg
正解如下:
1 #include "iostream"
2 #include "cstdio"
3 #include "queue"
4 #define qwq 21000000
5 int n,m,q;
6 using namespace std;
7 int f[1000][1000];
8 int g[1000][1000];
9 int gra[1000],minn=-2100000;
10 int main()
11 {
12 int n;
13 cin>>n;
14 for (int i=1;i<=n;i++)
15 cin>>gra[i];
16
17 for (int i=1;i<=n;i++)
18 g[i][i]=gra[i];
19
20 for (int i=1;i<=n;i++)
21 for (int j=i+1;j<=n;j++)
22 g[i][j]=g[i][j-1]+gra[j];
23
24 for (int i=1;i<=n;i++)
25 for (int j=1;j<=n;j++)
26 f[i][j]=(i!=j)?qwq:0; //i -> j(i)的代價為 +∞(0)
27
28 for (int p=2;p<=n;p++)//窮舉堆數//因為是遞推(Recursion)所以從小堆數向大堆數
29 for (int i=1;i<=(n-p+1);i++)//一段的確定性(Certainty) 列舉起點
30 {
31 int j=i+p-1; //終點(Destination)
32 for (int k=i;k<=j-1;k++)//窮舉隔開位置 //注意超界所致的溢出(Overflow)
33 f[i][j]=(f[i][j]>f[i][k]+f[k+1][j]+g[i][j])?f[i][k]+f[k+1][j]+g[i][j]:f[i][j];//三目運算符不清楚的可以百度,下面也有簡介
34 } //正確寫出狀態轉移方程//無後效性 (Unfollow-up Effect)
35 cout<<f[1][n]<<endl;
36 }
動態規劃真的是個神奇的東西,
它適合求解多階段(狀態轉換)決策問題的最優解,也可用於含有線性或非線性遞推關系的最優解問題。
但其實它並不全能,
1,最優化原理
2,無後效性
必須滿足這兩個條件才能用,
當然,
寫動態規劃最主要的是寫出狀態轉移方程,
其次是邊界條件。
附一:
三目運算符普遍的用處就是減少if語句的使用
例如:
1 i=(括號條件成立與否)?(成立):(不成立);