C++實用數據結構：二叉索引樹，數據結構二叉

C++實用數據結構：二叉索引樹，數據結構二叉

看下面這個問題（動態連續和查詢）：

有一個數組A（長度為n），要求進行兩種操作： add(i,x)：讓A_i增大x； query(a,b)：詢問A_a+A_a+1+...+A_b的和； 若進行模擬，則每次query操作的最壞的時間復雜度為O(n)，在n較大時速度較慢。用前綴和也不能提高效率（每次add操作最壞為O(n)）。有一種數據結構，可以在O(n)時間裡初始化，用O(logn)的速度執行add操作或查詢前綴和，從而執行query操作。 首先，我們來介紹“lowbit”。對於一個數x，lowbit(x)是x的二進制裡最右面的1所代表的數字，例如lowbit(20)=4,因為20的二進制為10100，最右面的1代表4。怎樣計算lowbit呢？很簡單，lowbit(x)=x&-x。這是因為負數是用補碼保存的，-x就相當於(~x)+1。例（用8位計算）：  20=(00010100) -20=(11101100) 現在我們來介紹二叉索引樹。二叉索引樹在程序中也是用數組來保存的。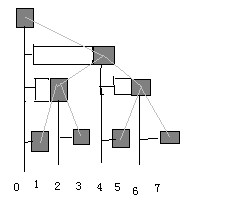 （畫得難看請見諒） 圖中，深灰色方塊代表樹中的結點（結點0為虛擬結點），灰色線段代表樹中的邊。這些邊並不需要顯式保存；對於一個節點x，若它是父結點的左子結點，則父結點編號為x-lowbit(x)，否則為x+lowbit(x)。圖中的每個結點左側都有一個白色長條（包括它自己），如結點4的長條為1~4，節點3的長條為3~3。不難發現，結點x的長條為(x-lowbit(x)+1)~x。 然後，我們用一個數組S儲存每個結點的白色長條內的所有數的和。例如，S4=A1+A2+A3+A4。這樣，就可以使用一個輔助的前綴和數組,在O(n)時間內從左到右初始化S數組。代碼如下：     1 int n; 2 int S[maxn],A[mxan],S1[maxn]; 3 int begin() 4 { 5 memset(S1,0,sizeof(S1)); 6 for(int i=1;i<=n;i++) 7 { 8 S1[i]=S1[i-1]+A[i]; 9 S[i]=S1[i]-S1[i-lowbit(i)]; 10 } 11 } View Code

 

最後讓我們來實現add操作和查詢操作。對於某個add操作的結點i，它的修改會影響到那些結點呢？很顯然，在它下面的結點（lowbit比它小）不會受到影響，在它左邊的結點也不會受到影響，所以只需要考慮在它右邊且lowbit比它大的第一個結點，這個結點的白色長條一定覆蓋x。很顯然，這個結點的編號為i+lowbit(i)。 接下來，x結點不需要考慮了，讓我們來考慮i+lowbit(i)結點。與上面一樣，只需要考慮在它右邊且lowbit比它大的第一個結點，所以只需要讓i+=lowbit(i)。代碼如下： 1 void add(int i,int x) 2 { 3 //若需要其他操作，可以加一句： 4 //A[i]+=x; 5 while(i<=n) 6 { 7 S[i]+=x;i+=lowbit(i); 8 } 9 } View Code

 

查詢前綴和的方法與之類似，只是i+=lowbit(i);改成了i-=lowbit(i);這裡不再介紹證明方法，與上面類似。代碼如下：

1 int query2(int i) 2 { 3 int sum=0; 4 while(i!=0) 5 { 6 sum+=S[i];i-=lowbit(i); 7 } 8 return sum; 9 } 10 int query(int l,int r) 11 { 12 return query2(r)-query2(l-1); 13 } View Code

 

 

最後，若有建議請提出。