並查集(UnionSet)是一種樹型的數據結構,用於處理一些不相交集合)的合並及查詢問題。常常在使用中以森林來表示。
並查集實現了將N個不同的元素分成一組不相交的集合。開始時,每個元素就是一個集合,然後按規律將兩個集合進行合並。
比如:現在有 0,1,2,3,4,5,6,7,8,9 總共10個元素。它們組成了3個集合,如圖:
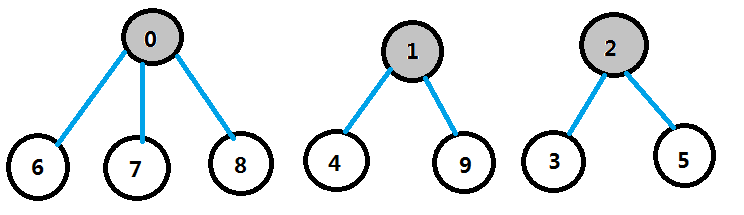
開始時,將每個元素都當做一個單元素的集合,並將每個元素都初始化為-1,如圖:

根據集合按規律將兩兩集合進行合並, 6、7、8屬於0這個集合,所以把6、7、8這三個位置都置0,而0這個位置減去3;1和2這兩個集合類似,4和9都屬於1這個集合,所以將4、9這兩個位置都置為1,並將位置1的數據減2;3、5同屬於集合2,所以將位置3、5的數據置為2,將位置2的數據減去2,即:

這樣我們可以根據負數的個數清晰的看出有幾個集合,並且我們也可以清晰的看出某節點是屬於哪個集合的。有3個負數,所以有3個集合,3、5位置數據為2,所以它們屬於集合2;6、7、8位置的數據都為0,所以它們都屬於集合0;4、9屬於集合集合1.
集合的合並:
形如:
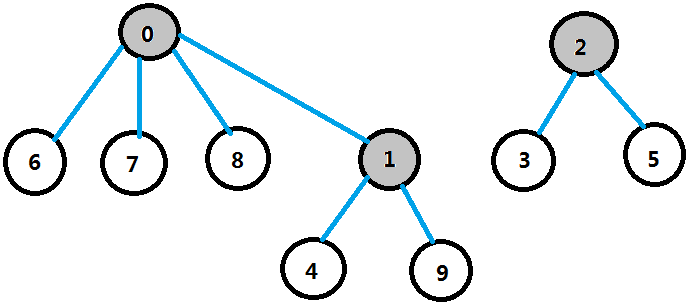
把集合1合並到集合0中,集合1有1、4、9三個元素,所以,將位置1設置為0,並將位置0的數據減去3,即:
由上圖我們可以看出4、9屬於集合1,集合1又屬於集合0;此時數組中共有2個負數,因此有兩個集合!
代碼實現:
class UnionSet
{
public:
UnionSet(size_t size)
:_size(size)
, _array(new int[size])
{
for (int i = 0; i < size; i++)
{ //將集合的每個元素都初始化為-1
_array[i] = -1;
}
}
//合並兩個集合
void Merge(int root1, int root2)
{
//找到root1所在集合的代表元素和root2所在集合的代表元素,鏈接
while (_array[root2] >= 0)
{
root2 = _array[root2];
}
while (_array[root1] >= 0)
{
root1 = _array[root1];
}
_array[root1] += _array[root2];
_array[root2] = root1;
}
//查找root對應集合的(根)代表元素
int Find(int root)
{
while (_array[root]>=0)
{
root = _array[root];
}
return root;
}
//打印
void Print()
{
for (int i = 0; i < _size; i++)
{
cout << _array[i] << " ";
}
cout << endl;
}
public:
int* _array;
size_t _size;
};
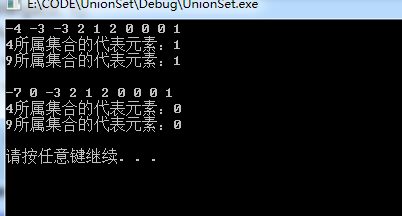
筆試題:
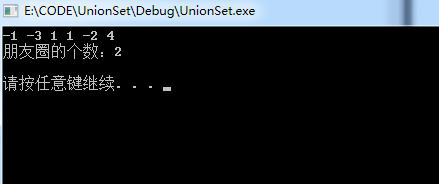
假如已知有n個人和m對好友關系(存於數組r),如果兩個人是直接的或間接的好友關系(好友的好友的好友....),則認為他們屬於同一好友圈,請求出這n個人中有幾個好友圈。
例如:n=5,m=3,r={{1,2},{2,3},{4,5}},表示有5個人,1和2是好友,2和3是好友,4和5是好友,則1.2.3屬於一個朋友圈,4.5屬於一個另朋友圈,結果為兩個朋友圈。
最後請分析所寫代碼的時間、空間復雜度。
這個題用利用並查集實現會比較簡易和高效!
需要建立一個函數來計算朋友圈的個數:
//計算朋友圈個數
int friends(int n, int m, int r[][2]) //n元素個數,m為每個朋友圈元素個數
{
UnionSet uf(n + 1);
//初始化朋友圈
for (int i =0 ; i <= m; i++)
{
int first = r[i][0];
int second = r[i][1];
uf.Merge(first, second);
}
uf.Print();
//計算朋友圈的個數
int count = 0;
for (int i = 1; i <= n; i++)
{
if (uf._array[i] < 0)
{
count++;
}
}
return count;
}
代碼地址: https://github.com/Lynn-zhang/Data-Structure/blob/master/UnionSet.cpp