NYOJ:題目860 又見01背包,nyoj860
題目鏈接:http://acm.nyist.net/JudgeOnline/problem.php?pid=860
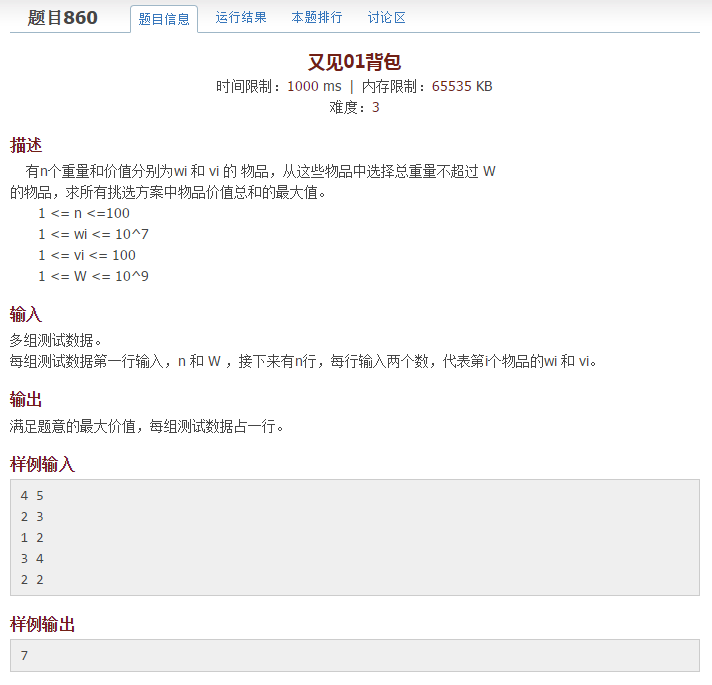
方法一:不用滾動數組(方法二為用滾動數組,為方法一的簡化)
動態規劃分析:最少要拿總價值一定,求所拿的最小質量(根據"最大能拿總重量一定,求能拿的最大價值"原理推導)
(PS:為了更好的理解,先不用滾動數組,直接開了兩個數組,第一個數組用來儲存最少要拿總價值為j時所拿的最小質量,第二個數組用來儲存第一個的改變前狀態)
例:
最大總質量sw = 5,物品數量n = 4;
1 2 3 4 <-第i個物品
w[] = {2, 1, 3, 2} //重量
v[] = {3, 2, 4, 2} //價值
最大總質量sw = 5,最大總價值sv = 11,物品數量n = 4;
分析打表結果如下:
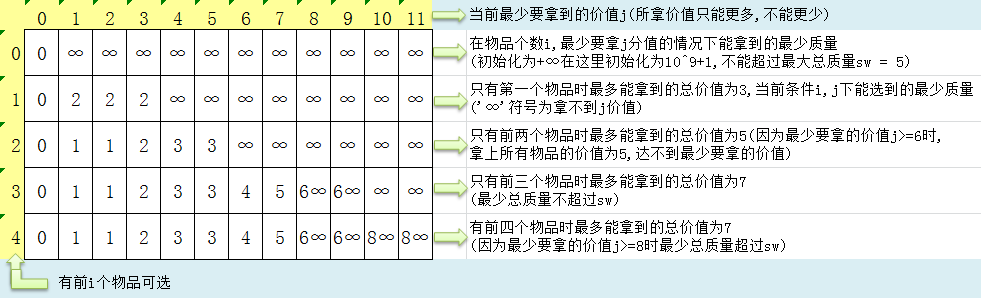

![]()
1 #include<iostream>
2 using namespace std;
3 int main() {
4 int n, sw, sv, v[105], w[105], m[10005], b[10005]; //n為物品數量,sw為總重量,sv為總價值
5 while(cin >> n >> sw) { //m[j]為最少要拿總價值為j時所拿的最小質量
6 sv = 0; //b[i]用來儲存m[i]的上一個狀態,如果用滾動數組方法就可以去掉b[]數組
7 for(int i = 1; i <= n; i++) {
8 cin >> w[i] >> v[i];
9 sv += v[i];
10 }
11 for(int j = 1; j <= 10000; j++) {
12 m[j] = 1000000001; //初始化為題目范圍內最大值
13 b[j] = m[j];
14 }
15 m[0] = b[0] = 0;
16 for(int i = 1; i <= n; i++) {
17 for(int j = 1; j <= sv; j++) {
18 if(j >= v[i]) m[j] = min(b[j], b[j-v[i]]+w[i]);
19 else m[j] = min(b[j], w[i]);
20 }
21 for(int j = 0; j <= sv; j++) {
22 b[j] = m[j];
23 //b[j] > 1000000000 ? cout << "+ " : cout << b[j] << " "; //去掉這兩行注釋可打表結果
24 }
25 //cout << endl;
26 }
27 int big = 1; //從價值為1開始找所有能拿到的價值
28 while(big <= sv && b[big] <= sw) big++;
29 cout << big-1 << endl;
30 }
31 }
代碼實現(點擊展開)
方法二:用滾動數組(方法一的簡化)
原理:利用方法一的表格,按照價值j倒序計算表中的值

![]()
1 #include<iostream>
2 using namespace std;
3 int main() {
4 int n, sw, sv, v[105], w[105], m[10005]; //n為物品數量,sw為總重量,sv為總價值
5 while(cin >> n >> sw) { //m[j]為最少要拿總價值為j時所拿的最小質量
6 sv = 0;
7 for(int i = 1; i <= n; i++) { cin >> w[i] >> v[i]; sv += v[i]; }
8 for(int j = 1; j <= 10000; j++) m[j] = 1000000001; //初始化為題目范圍內最大值
9 for(int i = 1; i <= n; i++) {
10 for(int j = sv; j >= 1; j--) {
11 if(j >= v[i]) m[j] = min(m[j], m[j-v[i]]+w[i]);
12 else m[j] = min(m[j], w[i]);
13 //m[j] > 1000000000 ? cout << "+ " : cout << m[j] << " "; //去掉這兩行注釋可打表結果
14 }
15 //cout << endl;
16 }
17 int big = 1; //從價值為1開始找所有能拿到的價值
18 while(big <= sv && m[big] <= sw) big++;
19 cout << big-1 << endl;
20 }
21 }
代碼實現(點擊展開)
開始寫於:2016.5.20 ----志銀



