上一篇文章中,算是初步了解了二叉樹是一種怎樣的數據結構,也算是有了一個初步的印象。接下來用自己的代碼去實現一個二叉搜索樹(以下全叫二叉樹)類,對外提供常用的接口,比如insert、erase、size、find等等。就像蓋房一樣,如果說二叉樹是一座建築,那麼其中的節點就是一塊塊磚。要實現二叉樹這個類,就必須先實現節點類,假設我們起名為treeNode。在STL標准庫中,像一般的數據結構都是模板類,在這裡為了方便起見,假設二叉樹這個類中保存的數據全是int型。
這個節點類中,需要包含如下的一些成員:節點值value,指向左子節點的指針left,指向右子節點的指針right,指向父節點的指針parent。用代碼實現如下:
class treeNode
{
public:
int value;
treeNode *left;
treeNode *right;
treeNode *parent;
treeNode()
{
value = 0;
left = NULL;
right = NULL;
parent = NULL;
}
};
為了方便起見,我們將值初始化為0,指針全部初始化為NULL。
有了這個類以後,等於有了蓋房子的基本原料。現在還需要實現二叉樹類,目的就是按照一定的規則,將一個個節點添加進來,構成二叉樹。與此同時還需要向外部用戶提供友好的接口,而不必關心內部的細節。比如說,我現在想將值為12的一個節點插入二叉樹,只需要調用insert(12)即可,而不是先生成一個節點的實例,賦值為12,再調整指針,插入二叉樹,同時還要保證二叉樹的結構特性。這些實現細節都需要用insert函數封裝起來。
在二叉樹這個類中,需要包含如下的成員,insert()、erase()、find()、size()成員函數,treeSize,根節點的指針root。當然還有一個構造函數。用代碼實現如下:
class searchTree
{
public:
searchTree(const int &value);
int insert(const int &value);
int erase(const int &value);
treeNode* find(const int &value);
int size() const;
private:
int treeSize;
treeNode* root;
};
在構造函數中,我們將二叉樹的實例初始化為包含一個根節點,根節點值為value的樹。
insert函數首先會生成一個節點實例,節點值為value,然後將這個節點插入到樹中。插入成功返回0,插入失敗返回非0,當樹中包含有相同的節點,即已經存在值為value的節點,插入失敗。
erase函數刪除樹中一個值為value的節點,刪除成功返回0,刪除失敗返回非0,當樹中不包含值為value的節點,刪除失敗。
find函數會在樹中查找值為value的節點,返回該節點的指針。如果查找成功返回該節點的指針,查找失敗返回NULL,如果樹中不包含值為value的節點,查找失敗。
size函數返回當前樹中節點的數量。
私有成員變量treeSize保存當前樹中節點的個數,指針root保存跟節點的地址。
接下來實現構造函數,構造函數中只需要生成一個根節點的實例,然後將根節點的值設為value,同時treeSize值為1,表示當前樹中有一個節點。代碼如下:
searchTree::searchTree(const int &value)
{
root = new treeNode();
root->value = value;
treeSize = 1;
}
接下來實現size函數,因為size函數最簡單,直接返回當前樹中節點的個數。代碼如下:
int searchTree::size()
{
return treeSize;
}
接下來實現find函數,find函數會在樹中查找值為value的節點,返回這個節點的指針。實現的思路就是從根節點開始比較根節點值和value的大小關系,如果根節點的值大於value,就沿左子節點下降,否則就沿右子節點下降。遵循這種下降規則,會出現兩種可能,第一種就是找到節點值和value相等的節點,返回節點指針。第二種就是下降到一個空節點,也就是NULL,此時返回NULL,代表查找失敗。代碼如下:
treeNode* searchTree::find(const int &value)
{
treeNode *curr;
curr = root; //從根節點開始從上到下查找
while (curr!=NULL) //終止條件之一就是下降到空節點
{
if ((curr->value) > value) //值小於當前節點的值,沿左子節點下降
{
curr = curr->left;
}
else if ((curr->value)right;
}
else //值等於當前節點的值,查找結束,返回
{
return curr;
}
}
return NULL; //已經下降到空節點還是沒找到該節點,代表該節點不在樹中,查找失敗,返回NULL
}
接下來實現insert函數,insert函數會在當前的樹中插入一個節點值為value的節點。函數的實現思想和find函數是類似的,也是從根節點開始比較根節點的值和value的大小關系,如果根節點值大於value,就沿左子節點下降,否則沿右子節點下降。這樣下降最終會出現兩種可能,第一種就是找到一個節點值和value大小相等,此時代表樹中已經有值為value的節點,返回1,代表插入失敗。第二種就是下降到一個空節點,也就是NULL,此時找到了正確的插入位置,新生成一個節點,賦值為value,插入到該位置。需要注意的問題就是在下降的過程中需要記錄當前節點的父節點,這樣當最終插入成功時,新生成的節點才知道自己的父節點是誰。還要記錄最後一次下降是沿左子節點還是右子節點下降,這樣最終插入的節點就知道自己是其父節點的左子節點還是右子節點。代碼如下:
int searchTree::insert(const int &value)
{
int direct = -1; //從上到下下降時,需要記錄上一次下降時沿左子節點還是沿右子節點下降
treeNode *curr,*par; //當前節點以及當前節點的父節點
curr = root; //從根節點開始從上到下查找
/*從上到下查找插入位置的過程需要保存當前節點的父節點,雖然每一個節點保存了自己的父節點,
但是插入的位置是一個空節點,也就是NULL,空節點是沒有自己的父節點*/
par = root;
while (curr!=NULL) //終止條件之一就是查找到一個空節點作為插入位置
{
par = curr; //保存父節點
if ((curr->value) > value) //如果值小於當前節點的值,沿左子節點下降
{
curr = curr->left;
direct = 0;
}
else if ((curr->value)right;
direct = 1;
}
else
{
return 1; //如果值等於當前節點的值,插入失敗,代表樹中已有該節點,返回1
}
}
curr = new treeNode(); //動態生成一個節點,賦值為value
curr->value = value;
if (direct!=-1) //如果值為-1,代表根節點為NULL,出現錯誤
{
if (direct == 0) //表示做後一次下降是沿左子節點下降,那麼新插入的節點就是父節點的左子節點
{
par->left = curr;
}
else //表示最後一次下降是沿右子節點下降,那麼新插入的節點就是父節點的右子節點
{
par->right = curr;
}
curr->parent = par; //更新插入節點的父節點
treeSize++; //節點數量加一
return 0;
}
return 1; //根節點為NULL,出現錯誤,返回1
}
接下來實現erase函數,這個函數放在最後一個就是因為這是最難的一個函數。我們的第一反應是刪除不是很簡單嗎,找到這個節點,釋放掉這段內存不就好了嗎。如果只是單純刪除一個節點,很簡單。難的地方在於刪除了這個節點之後,還要保持二叉樹的結構特性。也就是說刪除節點之後,剩下的結點還要組成一棵完整的樹,其中還有一層內在的含義就是,樹中的每個節點還要滿足左子節點值小於父節點,右子節點值大於父節點這樣的關系。
我們假設有下面這樣一棵樹:
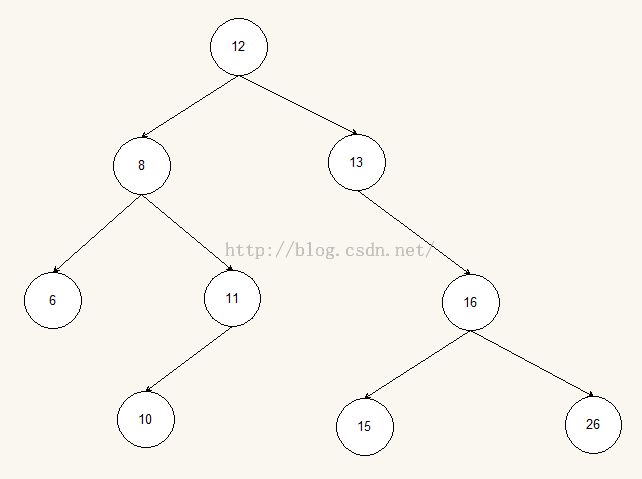
假設我們刪除8這個節點,如果按照上面的思想,只是單純的釋放掉8節點的內存,那麼根節點12就沒有了左子節點,左子節點指向了一段未分配的內存,這樣在訪問的時候就會出錯。如果不能沿左子節點下降,那麼剩下的6、11、10這三個節點都不能被訪問。產生的還有一個問題就是節點6、11沒有了自己的父節點,那麼在遍歷樹的時候,是不能沿父節點返回的。顯然這種刪除的方法是不科學的。可是如果刪除10節點,如果還按原先的思路,釋放10節點的內存,將11節點左子節點指針指向NULL,好像又是合理的。
節點8和節點10的區別就在於8的左右子節點均不為空,而10節點的左右子節點均為空。這樣我們就按左右子節點是否為空的原則,將節點分為四種情況:
1、左右子節點均為空。
2、左子節點為空,右子節點不為空。
3、右子節點為空,左子節點不為空。
4、左右子節點均不為空。
針對上述四種情況,我們要找出不同的刪除規則,目的都是一樣的。那就是找出一個替代節點,替代當前被刪除的節點,這個替代節點的作用就是替代掉被刪除的節點,依然能保證剩余的節點依然是一棵完整的二叉樹。
第一種情況下,替代節點就是NULL。
第二種情況下,上圖中13節點滿足這種情況,此時找到的替代節點就是它的右子節點,16節點。
第三種情況下,上圖中的11節點滿足這種情況,此時找到的替代節點就是它的左子節點,10節點。
第四種情況下,上圖中的8節點滿足這種情況,此時找替代節點的方法就是先下降到該節點的右子節點,也就是11節點。,如果該節點沒有左子節點,那麼該節點就是替代節點,也就是圖中的11節點。如果有左子節點,就再沿該節點的左子節點一直下降到末端。此時找到的替代節點就是圖中的10節點。
替代節點並不是唯一的,只要找到的替代節點能保證剩余的節點依然是一棵完整的二叉樹即可。尋找的過程中,要保持一個固定的規則不變,而且要盡量簡單、快速。上述尋找的過程中我們的規則就是先將節點分類,再針對四種不同的情況,設置四種子規則。代碼如下:
int searchTree::erase(const int &value)
{
treeNode *curr, *par, *replace, *replacePar; //分別為當前節點,當前節點的父節點,替代節點,替代節點的父節點
int direct = -1;
curr = root; //從根節點開始查找待刪除的點,查找過程和find函數一致
par = root;
while (curr!=NULL)
{
if ((curr->value) > value)
{
par = curr;
curr = curr->left;
direct = 0;
}
else if ((curr->value)right;
direct = 1;
}
else //找到了待刪除的點
{
if (curr->left==NULL&curr->right==NULL) //對應於情況1,左右子節點均為NULL,也就是該節點為葉節點
{
if (direct == 0) //根據最後一次下降方向,將父節點的左子節點或右子節點置為NULL
{
par->left = NULL;
}
else if (direct==1)
{
par->right = NULL;
}
delete curr; //釋放內存,節點數量減一
treeSize--;
return 0;
}
else if (curr->left==NULL&curr->right!=NULL) //對應於情況2,左子節點為空,右子節點不為空
{
replace = curr->right; //替代節點就是當前節點的右子節點
/*根據最後一次下降方向,將父節點的左子節點或者右子節點置為替代節點,替代節點父節點為當前節點的父節點*/
if (direct == 0)
{
par->left = replace;
replace->parent = par;
}
else if (direct==1)
{
par->right = replace;
replace->parent = par;
}
else //direct=-1表示刪除的根節點,將根節點設置為替代節點,替代節點的父節點置為NULL
{
root = replace;
replace->parent = NULL;
}
delete curr; //釋放當前節點的內存,節點數量減一
treeSize--;
return 0;
}
else if (curr->left != NULL&curr->right == NULL) //對應於情況3,和情況2類似
{
replace = curr->left;
if (direct == 0)
{
par->left = replace;
replace->parent = par;
}
else if (direct == 1)
{
par->right = replace;
replace->parent = par;
}
else
{
root = replace;
replace->parent = NULL;
}
delete curr;
treeSize--;
return 0;
}
else //左右節點均不為空
{
replace = curr->right; //先將替代節點暫定為當前節點右子節點
if (replace->left==NULL) //如果右子節點的左子節點為NULL,那麼右子節點就是替代節點
{
replace->left = curr->left; //更新替代節點的左子節點為當前節點的左子節點
if (curr->left!=NULL)
{
/*如果當前節點的左子節點存在,更新左子節點的父節點。此時如果左子節點為NULL,NULL是沒有父節點的*/
curr->left->parent = replace;
}
}
else //右子節點左子節點不為NULL,此時就要沿著左子節點一直下降到末端
{
replacePar = replace; //下降的過程保存替代節點的父節點
while (replace->left != NULL) //一直下降到末端
{
replacePar = replace;
replace = replace->left;
}
/*下降到末端時,替代節點會出現兩種情況。第一種是替代節點的右子節點不為NULL,
那麼就需要將其右子節點作為替代節點父節點的左子節點,也就是將替代節點的右子樹,
重新鏈接在樹上*/
replacePar->left = replace->right; //無論哪種情況,都將替代節點的右子節點作為替代節點父節點的左子節點
if (replace->right!=NULL) //如果右子節點不為NULL,要更新右子節點的父節點
{
replace->right->parent = replacePar;
}
replace->left = curr->left; //更新替代節點的左子節點指針
curr->left->parent = replace;
replace->right = curr->right; //更新替代節點的右子節點指針
curr->right->parent = replace;
}
if (direct == 0) //根據最後一次下降方向,再更新父節點的指針
{
par->left = replace;
replace->parent = par;
}
else if (direct == 1)
{
par->right = replace;
replace->parent = par;
}
else
{
root = replace;
replace->parent = NULL;
}
delete curr; //釋放掉當前節點的內存,樹中節點數量減一
treeSize--;
return 0;
}
}
}
return 1;
}
刪除一個節點難就難在最後一種情況,根據下圖說明一下如何刪除一個左右子節點均不為空的情況
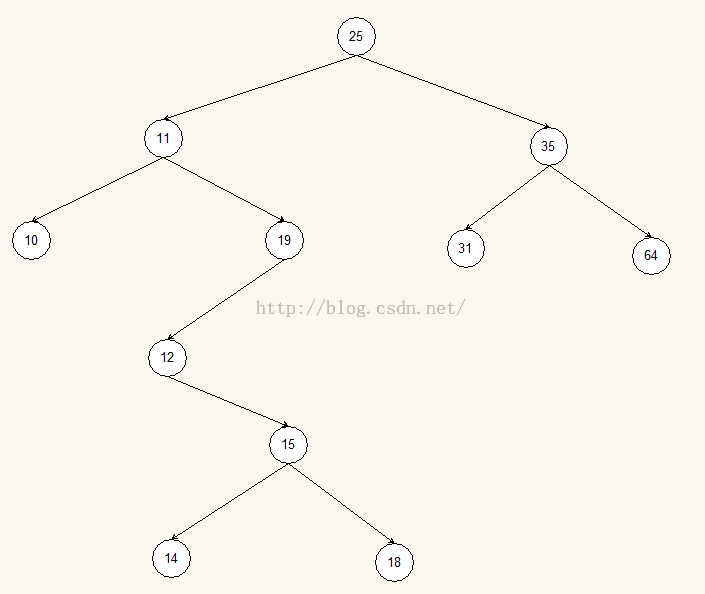
現在假設刪除節點36和節點11。
刪除節點35:首先找到節點35的右子節點,節點64,發現64的左子節點為NULL,那麼64就是替代節點。此時刪除掉35節點需要更新有關35節點的三個關系指針,就是和左子節點的關系指針,和右子節點的關系指針,和父節點的關系指針。首先將節點64的左子節點指針設置為35的左子節點,也就是31節點,將31節點的父節點指針設置為節點64。左子節點關系指針更新完畢。同理再更新父節點的關系指針。因為替代節點就是刪除節點的右子節點,所以右子節點的關系指針不需要更新。
刪除節點11,首先將替代節點暫定為刪除節點的右子節點,發現右子節點的左子節點不為NULL,沿著左子節點一直下降到末端,也就是節點12,為替代節點。此時要同時更新左子節點,右子節點,父節點的關系指針(簡單的理解就是將節點12填充到原來11的位置,更新節點12與周邊的關系)。更新完以後,發現從節點15以下的全部節點脫離了原來的樹,所以還需要更新節點15與節點19的關系。
這等於說刪除節點11是按兩個步驟進行的,第一步找到替代節點,並從樹中刪除,因為此時替代節點是沿左子節點一直下降到末端,那麼其左子節點必為NULL,那麼刪除替代節點的操作等於情況1或者情況2。第二步再將替代節點填充到刪除節點的位置,更新與周邊的關系指針,釋放刪除節點的內存。
到此,我們為了測試方便,還需要拿到一棵樹的根節點,如果按照中序遍歷輸出樹中的全部節點,就會按照從小到大排序的順序輸出。拿到這個根節點有兩種方法,第一種就是將類中的root節點設置為public,或者我們還需要在類中再添加一個方法rootNode,返回當前的根節點。考慮到封裝,後者還是比較好。考慮到安全性,應該將返回的指針設置為常量,這裡為了方便。
treeNode* searchTree::rootNode()
{
return root;
}
為了測試,我們還需要一個按中序將樹中節點輸出的函數,為了代碼簡潔,采用遞歸的方式。代碼如下:
void output(treeNode *node)
{
if (node!=NULL)
{
output(node->left);
cout << node->value << "-";
output(node->right);
}
}
到此為止,准備工作全部結束,寫一個簡單的測試函數,測試一下我們自己實現的二叉樹。代碼如下:
int main()
{
treeNode *root,*curr;
searchTree tree(100);
for (size_t i = 0; i < 20; i++)
{
tree.insert(rand() % 200);
}
cout << tree.size() << endl;
curr = tree.find(41);
if (curr!=NULL)
{
cout << "find the node" << endl;
}
else
{
cout << "the node is not in the tree" << endl;
}
tree.erase(41);
root = tree.rootNode();
output(root);
}
首先聲明一個樹的實例,根節點為100,再隨機生成20個0-199的數插入到樹中。然後查找值為41的節點,最後將這個節點刪除。最後打印樹中全部節點,如果節點是按從小到大順序打印,就代表這是一棵完整的二叉樹。輸出結果如下:
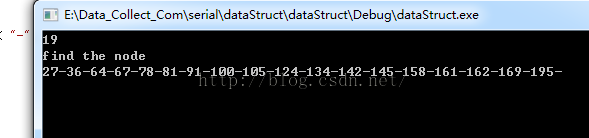
剛開始size為19的原因是隨機可能生成重復點,這樣插入就會失敗。我們看到節點以及從小到大順序打印。最後再上傳一張在vs環境下,樹的內存分布圖: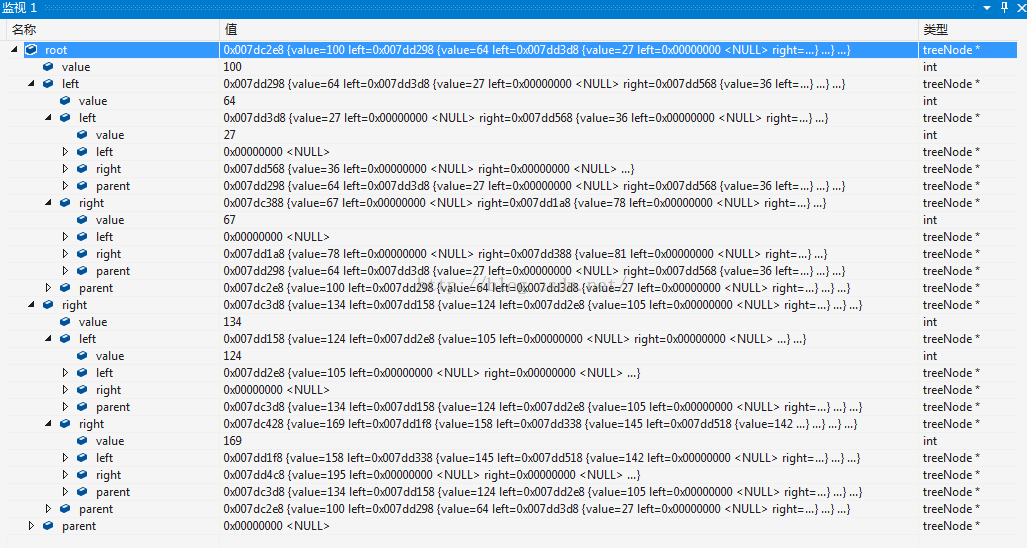
我們可以清晰地看到根節點為100,左右子節點分別為64和134。節點64的左右子節點分別為27和67,也可以清晰地看到它們在內存中的分布情況。