對稱矩陣及對稱矩陣的壓縮存儲，矩陣

對稱矩陣及對稱矩陣的壓縮存儲，矩陣

設一個N*N的方陣A，A中任意元素A[i][j]，當且僅當A[i][j] == A[j][i](0 <= i <= N-1 && 0 <= j <= N-1)，則矩陣A是對稱矩陣。

以矩陣的對角線為分隔，分為上三角和下三角。

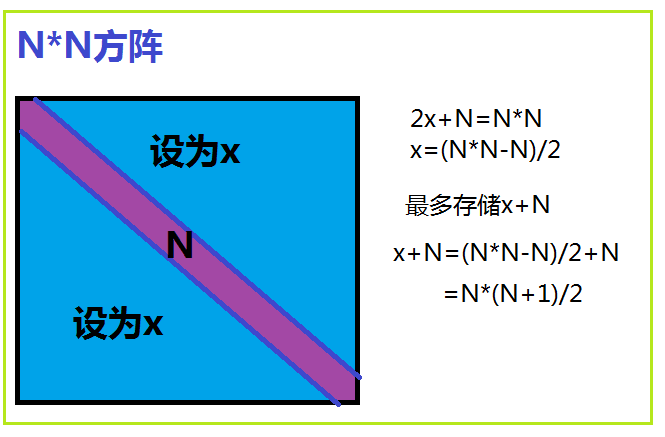
如上圖，對稱矩陣壓縮存儲存儲時只需要存儲上三角/下三角的數據，一般情況下用下三角存儲，所以最多存儲n(n+1)/2個數據。

對稱矩陣和壓縮存儲的對應關系：

下三角存儲i>=j,  SymmetricMatrix[i][j] == Array[i*(i+1)/2+j]

template<class T>
class SymmetricMatrix
{
public:
    SymmetricMatrix(T* array, size_t n)
    {
        _arraySize = n*(n + 1) / 2;
        _size = n;
        _array = new T[_arraySize];
        assert(array);
        for (size_t i = 0; i < n; i++)
        {
            for (size_t j = 0; j < n; j++)
            {
                _array[i*(i + 1) / 2 + j] = array[i*n + j];
            }
        }
    }
    T& GetPos(size_t row, size_t col)    // 獲取節點
    {
          //如果該位置為上三角的，利用對稱原理，交換該位置的行和列即可
        if (row < col)   
        {
            swap(row, col);
        }
        return _array[row*(row + 1) / 2 + col];
    } 
    void Display()     //打印
    {
        for (int i = 0; i < _size; i++)
        {
            for (int j = 0; j < _size; j++)
            {
                if (i >= j)
                {
                    cout << _array[i*(i + 1) / 2 + j] << " ";
                }
                else if (i<j)
                {
                    cout << _array[j*(j + 1) / 2 + i] << " ";
                }
            }
            cout << endl;
        }
        cout << endl;
    }
private:
    T *_array;      //壓縮矩陣
    size_t _size;   //方陣大小_size*_size
    size_t _arraySize;   //壓縮矩陣的總大小
};