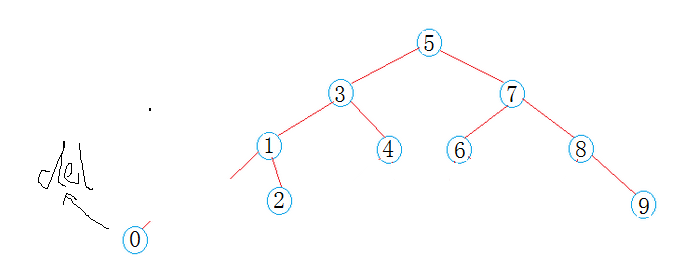
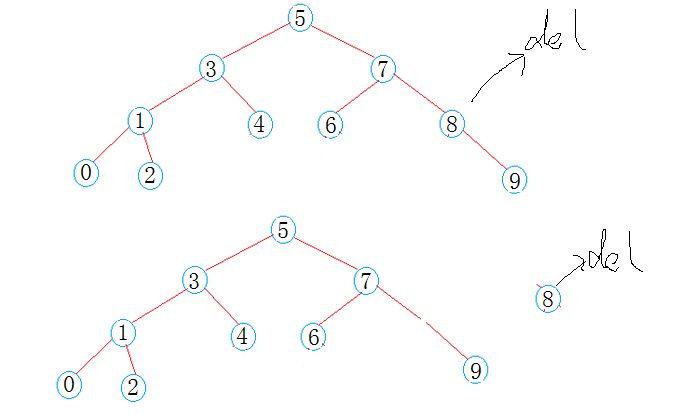
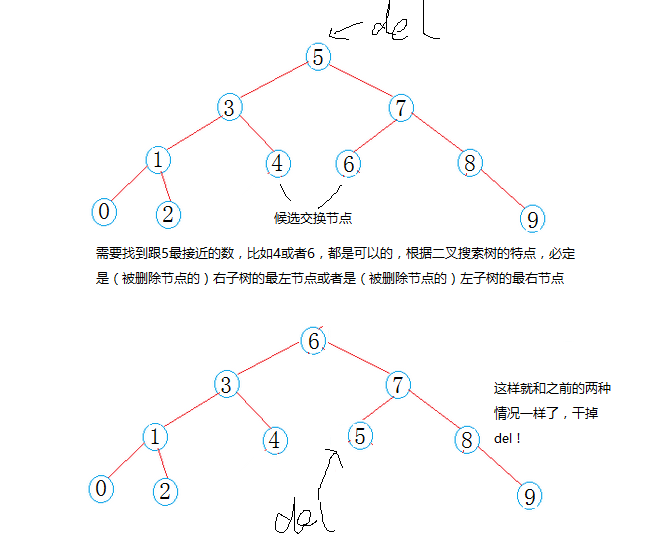
這次貼上二叉搜索樹的實現,搜索插入刪除我都實現了遞歸和非遞歸兩種版本(遞歸函數後面有_R標識)
1 #pragma once 2 #include<iostream> 3 using namespace std; 4 5 6 template<class K,class V> 7 struct BSTNode 8 { 9 K _key; 10 V _value; 11 BSTNode *_left; 12 BSTNode *_right; 13 BSTNode(const K& key, const V& value) 14 :_key(key) 15 ,_value(value) 16 ,_left(NULL) 17 ,_right(NULL) 18 { 19 } 20 }; 21 22 23 24 25 26 27 template<class K,class V> 28 class BSTree 29 { 30 typedef BSTNode<K, V> Node; 31 public: 32 BSTree() 33 :_root(NULL) 34 { 35 36 } 37 ~BSTree() 38 {} 39 bool Insert(const K& key,const V& value) 40 { 41 if (_root == NULL) 42 { 43 _root = new Node(key, value); 44 } 45 Node *cur = _root; 46 Node *parent = _root; 47 while (cur) 48 { 49 parent = cur; 50 if (cur->_key > key) 51 { 52 cur = cur->_left; 53 } 54 else if (cur->_key < key) 55 { 56 cur = cur->_right; 57 } 58 else 59 { 60 return false; 61 } 62 } 63 if (parent->_key > key) 64 { 65 parent->_left = new Node(key, value); 66 } 67 else 68 { 69 parent->_right = new Node(key, value); 70 } 71 return true; 72 } 73 bool Insert_R(const K& key, const V& value) 74 { 75 return _Insert_R(_root,key,value); 76 } 77 bool Remove(const K& key) 78 { 79 if (_root == NULL) 80 { 81 return false; 82 } 83 if (_root->_left == NULL && _root->_right == NULL) 84 { 85 delete _root; 86 _root = NULL; 87 return true; 88 } 89 Node *del = _root; 90 Node *parent = _root; 91 while (del && del->_key != key) 92 { 93 parent = del; 94 if (del->_key > key) 95 { 96 del = del->_left; 97 } 98 else if (del->_key < key) 99 { 100 del = del->_right; 101 } 102 } 103 if (del) 104 { 105 if (del->_left == NULL || del->_right == NULL) 106 { 107 if (del->_left == NULL) 108 { 109 if (parent->_left == del) 110 { 111 parent->_left = del->_right; 112 } 113 else 114 { 115 parent->_right = del->_right; 116 } 117 } 118 else 119 { 120 121 if (parent->_left == del) 122 { 123 parent->_left = del->_left; 124 } 125 else 126 { 127 parent->_right = del->_left; 128 } 129 } 130 delete del; 131 return true; 132 } 133 else 134 { 135 Node *InOrderfirst = del->_right; 136 Node *parent = del; 137 while (InOrderfirst->_left != NULL) 138 { 139 parent = InOrderfirst; 140 InOrderfirst = InOrderfirst->_left; 141 } 142 swap(del->_key, InOrderfirst->_key); 143 swap(del->_value, InOrderfirst->_value); 144 if (InOrderfirst->_left == NULL) 145 { 146 if (parent->_left == InOrderfirst) 147 { 148 parent->_left = InOrderfirst->_right; 149 } 150 else 151 { 152 parent->_right = InOrderfirst->_right; 153 } 154 } 155 else 156 { 157 158 if (parent->_left == InOrderfirst) 159 { 160 parent->_left = InOrderfirst->_left; 161 } 162 else 163 { 164 parent->_right = InOrderfirst->_left; 165 } 166 167 } 168 delete InOrderfirst; 169 return true; 170 } 171 } 172 return false; 173 } 174 bool Remove_R(const K& key) 175 { 176 return _Remove_R(_root, key); 177 } 178 Node *Find(const K& key) 179 { 180 Node *cur = _root; 181 while (cur) 182 { 183 if (cur->_key > key) 184 { 185 cur = cur->_left; 186 } 187 else if (cur->_key < key) 188 { 189 cur = cur->_right; 190 } 191 else 192 { 193 return cur; 194 } 195 } 196 return NULL; 197 } 198 Node *Find_R(const K& key) 199 { 200 return _Find_R(_root,key); 201 } 202 void InOrder() 203 { 204 return _InOrder(_root); 205 } 206 protected: 207 bool _Remove_R(Node *&root,const K& key) 208 { 209 if (root == NULL) 210 { 211 return false; 212 } 213 if (root->_key > key) 214 { 215 return _Remove_R(root->_left, key); 216 } 217 else if (root->_key < key) 218 { 219 return _Remove_R(root->_right, key); 220 } 221 else 222 { 223 if (root->_left == NULL || root->_right == NULL) 224 { 225 if (root->_left == NULL) 226 { 227 Node *del = root; 228 root = root->_right; 229 delete del; 230 return true; 231 } 232 else 233 { 234 Node *del = root; 235 root = root->_left; 236 delete del; 237 return true; 238 } 239 } 240 else 241 { 242 Node *InOrderfirst = root->_right; 243 while (InOrderfirst->_left != NULL) 244 { 245 InOrderfirst = InOrderfirst->_left; 246 } 247 swap(InOrderfirst->_key, root->_key); 248 swap(InOrderfirst->_value, root->_value); 249 return _Remove_R(root->_right, key); 250 } 251 } 252 } 253 void _InOrder(Node *root) 254 { 255 if (root == NULL) 256 { 257 return; 258 } 259 _InOrder(root->_left); 260 cout << root->_key << " "; 261 _InOrder(root->_right); 262 } 263 Node *_Find_R(Node *root, const K& key) 264 { 265 if (root == NULL) 266 { 267 return NULL; 268 } 269 if (root->_key < key) 270 { 271 return _Find_R(root->_right, key); 272 } 273 else if (root->_key > key) 274 { 275 return _Find_R(root->_left, key); 276 } 277 else 278 { 279 return root; 280 } 281 } 282 bool _Insert_R(Node *&root, const K& key, const V& value) 283 { 284 if (root == NULL) 285 { 286 root = new Node(key, value); 287 return true; 288 } 289 290 if (root->_key > key) 291 { 292 return _Insert_R(root->_left, key, value); 293 } 294 else if (root->_key < key) 295 { 296 return _Insert_R(root->_right, key, value); 297 } 298 else 299 { 300 return false; 301 } 302 } 303 protected: 304 Node *_root; 305 }; 306 307 308 void TestBinarySearchTree() 309 { 310 BSTree<int, int> bst1; 311 int a[10] = { 5,4,3,1,7,8,2,6,0,9 }; 312 for (int i = 0; i < 10; ++i) 313 { 314 bst1.Insert(a[i],a[i]); 315 } 316 // bst1.InOrder(); 317 //cout << endl; 318 //cout << bst1.Find(1)->_key << " "; 319 //cout << bst1.Find(5)->_key << " "; 320 //cout << bst1.Find(9)->_key << " "; 321 //cout << bst1.Find_R(1)->_key << " "; 322 //cout << bst1.Find_R(5)->_key << " "; 323 //cout << bst1.Find_R(9)->_key << " "; 324 //cout << endl; 325 bst1.Remove_R(5); 326 bst1.Remove_R(2); 327 bst1.Remove_R(8); 328 for (int i = 0; i < 10; ++i) 329 { 330 bst1.Remove_R(a[i]); 331 } 332 bst1.InOrder(); 333 bst1.Remove(5); 334 bst1.Remove(2); 335 bst1.Remove(8); 336 for (int i = 0; i < 10; ++i) 337 { 338 bst1.Remove(a[i]); 339 } 340 bst1.InOrder(); 341 }
二叉搜索樹的性質: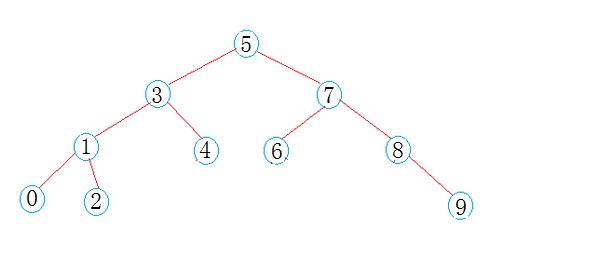
插入步驟很簡單,就是從根節點開始,進行比較,然後我那個左(右)子樹走,走到葉子節點之後,鏈接上就可以了
尋找也是類似插入的,很簡單
刪除就要略微繁瑣一點有三種情況(其實直接就可以歸類為兩種)