1 void CountSort(int *a , size_t size)
2 {
3 int max = a[0], min = a[0];
4 for (int i =1; i < size; ++i)
5 {
6 if (max < a[i])
7 {
8 max = a[i];
9 }
10 if (min > a[i])
11 {
12 min = a[i];
13 }
14 }
15 int index = 0;
16 int *CountArray = new int[max - min + 1];
17 memset(CountArray, 0, sizeof(int)*(max - min + 1));
18 for (int i = 0; i < size; ++i)
19 {
20 CountArray[a[i] - min]++;
21 }
22 for (int i = 0; i < max - min + 1; ++i)
23 {
24 for (int j = 0; j < CountArray[i]; ++j)
25 {
26 a[index++] = i + min;
27 }
28 }
29 }
所謂的基數排序原理就和哈希表極像,適合使用在待排序的數都處在一個比較小的范圍內,開辟好一定的輔助空間,按照直接定址法,將輔助空間對應的位置的計數增加,最後排序的時候只要把之前建好的輔助數組遍歷輸出一遍就好了
1 int GetMaxDigit(int *a,size_t size)
2 {
3 int digit = 1;
4 int max = 10;
5 for (int i = 0; i < size; ++i)
6 {
7 while (a[i] >= max)
8 {
9 digit++;
10 max *= 10;
11 }
12 }
13 return digit;
14 }
15
16 //一共需要幾個數組呢?一個count,一個start還有一個收集用的暫存數組?最後拷貝回去就可以了!
17 void DigitSort(int *a, size_t size)
18 {
19 int MaxDigit = GetMaxDigit(a, size);
20 int curDigit = 1;
21 int digit = 0;
22 int Count[10];
23 int Start[10];
24 int *Bucket = new int[size];
25 while (digit < MaxDigit)
26 {
27 memset(Count, 0, sizeof(int) * 10);
28 memset(Start, 0, sizeof(int) * 10);
29 for (int i = 0; i < size; ++i)
30 {
31 int num = a[i] / curDigit % 10;
32 Count[num]++;
33 }
34 Start[0] = 0;
35 for (int i = 1; i < 10; ++i)
36 {
37 Start[i] = Start[i - 1] + Count[i - 1];
38 }
39 for (int i = 0; i < size; ++i)
40 {
41 int num = a[i] / curDigit % 10;
42 Bucket[Start[num]++] = a[i];
43 }
44 memcpy(a, Bucket, sizeof(int)*size);
45 digit++;
46 curDigit *= 10;
47 }
48 }
基數排序又被稱為桶排序,這裡的代碼例子是完成一個幾位數的排序,可以看成先根據個位的數大小進行一次排序(扔進各自數的桶裡(桶當然是有序的(0-9嘛)))然後進行按序收集,然後根據十位數扔進桶裡,直到最高位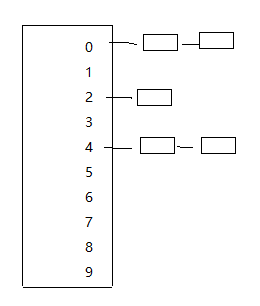
這裡我並未使用類似的鏈表結構,而是采用一個順序表
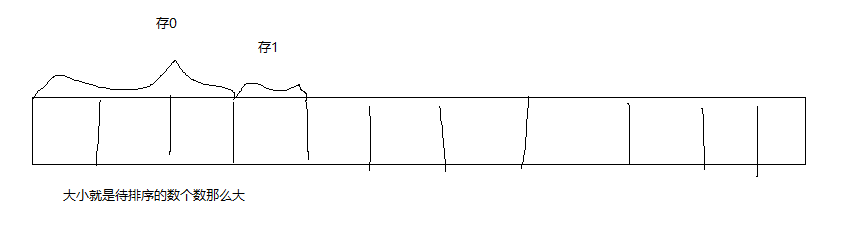
不停地往後存,使用count輔助數組進行計數(對應的0-9有幾個數),使用start數組計算每個待排序的數在上圖數組中的位置,上圖的數組就相當於收集了