談到鏈表之前,先說一下線性表。線性表是最基本、最簡單、也是最常用的一種數據結構。線性表中數據元素之間的關系是一對一的關系,即除了第一個和最後一個數據元素之外,其它數據元素都是首尾相接的。線性表有兩種存儲方式,一種是順序存儲結構,另一種是鏈式存儲結構。
順序存儲結構就是兩個相鄰的元素在內存中也是相鄰的。這種存儲方式的優點是查詢的時間復雜度為O(1),通過首地址和偏移量就可以直接訪問到某 元素,關於查找的適配算法很多,最快可以達到O(logn)。缺點是插入和刪除的時間復雜度最壞能達到O(n),如果你在第一個位置插入一個元素,你需要 把數組的每一個元素向後移動一位,如果你在第一個位置刪除一個元素,你需要把數組的每一個元素向前移動一位。還有一個缺點,就是當你不確定元素的數量時, 你開的數組必須保證能夠放下元素最大數量,遺憾的是如果實際數量比最大數量少很多時,你開的數組沒有用到的內存就只能浪費掉了。
我們常用的數組就是一種典型的順序存儲結構,如圖1。
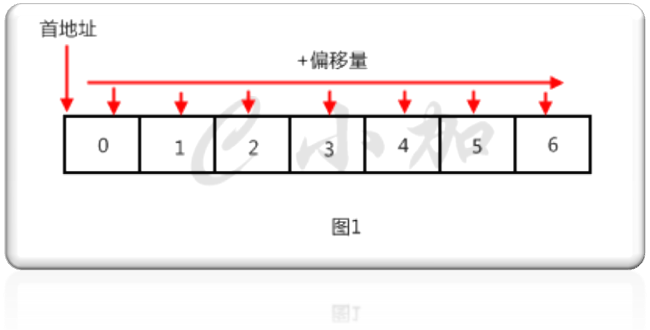
鏈式存儲結構就是兩個相鄰的元素在內存中可能不是相鄰的,每一個元素都有一個指針域,指針域一般是存儲著到下一個元素的指針。這種存儲方式的優點是 插入和刪除的時間復雜度為O(1),不會浪費太多內存,添加元素的時候才會申請內存,刪除元素會釋放內存,。缺點是訪問的時間復雜度最壞為O(n),關於 查找的算法很少,一般只能遍歷,這樣時間復雜度也是線性(O(n))的了,頻繁的申請和釋放內存也會消耗時間。
順序表的特性是隨機讀取,也就是訪問一個元素的時間復雜度是O(1),鏈式表的特性是插入和刪除的時間復雜度為O(1)。要根據實際情況去選取適合自己的存儲結構。
鏈表就是鏈式存儲的線性表。根據指針域的不同,鏈表分為單向鏈表、雙向鏈表、循環鏈表等等。
一、 單向鏈表(slist)
鏈表中最簡單的一種是單向鏈表,每個元素包含兩個域,值域和指針域,我們把這樣的元素稱之為節點。每個節點的指針域內有一個指針,指向下一個節點,而最後一個節點則指向一個空值。如圖2就是一個單向鏈表。
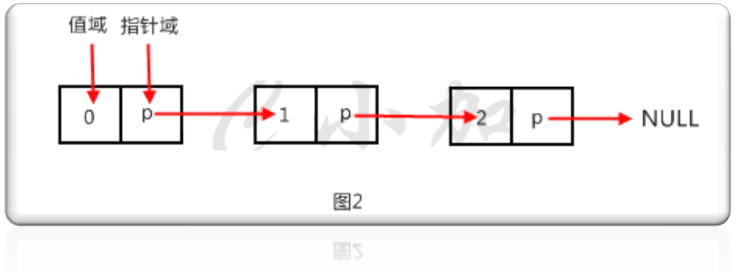
一個單向鏈表的節點被分成兩個部分。第一個部分保存或者顯示關於節點的信息,第二個部分存儲下一個節點的地址。單向鏈表只可向一個方向遍歷。
我寫了一個簡單的C++版單向鏈表類模板,就用這段代碼講解一下一個具體的單向鏈表該怎麼寫(代碼僅供學習),當然首先你要具備C++基礎知識和簡單的模板元編程。
完整代碼
首先我們要寫一個節點類,鏈表中的每一個節點就是一個節點類的對象。如圖3。
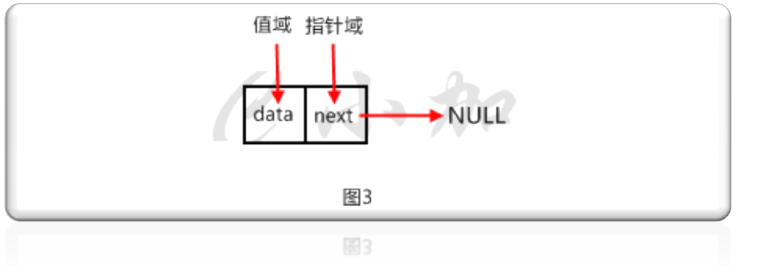
代碼如下:

template<class T>
class slistNode
{
public:
slistNode(){next=NULL;}//初始化
T data;//值
slistNode* next;//指向下一個節點的指針
};

第二步,寫單鏈表類的聲明,包括屬性和方法。
代碼如下:

template<class T>
class myslist
{
private:
unsigned int listlength;
slistNode<T>* node;//臨時節點
slistNode<T>* lastnode;//頭結點
slistNode<T>* headnode;//尾節點
public:
myslist();//初始化
unsigned int length();//鏈表元素的個數
void add(T x);//表尾添加元素
void traversal();//遍歷整個鏈表並打印
bool isEmpty();//判斷鏈表是否為空
slistNode<T>* find(T x);//查找第一個值為x的節點,返回節點的地址,找不到返回NULL
void Delete(T x);//刪除第一個值為x的節點
void insert(T x,slistNode<T>* p);//在p節點後插入值為x的節點
void insertHead(T x);//在鏈表的頭部插入節點
};

第三步,寫構造函數,初始化鏈表類的屬性。
代碼如下:

template<class T>
myslist<T>::myslist()
{
node=NULL;
lastnode=NULL;
headnode=NULL;
listlength=0;
}

第四步,實現add()方法。
代碼如下:

template<class T>
void myslist<T>::add(T x)
{
node=new slistNode<T>();//申請一個新的節點
node->data=x;//新節點賦值為x
if(lastnode==NULL)//如果沒有尾節點則鏈表為空,node既為頭結點,又是尾節點
{
headnode=node;
lastnode=node;
}
else//如果鏈表非空
{
lastnode->next=node;//node既為尾節點的下一個節點
lastnode=node;//node變成了尾節點,把尾節點賦值為node
}
++listlength;//元素個數+1
}

第五步,實現traversal()函數,遍歷並輸出節點信息。
代碼如下:

template<class T>
void myslist<T>::traversal()
{
node=headnode;//用臨時節點指向頭結點
while(node!=NULL)//遍歷鏈表並輸出
{
cout<<node->data<<ends;
node=node->next;
}
cout<<endl;
}

第六步,實現isEmpty()函數,判斷鏈表是否為空,返回真為空,假則不空。
代碼如下:
template<class T>
bool myslist<T>::isEmpty()
{
return listlength==0;
}
第七步,實現find()函數。
代碼如下:

template<class T>
slistNode<T>* myslist<T>::find(T x)
{
node=headnode;//用臨時節點指向頭結點
while(node!=NULL&&node->data!=x)//遍歷鏈表,遇到值相同的節點跳出
{
node=node->next;
}
return node;//返回找到的節點的地址,如果沒有找到則返回NULL
}

第八步,實現delete()函數,刪除第一個值為x的節點,如圖4。
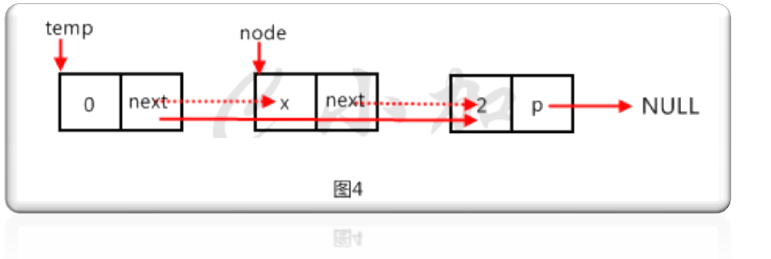
代碼如下:

template<class T>
void myslist<T>::Delete(T x)
{
slistNode<T>* temp=headnode;//申請一個臨時節點指向頭節點
if(temp==NULL) return;//如果頭節點為空,則該鏈表無元素,直接返回
if(temp->data==x)//如果頭節點的值為要刪除的值,則刪除投節點
{
headnode=temp->next;//把頭節點指向頭節點的下一個節點
if(temp->next==NULL) lastnode=NULL;//如果鏈表中只有一個節點,刪除之後就沒有節點了,把尾節點置為空
delete(temp);//刪除頭節點
return;
}
while(temp->next!=NULL&&temp->next->data!=x)//遍歷鏈表找到第一個值與x相等的節點,temp表示這個節點的上一個節點
{
temp=temp->next;
}
if(temp->next==NULL) return;//如果沒有找到則返回
if(temp->next==lastnode)//如果找到的時候尾節點
{
lastnode=temp;//把尾節點指向他的上一個節點
delete(temp->next);//刪除尾節點
temp->next=NULL;
}
else//如果不是尾節點,如圖4
{
node=temp->next;//用臨時節點node指向要刪除的節點
temp->next=node->next;//要刪除的節點的上一個節點指向要刪除節點的下一個節點
delete(node);//刪除節點
node=NULL;
}
}

第九步,實現insert()和insertHead()函數,在p節點後插入值為x的節點。如圖5。
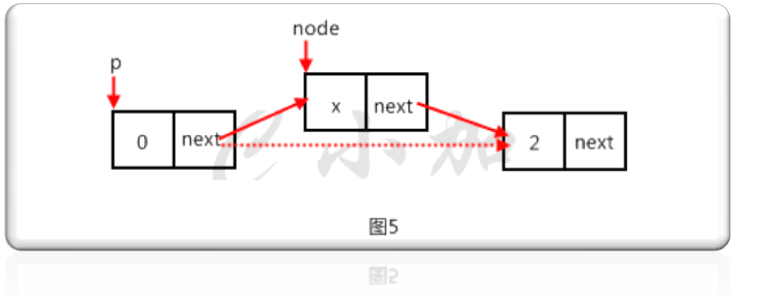
代碼如下:

template<class T>
void myslist<T>::insert(T x,slistNode<T>* p)
{
if(p==NULL) return;
node=new slistNode<T>();//申請一個新的空間
node->data=x;//如圖5
node->next=p->next;
p->next=node;
if(node->next==NULL)//如果node為尾節點
lastnode=node;
}
template<class T>
void myslist<T>::insertHead(T x)
{
node=new slistNode<T>();
node->data=x;
node->next=headnode;
headnode=node;
}

最終,我們完成一個簡單的單向鏈表。此單向鏈表代碼還有很多待完善的地方,以後會修改代碼並不定時更新。
二、 雙向鏈表
雙向鏈表的指針域有兩個指針,每個數據結點分別指向直接後繼和直接前驅。單向鏈表只能從表頭開始向後遍歷,而雙向鏈表不但可以從前向後遍歷,也可以 從後向前遍歷。除了雙向遍歷的優點,雙向鏈表的刪除的時間復雜度會降為O(1),因為直接通過目的指針就可以找到前驅節點,單向鏈表得從表頭開始遍歷尋找 前驅節點。缺點是每個節點多了一個指針的空間開銷。如圖6就是一個雙向鏈表。
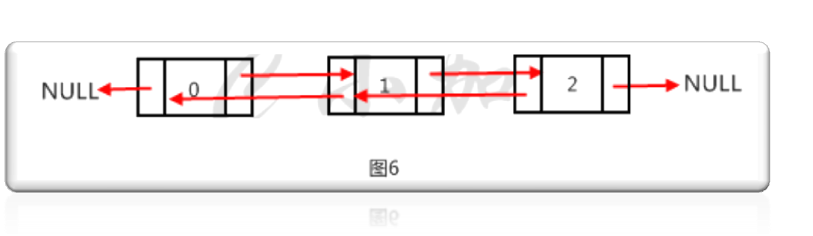
三、 循環鏈表
循環鏈表就是讓鏈表的最後一個節點指向第一個節點,這樣就形成了一個圓環,可以循環遍歷。單向循環鏈表可以單向循環遍歷,雙向循環鏈表的頭節點的指針也要指向最後一個節點,這樣的可以雙向循環遍歷。如圖7就是一個雙向循環鏈表。
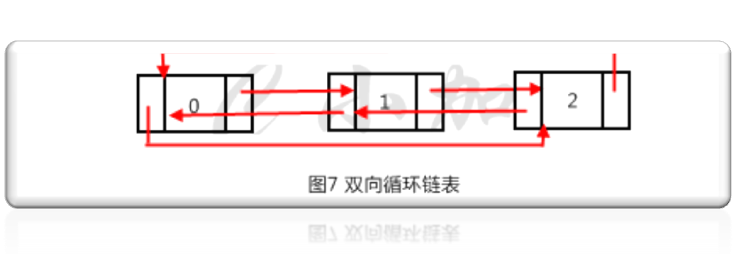
四、 鏈表相關問題
1、如何判斷一個單鏈表有環
2、如何判斷一個環的入口點在哪裡
3、如何知道環的長度
4、如何知道兩個單鏈表(無環)是否相交
5、如果兩個單鏈表(無環)相交,如何知道它們相交的第一個節點是什麼
6、如何知道兩個單鏈表(有環)是否相交
7、如果兩個單鏈表(有環)相交,如何知道它們相交的第一個節點是什麼
1、采用快慢步長法。
令兩個指針p和q分別指向頭結點,p每次前進一步,q每次前進兩步,如果p和q能重合,則有環。可以這麼理解,這種做法相當於p靜止不動,q每次前進一步,所有肯定有追上p的時候。
我們注意到,指針p和q分別以速度為1和2前進。如果以其它速度前進是否可以呢?
假設p和q分別以速度為v1和v2前進。如果有環,設指針p和q第一次進入環時,他們相對於環中第一個節點的偏移地址分別為a和b(可以把偏移地址理解為節點個數)
這樣,可以看出,鏈表有環的充要條件就是某一次循環時,指針p和q的值相等,就是它們相對環中首節點的偏移量相等。我們設環中的結點個數為n,程序循環了m次。
由此可以有下面等式成立:(mod(n)即對n取余)
(a+m*v1)mod(n) = (b+m*v2) mod(n)
設等式左邊mod(n)的最大整數為k1,等式右邊mod(n)的最大整數為k2,則
(a+m*v1)-k1*n = (b+m*v2)-k2*n
整理以上等式:
m= |((k2-k1)*n+a-b)/( v2-v1)| ①
如果是等式①成立,就要使循環次數m為一整數。顯然如果v2-v1為1,則等式成立。
這樣p和q分別以速度為v1和v2且|v2-v1|為1時,按以上算法就可找出鏈表中是否有環。當然|v2-v1|不為1時,也可能可以得出符合條件的m。

bool IsExitsLoop(slist *head)
{
slist *slow = head, *fast = head;
while ( fast && fast->next )
{
slow = slow->next;
fast = fast->next->next;
if ( slow == fast ) break;
}
return !(fast == NULL || fast->next == NULL);
}

時間復雜度分析:假設甩尾(在環外)長度為 len1(結點個數),環內長度為 len2,鏈表總長度為n,則n=len1+len2 。 當p步長為1,q步長為2時,p指針到達環入口需要len1時間,p到達入口後,q處於哪裡不確定,但是肯定在環內,此時p和q開始追趕,q最長需要 len2時間就能追上p(p和q都指向環入口),最短需要1步就能追上p(p指向環入口,q指向環入口的前一個節點)。事實上,每經過一步,q和p的距離 就拉近一步,因此,經過q和p的距離步就可以追上p。因此總時間復雜度為O(n),n為鏈表的總長度。
2、分別從鏈表頭和碰撞點,同步地一步一步前進掃描,直到碰撞,此碰撞點即是環的入口。
證明如下:
鏈表形狀類似數字 6 。
假設甩尾(在環外)長度為 a(結點個數),環內長度為 b 。
則總長度(也是總結點數)為 a+b 。
從頭開始,0 base 編號。
將第 i 步訪問的結點用 S(i) 表示。i = 0, 1 ...
當 i<a 時,S(i)=i ;
當 i≥a 時,S(i)=a+(i-a)%b 。
分析追趕過程。
兩個指針分別前進,假定經過 x 步後,碰撞。則有:S(x)=S(2x)
由環的周期性有:2x=tb+x 。得到 x=tb 。
另,碰撞時,必須在環內,不可能在甩尾段,有 x>=a 。
連接點為從起點走 a 步,即 S(a)。
S(a) = S(tb+a) = S(x+a)。
得到結論:從碰撞點 x 前進 a 步即為連接點。
根據假設易知 S(a-1) 在甩尾段,S(a) 在環上,而 S(x+a) 必然在環上。所以可以發生碰撞。
而,同為前進 a 步,同為連接點,所以必然發生碰撞。
綜上,從 x 點和從起點同步前進,第一個碰撞點就是連接點。

slist* FindLoopPort(slist *head)
{
slist *slow = head, *fast = head;
while ( fast && fast->next )
{
slow = slow->next;
fast = fast->next->next;
if ( slow == fast ) break;
}
if (fast == NULL || fast->next == NULL)
return NULL;
slow = head;
while (slow != fast)
{
slow = slow->next;
fast = fast->next;
}
return slow;
}

時間復雜度分析:假設甩尾(在環外)長度為 len1(結點個數),環內長度為 len2 。則時間復雜度為“環是否存在的時間復雜度”+O(len1)
3、從碰撞點開始,兩個指針p和q,q以一步步長前進,q以兩步步長前進,到下次碰撞所經過 的操作次數即是環的長度。這很好理解,比如兩個運動員A和B從起點開始跑步,A的速度是B的兩倍,當A跑玩一圈的時候,B剛好跑完兩圈,A和B又同時在起 點上。此時A跑的長度即相當於環的長度。
假設甩尾(在環外)長度為 len1(結點個數),環內長度為 len2 ,則時間復雜度為“環是否存在的時間復雜度”+O(len2)。
4、法一:將鏈表A的尾節點的next指針指向鏈表B的頭結點,從而構造了一個新鏈表。問題轉化為求這個新鏈表是否有環的問題。
時間復雜度為環是否存在的時間復雜度,即O(length(A)+length(B)),使用了兩個額外指針
法二:兩個鏈表相交,則從相交的節點起,其後的所有的節點都是都是兩個鏈表共有的。因此,如果它們相交,則最後一個節點一定是共有的。因此,判斷兩鏈表 相交的方法是:遍歷第一個鏈表,記住最後一個節點。然後遍歷第二個鏈表,到最後一個節點時和第一個鏈表的最後一個節點做比較,如果相同,則相交。
時間復雜度:O(length(A)+length(B)),但是只用了一個額外指針存儲最後一個節點
5、將鏈表A的尾節點的next指針指向鏈表B的頭結點,從而構造了一個環。問題轉化為求這個環的入口問題。
時間復雜度:求環入口的時間復雜度
6、分別判斷兩個鏈表A、B是否有環(注,兩個有環鏈表相交是指這個環屬於兩個鏈表共有)
如果僅有一個有環,則A、B不可能相交
如果兩個都有環,則求出A的環入口,判斷其是否在B鏈表上,如果在,則說明A、B相交。
時間復雜度:“環入口問題的時間復雜度”+O(length(B))
7、分別計算出兩個鏈表A、B的長度LA和LB(環的長度和環到入口點長度之和就是鏈表長度),參照問題3。
如果LA>LB,則鏈表A指針先走LA-LB,鏈表B指針再開始走,則兩個指針相遇的位置就是相交的第一個節點。
如果LB>LA,則鏈表B指針先走LB-LA,鏈表A指針再開始走,則兩個指針相遇的位置就是相交的第一個節點。
時間復雜度:O(max(LA,LB))