poj3070 Fibonacci

poj3070 Fibonacci

Description

In the Fibonacci integer sequence,F₀= 0,F₁= 1, andF_n=F_{n? 1}+F_{n? 2}forn≥ 2. For example, the first ten terms of the Fibonacci sequence are:

0, 1, 1, 2, 3, 5, 8, 13, 21, 34, …

An alternative formula for the Fibonacci sequence is

.

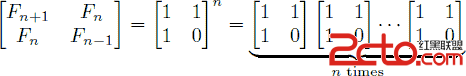Given an integern, your goal is to compute the last 4 digits ofF_n.

Input

The input test file will contain multiple test cases. Each test case consists of a single line containing n (where 0 ≤n≤ 1,000,000,000). The end-of-file is denoted by a single line containing the number ?1.

Output

For each test case, print the last four digits ofF_n. If the last four digits ofF_nare all zeros, print ‘0’; otherwise, omit any leading zeros (i.e., printF_nmod 10000).

Sample Input

0
9
999999999
1000000000
-1

Sample Output

0
34
626
6875

Hint

As a reminder, matrix multiplication is associative, and the product of two 2 × 2 matrices is given by

.

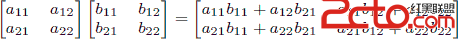Also, note that raising any 2 × 2 matrix to the 0th power gives the identity matrix:

.

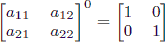Source

矩陣乘法裸題，題目已經把題解講的很清楚了...

#include
#include
#include
#include
#include
#include
#define F(i,j,n) for(int i=j;i<=n;i++)
#define D(i,j,n) for(int i=j;i>=n;i--)
#define ll long long
#define mod 10000
using namespace std;
int n;
struct matrix
{
	int f[2][2];
	matrix(){memset(f,0,sizeof(f));}
	friend matrix operator *(const matrix &a,const matrix &b)
	{
		matrix c;
		F(i,0,1) F(j,0,1) F(k,0,1) c.f[i][j]=(c.f[i][j]+a.f[i][k]*b.f[k][j])%mod;
		return c;
	}
};
int main()
{
	while (scanf("%d",&n))
	{
		if (n==-1) break;
		matrix a,b;
		a.f[0][0]=a.f[0][1]=a.f[1][0]=1;a.f[1][1]=0;
		b.f[1][0]=b.f[0][1]=0;b.f[0][0]=b.f[1][1]=1;
		for(;n;n>>=1,a=a*a) if (n&1) b=b*a;
		printf("%d\n",b.f[1][0]);
	}
	return 0;
}