選用合適的算法,求解三種線性方程組:一般線性方程組,對稱正定方程組,三對角線性方程組。
方程略。
Guass列主元是為了防止Guass消去法中大數吃掉小數而引出的一種線性方程組求解方法,消元時選用一列中絕對值最大的元素作為列主元素。
算法偽代碼:

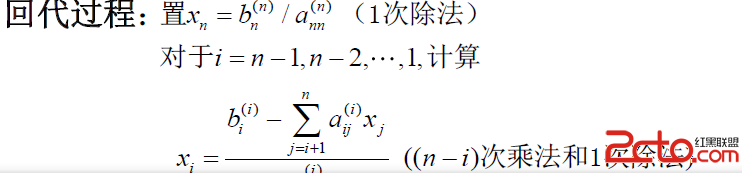
平方根法,它把系數矩陣(對稱正定矩陣)表示成一個下三角矩陣L和其轉置的乘積的分解。這種分解又稱為Cholesky分解。
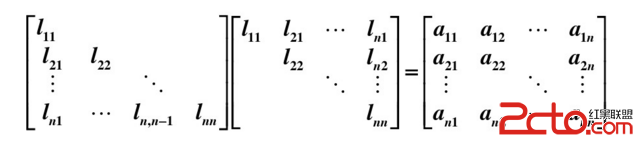
三對角線性方程組是指這一類的線性方程組:系數矩陣是一個對角占優的三對角矩陣。追趕法是專門用來求解三對角線性方程組的,它將系數矩陣分解成alpha矩陣和beta矩陣的乘積,如下圖所示:
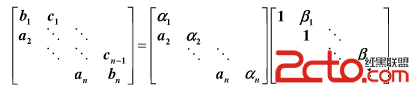
/*
CreateOn:2016/03/20
Author:linxiaobai
Function:linear equation solution
solution1:列主元Guass消去法求解一般線性方程組
*/
#include "stdafx.h"
# include
# include
# include
# include
# include
using namespace std;
double a[15][15];
const int N=10;
double res[N+1];
void printArry(double a[][15])//打印增廣矩陣
{
for(int i=1;i<=10;i++)
{
for(int j=1;j<=11;j++)
{
cout<
2,使用平方根算法解對稱正定方程組
/*
CreateOn:2016/03/20
Author:linxiaobai
Function:linear equation solution
solution1:使用平方根算法解對稱正定方程組
*/
# include"stdafx.h"
# include
# include
# include
# include
using namespace std;
double a[10][10];
const int N=8;
double b[N+1],xx[N+1],yy[N+1];
void printArry(double a[][10])//輸出系數矩陣
{
for(int i=1;i<=8;i++)
{
for(int j=1;j<=8;j++)
{
cout<=1;k--)
{
double s4=0;
for(int m=k+1;m<=N;m++)
s4+=a[m][k]*xx[m];
xx[k]=(yy[k]-s4)/a[k][k];
}
cout<
3,使用追趕法解三對角線性方程組
/*
CreateOn:2016/03/20
Author:linxiaobai
Function:linear equation solution
solution1:使用追趕法解三對角線性方程組
*/
# include"stdafx.h"
# include
# include
# include
# include
using namespace std;
const int N=10;
double a[N+1],c[N+1],d[N+1],xx[N+1],yy[N+1];
int main()
{
cout<<"【運用追趕法解三對角線性方程組】"<
四,數值結果1,Guass列主元消去法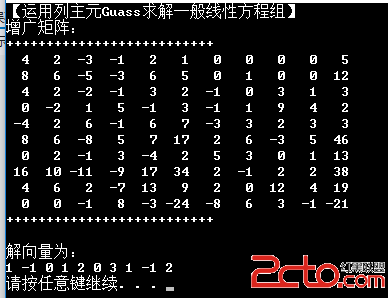
2,使用平方根算法解對稱正定方程組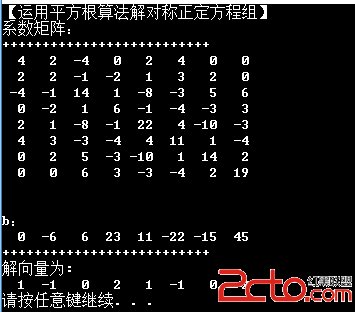
3,使用追趕法解三對角線性方程組
五,結果分析與實驗總結浮點計算產生的誤差在Guass消元算法之前的代碼中,我使用了近似的方法,將絕對值小於10的-14次方的值近似為0,現在去掉這個處理,來看一下結果:
for(int i=1;i<=N;i++)
//if(abs(res[i])<10e-14)
//cout<<"0"<<" ";
//else
cout<
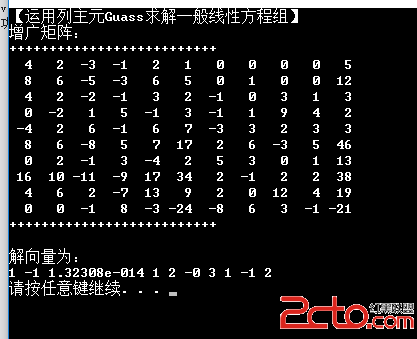
可以看到x3的值是一個十分接近於0的數,如果將消元後的系數矩陣打印出來,可以看到消元後的系數矩陣並不是一個真正的上三角矩陣,下三角部分有幾處的值是一個絕對值極小的值,這是由於計算機的浮點計算造成的,浮點數在計算機中本身就不是一個精確的數,在消元的過程中,一些浮點運算有誤差,於是最後得到的是近似值,而不是0。
同理,平方根法和追趕法也會產生由浮點數計算引起的誤差,減少計算誤差正是學習數值分析的目的。