Data Mining
1.多重共線性--預測變量之間相互關聯。多重共線性會導致解空間的不穩定,從而可能導致結果的不連貫。
2.高維空間本身具有稀疏性。一維正態分布有68%的值落於正負標准差之間,而在十維空間上只有0.02%。
3.過多的變量會妨礙查找規律的建立。
4.僅在變量層面上分析可能會忽略變量之間的潛在聯系。例如幾個預測變量可能落入僅反映數據某一方面特征的一個組內。
降維的目的:
1.減少預測變量的個數
2.確保這些變量是相互獨立的
3.提供一個框架來解釋結果
降維的方法有:主成分分析、因子分析、用戶自定義復合等。
PCA(Principal Component Analysis)不僅僅是對高維數據進行降維,更重要的是經過降維去除了噪聲,發現了數據中的模式。
PCA把原先的n個特征用數目更少的m個特征取代,新特征是舊特征的線性組合,這些線性組合最大化樣本方差,盡量使新的m個特征互不相關。從舊特征到新特征的映射捕獲數據中的固有變異性。
預備知識
樣本X和樣本Y的協方差(Covariance):
協方差為正時說明X和Y是正相關關系,協方差為負時X和Y是負相關關系,協方差為0時X和Y相互獨立。
Cov(X,X)就是X的方差(Variance).
當樣本是n維數據時,它們的協方差實際上是協方差矩陣(對稱方陣),方陣的邊長是。比如對於3維數據(x,y,z),計算它的協方差就是:
若,則稱
是A的特征值,X是對應的特征向量。實際上可以這樣理解:矩陣A作用在它的特征向量X上,僅僅使得X的長度發生了變化,縮放比例就是相應的特征值
。
當A是n階可逆矩陣時,A與P-1Ap相似,相似矩陣具有相同的特征值。
特別地,當A是對稱矩陣時,A的奇異值等於A的特征值,存在正交矩陣Q(Q-1=QT),使得:
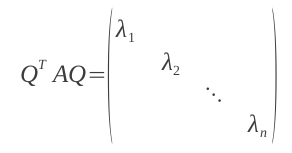
對A進行奇異值分解就能求出所有特征值和Q矩陣。
D是由特征值組成的對角矩陣
由特征值和特征向量的定義知,Q的列向量就是A的特征向量。
Jama包
Jama包是用於基本線性代數運算的java包,提供矩陣的cholesky分解、LUD分解、QR分解、奇異值分解,以及PCA中要用到的特征值分解,此外可以計算矩陣的乘除法、矩陣的范數和條件數、解線性方程組等。
PCA過程
1.特征中心化。即每一維的數據都減去該維的均值。這裡的“維”指的就是一個特征(或屬性),變換之後每一維的均值都變成了0。
很多數據挖掘的教材上都會講到鹫尾花的例子,本文就拿它來做計算。原始數據是150×4的矩陣A:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 1505.1 3.5 1.4 0.2
4.9 3.0 1.4 0.2
4.7 3.2 1.3 0.2
4.6 3.1 1.5 0.2
5.0 3.6 1.4 0.2
5.4 3.9 1.7 0.4
4.6 3.4 1.4 0.3
5.0 3.4 1.5 0.2
4.4 2.9 1.4 0.2
4.9 3.1 1.5 0.1
5.4 3.7 1.5 0.2
4.8 3.4 1.6 0.2
4.8 3.0 1.4 0.1
4.3 3.0 1.1 0.1
5.8 4.0 1.2 0.2
5.7 4.4 1.5 0.4
5.4 3.9 1.3 0.4
5.1 3.5 1.4 0.3
5.7 3.8 1.7 0.3
5.1 3.8 1.5 0.3
5.4 3.4 1.7 0.2
5.1 3.7 1.5 0.4
4.6 3.6 1.0 0.2
5.1 3.3 1.7 0.5
4.8 3.4 1.9 0.2
5.0 3.0 1.6 0.2
5.0 3.4 1.6 0.4
5.2 3.5 1.5 0.2
5.2 3.4 1.4 0.2
4.7 3.2 1.6 0.2
4.8 3.1 1.6 0.2
5.4 3.4 1.5 0.4
5.2 4.1 1.5 0.1
5.5 4.2 1.4 0.2
4.9 3.1 1.5 0.1
5.0 3.2 1.2 0.2
5.5 3.5 1.3 0.2
4.9 3.1 1.5 0.1
4.4 3.0 1.3 0.2
5.1 3.4 1.5 0.2
5.0 3.5 1.3 0.3
4.5 2.3 1.3 0.3
4.4 3.2 1.3 0.2
5.0 3.5 1.6 0.6
5.1 3.8 1.9 0.4
4.8 3.0 1.4 0.3
5.1 3.8 1.6 0.2
4.6 3.2 1.4 0.2
5.3 3.7 1.5 0.2
5.0 3.3 1.4 0.2
7.0 3.2 4.7 1.4
6.4 3.2 4.5 1.5
6.9 3.1 4.9 1.5
5.5 2.3 4.0 1.3
6.5 2.8 4.6 1.5
5.7 2.8 4.5 1.3
6.3 3.3 4.7 1.6
4.9 2.4 3.3 1.0
6.6 2.9 4.6 1.3
5.2 2.7 3.9 1.4
5.0 2.0 3.5 1.0
5.9 3.0 4.2 1.5
6.0 2.2 4.0 1.0
6.1 2.9 4.7 1.4
5.6 2.9 3.6 1.3
6.7 3.1 4.4 1.4
5.6 3.0 4.5 1.5
5.8 2.7 4.1 1.0
6.2 2.2 4.5 1.5
5.6 2.5 3.9 1.1
5.9 3.2 4.8 1.8
6.1 2.8 4.0 1.3
6.3 2.5 4.9 1.5
6.1 2.8 4.7 1.2
6.4 2.9 4.3 1.3
6.6 3.0 4.4 1.4
6.8 2.8 4.8 1.4
6.7 3.0 5.0 1.7
6.0 2.9 4.5 1.5
5.7 2.6 3.5 1.0
5.5 2.4 3.8 1.1
5.5 2.4 3.7 1.0
5.8 2.7 3.9 1.2
6.0 2.7 5.1 1.6
5.4 3.0 4.5 1.5
6.0 3.4 4.5 1.6
6.7 3.1 4.7 1.5
6.3 2.3 4.4 1.3
5.6 3.0 4.1 1.3
5.5 2.5 4.0 1.3
5.5 2.6 4.4 1.2
6.1 3.0 4.6 1.4
5.8 2.6 4.0 1.2
5.0 2.3 3.3 1.0
5.6 2.7 4.2 1.3
5.7 3.0 4.2 1.2
5.7 2.9 4.2 1.3
6.2 2.9 4.3 1.3
5.1 2.5 3.0 1.1
5.7 2.8 4.1 1.3
6.3 3.3 6.0 2.5
5.8 2.7 5.1 1.9
7.1 3.0 5.9 2.1
6.3 2.9 5.6 1.8
6.5 3.0 5.8 2.2
7.6 3.0 6.6 2.1
4.9 2.5 4.5 1.7
7.3 2.9 6.3 1.8
6.7 2.5 5.8 1.8
7.2 3.6 6.1 2.5
6.5 3.2 5.1 2.0
6.4 2.7 5.3 1.9
6.8 3.0 5.5 2.1
5.7 2.5 5.0 2.0
5.8 2.8 5.1 2.4
6.4 3.2 5.3 2.3
6.5 3.0 5.5 1.8
7.7 3.8 6.7 2.2
7.7 2.6 6.9 2.3
6.0 2.2 5.0 1.5
6.9 3.2 5.7 2.3
5.6 2.8 4.9 2.0
7.7 2.8 6.7 2.0
6.3 2.7 4.9 1.8
6.7 3.3 5.7 2.1
7.2 3.2 6.0 1.8
6.2 2.8 4.8 1.8
6.1 3.0 4.9 1.8
6.4 2.8 5.6 2.1
7.2 3.0 5.8 1.6
7.4 2.8 6.1 1.9
7.9 3.8 6.4 2.0
6.4 2.8 5.6 2.2
6.3 2.8 5.1 1.5
6.1 2.6 5.6 1.4
7.7 3.0 6.1 2.3
6.3 3.4 5.6 2.4
6.4 3.1 5.5 1.8
6.0 3.0 4.8 1.8
6.9 3.1 5.4 2.1
6.7 3.1 5.6 2.4
6.9 3.1 5.1 2.3
5.8 2.7 5.1 1.9
6.8 3.2 5.9 2.3
6.7 3.3 5.7 2.5
6.7 3.0 5.2 2.3
6.3 2.5 5.0 1.9
6.5 3.0 5.2 2.0
6.2 3.4 5.4 2.3
5.9 3.0 5.1 1.8
每一列減去該列均值後,得到矩陣B:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150-0.743333 0.446 -2.35867 -0.998667
-0.943333 -0.054 -2.35867 -0.998667
-1.14333 0.146 -2.45867 -0.998667
-1.24333 0.046 -2.25867 -0.998667
-0.843333 0.546 -2.35867 -0.998667
-0.443333 0.846 -2.05867 -0.798667
-1.24333 0.346 -2.35867 -0.898667
-0.843333 0.346 -2.25867 -0.998667
-1.44333 -0.154 -2.35867 -0.998667
-0.943333 0.046 -2.25867 -1.09867
-0.443333 0.646 -2.25867 -0.998667
-1.04333 0.346 -2.15867 -0.998667
-1.04333 -0.054 -2.35867 -1.09867
-1.54333 -0.054 -2.65867 -1.09867
-0.0433333 0.946 -2.55867 -0.998667
-0.143333 1.346 -2.25867 -0.798667
-0.443333 0.846 -2.45867 -0.798667
-0.743333 0.446 -2.35867 -0.898667
-0.143333 0.746 -2.05867 -0.898667
-0.743333 0.746 -2.25867 -0.898667
-0.443333 0.346 -2.05867 -0.998667
-0.743333 0.646 -2.25867 -0.798667
-1.24333 0.546 -2.75867 -0.998667
-0.743333 0.246 -2.05867 -0.698667
-1.04333 0.346 -1.85867 -0.998667
-0.843333 -0.054 -2.15867 -0.998667
-0.843333 0.346 -2.15867 -0.798667
-0.643333 0.446 -2.25867 -0.998667
-0.643333 0.346 -2.35867 -0.998667
-1.14333 0.146 -2.15867 -0.998667
-1.04333 0.046 -2.15867 -0.998667
-0.443333 0.346 -2.25867 -0.798667
-0.643333 1.046 -2.25867 -1.09867
-0.343333 1.146 -2.35867 -0.998667
-0.943333 0.046 -2.25867 -1.09867
-0.843333 0.146 -2.55867 -0.998667
-0.343333 0.446 -2.45867 -0.998667
-0.943333 0.046 -2.25867 -1.09867
-1.44333 -0.054 -2.45867 -0.998667
-0.743333 0.346 -2.25867 -0.998667
-0.843333 0.446 -2.45867 -0.898667
-1.34333 -0.754 -2.45867 -0.898667
-1.44333 0.146 -2.45867 -0.998667
-0.843333 0.446 -2.15867 -0.598667
-0.743333 0.746 -1.85867 -0.798667
-1.04333 -0.054 -2.35867 -0.898667
-0.743333 0.746 -2.15867 -0.998667
-1.24333 0.146 -2.35867 -0.998667
-0.543333 0.646 -2.25867 -0.998667
-0.843333 0.246 -2.35867 -0.998667
1.15667 0.146 0.941333 0.201333
0.556667 0.146 0.741333 0.301333
1.05667 0.046 1.14133 0.301333
-0.343333 -0.754 0.241333 0.101333
0.656667 -0.254 0.841333 0.301333
-0.143333 -0.254 0.741333 0.101333
0.456667 0.246 0.941333 0.401333
-0.943333 -0.654 -0.458667 -0.198667
0.756667 -0.154 0.841333 0.101333
-0.643333 -0.354 0.141333 0.201333
-0.843333 -1.054 -0.258667 -0.198667
0.0566667 -0.054 0.441333 0.301333
0.156667 -0.854 0.241333 -0.198667
0.256667 -0.154 0.941333 0.201333
-0.243333 -0.154 -0.158667 0.101333
0.856667 0.046 0.641333 0.201333
-0.243333 -0.054 0.741333 0.301333
-0.0433333 -0.354 0.341333 -0.198667
0.356667 -0.854 0.741333 0.301333
-0.243333 -0.554 0.141333 -0.0986667
0.0566667 0.146 1.04133 0.601333
0.256667 -0.254 0.241333 0.101333
0.456667 -0.554 1.14133 0.301333
0.256667 -0.254 0.941333 0.00133333
0.556667 -0.154 0.541333 0.101333
0.756667 -0.054 0.641333 0.201333
0.956667 -0.254 1.04133 0.201333
0.856667 -0.054 1.24133 0.501333
0.156667 -0.154 0.741333 0.301333
-0.143333 -0.454 -0.258667 -0.198667
-0.343333 -0.654 0.0413333 -0.0986667
-0.343333 -0.654 -0.0586667 -0.198667
-0.0433333 -0.354 0.141333 0.00133333
0.156667 -0.354 1.34133 0.401333
-0.443333 -0.054 0.741333 0.301333
0.156667 0.346 0.741333 0.401333
0.856667 0.046 0.941333 0.301333
0.456667 -0.754 0.641333 0.101333
-0.243333 -0.054 0.341333 0.101333
-0.343333 -0.554 0.241333 0.101333
-0.343333 -0.454 0.641333 0.00133333
0.256667 -0.054 0.841333 0.201333
-0.0433333 -0.454 0.241333 0.00133333
-0.843333 -0.754 -0.458667 -0.198667
-0.243333 -0.354 0.441333 0.101333
-0.143333 -0.054 0.441333 0.00133333
-0.143333 -0.154 0.441333 0.101333
0.356667 -0.154 0.541333 0.101333
-0.743333 -0.554 -0.758667 -0.0986667
-0.143333 -0.254 0.341333 0.101333
0.456667 0.246 2.24133 1.30133
-0.0433333 -0.354 1.34133 0.701333
1.25667 -0.054 2.14133 0.901333
0.456667 -0.154 1.84133 0.601333
0.656667 -0.054 2.04133 1.00133
1.75667 -0.054 2.84133 0.901333
-0.943333 -0.554 0.741333 0.501333
1.45667 -0.154 2.54133 0.601333
0.856667 -0.554 2.04133 0.601333
1.35667 0.546 2.34133 1.30133
0.656667 0.146 1.34133 0.801333
0.556667 -0.354 1.54133 0.701333
0.956667 -0.054 1.74133 0.901333
-0.143333 -0.554 1.24133 0.801333
-0.0433333 -0.254 1.34133 1.20133
0.556667 0.146 1.54133 1.10133
0.656667 -0.054 1.74133 0.601333
1.85667 0.746 2.94133 1.00133
1.85667 -0.454 3.14133 1.10133
0.156667 -0.854 1.24133 0.301333
1.05667 0.146 1.94133 1.10133
-0.243333 -0.254 1.14133 0.801333
1.85667 -0.254 2.94133 0.801333
0.456667 -0.354 1.14133 0.601333
0.856667 0.246 1.94133 0.901333
1.35667 0.146 2.24133 0.601333
0.356667 -0.254 1.04133 0.601333
0.256667 -0.054 1.14133 0.601333
0.556667 -0.254 1.84133 0.901333
1.35667 -0.054 2.04133 0.401333
1.55667 -0.254 2.34133 0.701333
2.05667 0.746 2.64133 0.801333
0.556667 -0.254 1.84133 1.00133
0.456667 -0.254 1.34133 0.301333
0.256667 -0.454 1.84133 0.201333
1.85667 -0.054 2.34133 1.10133
0.456667 0.346 1.84133 1.20133
0.556667 0.046 1.74133 0.601333
0.156667 -0.054 1.04133 0.601333
1.05667 0.046 1.64133 0.901333
0.856667 0.046 1.84133 1.20133
1.05667 0.046 1.34133 1.10133
-0.0433333 -0.354 1.34133 0.701333
0.956667 0.146 2.14133 1.10133
0.856667 0.246 1.94133 1.30133
0.856667 -0.054 1.44133 1.10133
0.456667 -0.554 1.24133 0.701333
0.656667 -0.054 1.44133 0.801333
0.356667 0.346 1.64133 1.10133
0.0566667 -0.054 1.34133 0.601333
2.計算B的協方差矩陣C:
1 2 3 40.685694 -0.0392685 1.27368 0.516904
-0.0392685 0.188004 -0.321713 -0.117981
1.27368 -0.321713 3.11318 1.29639
0.516904 -0.117981 1.29639 0.582414
3.計算協方差矩陣C的特征值和特征向量。
C=V*S*V-1
S=
4.2248414 0 0 0
0 0.24224437 0 0
0 0 0.078524387 0
0 0 0 0.023681839
V=
0.36158919 0.65654382 -0.58100304 0.3172364
-0.082268924 0.72970845 0.596429220 -0.3240827
0.85657212 -0.17576972 0. 072535217 -0.47971643
0.35884438 -0.074704743 0.54904125 0.75113489
2.8271335 5.6413345
2.7959501 5.1451715
2.6215213 5.1773814
2.7649037 5.0036022
2.7827477 5.648651
3.2314432 6.0625092
2.6904502 5.2326213
2.8848587 5.4851323
2.6233824 4.7439288
2.837496 5.2080359
3.0048137 5.9666624
2.898198 5.3362466
2.7239067 5.0869876
2.2861405 4.8114466
2.867797 6.5009233
3.127471 6.6594805
2.8888143 6.132817
2.8630179 5.633864
3.3122624 6.1939719
2.9239945 5.8351996
3.2008088 5.7125959
2.9681058 5.7547583
2.2954831 5.4563413
3.2082122 5.4202505
3.1551697 5.2835156
3.0034234 5.1756719
3.0422848 5.4526144
2.9489496 5.6894119
2.8715193 5.634018
2.8784929 5.1246505
2.9228787 5.117334
3.1012632 5.7328089
2.8637038 6.1347075
2.9141809 6.4147479
2.837496 5.2080359
2.6443408 5.3919215
2.8861119 5.921529
2.837496 5.2080359
2.5294983 4.8344766
2.9210176 5.5507867
2.7412018 5.5857866
2.6591299 4.3818646
2.5130445 4.9804183
3.1058267 5.5106443
3.3025077 5.7574212
2.7956756 5.0720467
2.9737672 5.8250931
2.6710196 5.0941501
2.9686547 5.901008
2.8074283 5.4297384
6.7961349 6.0001695
6.4437514 5.6339266
6.9754017 5.8189198
5.6923082 4.4891254
6.5984751 5.3901207
6.1517776 4.8974035
6.6065644 5.5986187
4.759874 4.3136202
6.5546382 5.5436868
5.5011511 4.5941521
5.0002549 4.0522372
6.0224389 5.2124439
5.7736764 4.7668379
6.4953853 5.1903675
5.3364769 5.0629127
6.4389134 5.7829664
6.1709338 4.9627499
5.7458813 4.9828064
6.4537025 4.7729094
5.5545872 4.7332394
6.6275817 5.2305124
5.8681272 5.2479059
6.8078095 4.9871684
6.4318433 5.1323376
6.2253487 5.465109
6.4109813 5.6443412
6.8423818 5.5594003
7.0687368 5.5821223
6.3237964 5.1523966
5.204006 4.949643
5.440998 4.6121911
5.3194564 4.6372386
5.6463357 5.0030194
6.8900779 4.8935226
6.098616 4.8314411
6.3185463 5.5097803
6.7317694 5.722765
6.3242084 4.9440526
5.7565361 5.0479987
5.6758544 4.6350671
5.9743719 4.6452005
6.4015012 5.2809153
5.7402198 4.9124716
4.8042598 4.3063037
5.866874 4.8115092
5.8424678 5.1035466
5.8865791 5.0231053
6.1530309 5.3338002
4.6028777 4.5631602
5.8091488 4.9677114
8.0430681 5.3028838
6.9254133 4.7398024
8.1278252 5.6566652
7.4821558 5.1336016
7.8610989 5.2728454
8.9082203 5.8618983
6.0307247 4.123374
8.4433454 5.6671066
7.8310134 5.0691818
8.4294749 6.0951088
7.1732758 5.5567668
7.3136813 5.0985747
7.6767196 5.5300099
6.8559354 4.5383128
7.0966086 4.7754209
7.4160846 5.4335471
7.4605895 5.3554582
9.0001057 6.486272
9.3060273 5.5679974
6.8096707 4.5537158
7.939508 5.6915111
6.7094386 4.7091479
9.0106057 5.7715045
6.8990091 5.1106987
7.7871944 5.6481141
8.1255342 5.8730957
6.7689661 5.1355922
6.8020106 5.1983025
7.6341949 5.1038737
7.8989047 5.7772489
8.3523013 5.6874736
8.743683 6.6852526
7.6700793 5.0964032
6.9544433 5.170927
7.2909809 4.8132622
8.587862 6.0004966
7.6563279 5.453633
7.4162037 5.3627746
6.6801944 5.1502251
7.6189944 5.6862121
7.8256443 5.497338
7.4337916 5.7240021
6.9254133 4.7398024
8.0746635 5.5907028
7.9307322 5.6182322
7.4553579 5.5021455
7.0370045 4.9397096
7.2753867 5.3932482
7.4129702 5.430603
6.9010071 5.0318398
每個樣本正好是二維的,畫在平面坐標系中如圖:
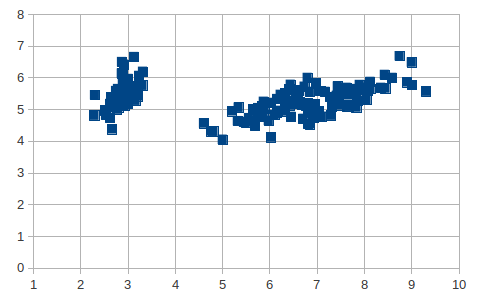
鹫尾花數據集共分為3類花(前50個樣本為一類,中間50個樣本為一類,後50個樣本為一類),從上圖可以看到把數據集映射到2維後分類會更容易進行,直觀上看已經是線性可分的了,下面我們用自組織映射網絡對其進行聚類。
當然我們已知了有3類,所以在設計SOFM網絡時,我把競爭層節點數設為3,此時的聚類結果是前50個樣本聚為一類,後100個樣本聚為一類。當把競爭層節點數改為4時,僅第2類中的3個樣本被誤分到了第3類中,整體精度達98%!
#include<iostream>
#include<fstream>
#include<set>
#include<cstdlib>
#include<vector>
#include<cmath>
#include<ctime>
using namespace std;
const int sample_num=150; //鹫尾花樣本個數
const int class_num=4; //指定聚類的數目
int iteration_ceil; //迭代的上限
vector<pair<double,double> > flowers(sample_num); //樣本數據
vector<vector<double> > weight(class_num); //權向量
const double prime_eta=0.7; //初始學習率
/*向量模長歸一化*/
void normalize(vector<double> &vec){
double sum=0.0;
for(int i=0;i<vec.size();++i)
sum+=pow(vec[i],2);
sum=sqrt(sum);
for(int i=0;i<vec.size();++i)
vec[i]/=sum;
}
/*從文件讀入鹫尾花樣本數據*/
void init_sample(string filename){
ifstream ifs(filename.c_str());
if(!ifs){
cerr<<"open data file failed."<<endl;
exit(1);
}
for(int i=0;i<sample_num;++i){
vector<double> X(2);
ifs>>X[0]>>X[1];
normalize(X); //輸入向量模長歸一化
flowers[i]=make_pair(X[0],X[1]);
}
ifs.close();
}
/*初始化權值*/
void init_weight(){
srand(time(0));
for(int i=0;i<weight.size();++i){
vector<double> ele(2);
ele[0]=rand()/(double)RAND_MAX;
ele[1]=rand()/(double)RAND_MAX;
normalize(ele); //權值向量模長歸一化
weight[i]=ele;
}
}
/*根據輸入,選擇獲勝者*/
int pick_winner(double x1,double x2){
int rect=-1;
double max=0.0;
for(int i=0;i<weight.size();++i){
double product=x1*weight[i][0]+x2*weight[i][1];
if(product>max){
max=product;
rect=i;
}
}
return rect;
}
int main(int argc,char *argv[]){
cout<<"input iteration count"<<endl;
int count; //每個樣本迭代的次數
cin>>count;
cout<<"input data file name"<<endl;
string filename;
cin>>filename;
iteration_ceil=count*sample_num;
init_sample(filename);
init_weight();
double eta=prime_eta;
double gradient1=-1*9*prime_eta/iteration_ceil;
double gradient2=-1*prime_eta/(9*iteration_ceil);
double b1=prime_eta;
double b2=prime_eta/9;
for(int iteration=0;iteration<iteration_ceil;++iteration){
int flower_index=iteration%sample_num;
double x1=flowers[flower_index].first;
double x2=flowers[flower_index].second;
int winner=pick_winner(x1,x2);
/*更改獲勝者的權值*/
weight[winner][0]+=eta*(x1-weight[winner][0]);
weight[winner][1]+=eta*(x2-weight[winner][1]);
/*權向量歸一化*/
for(int i=0;i<weight.size();++i){
vector<double> W(2);
W[0]=weight[i][0];
W[1]=weight[i][1];
normalize(W);
weight[i][0]=W[0];
weight[i][1]=W[1];
}
/*更新學習率*/
if(iteration<0.1*iteration_ceil){ //在前10%的迭代中,學習率線性下降到原來的10%
eta=gradient1*iteration+b1;
}
else{ //後90%的迭代中線性降低到0
eta=gradient2*iteration+b2;
}
}
for(int i=0;i<sample_num;++i){
double x1=flowers[i].first;
double x2=flowers[i].second;
int winner=pick_winner(x1,x2);
cout<<i+1<<"\t"<<winner+1<<endl;
}
return 0;
}
輸出聚類結果:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 1501 2
2 2
3 2
4 2
5 2
6 2
7 2
8 2
9 2
10 2
11 2
12 2
13 2
14 2
15 2
16 2
17 2
18 2
19 2
20 2
21 2
22 2
23 2
24 2
25 2
26 2
27 2
28 2
29 2
30 2
31 2
32 2
33 2
34 2
35 2
36 2
37 2
38 2
39 2
40 2
41 2
42 2
43 2
44 2
45 2
46 2
47 2
48 2
49 2
50 2
51 4
52 4
53 4
54 4
55 4
56 4
57 4
58 4
59 4
60 4
61 4
62 4
63 4
64 4
65 4
66 4
67 4
68 4
69 1
70 4
71 4
72 4
73 1
74 4
75 4
76 4
77 4
78 4
79 4
80 4
81 4
82 4
83 4
84 1
85 4
86 4
87 4
88 4
89 4
90 4
91 4
92 4
93 4
94 4
95 4
96 4
97 4
98 4
99 4
100 4
101 1
102 1
103 1
104 1
105 1
106 1
107 1
108 1
109 1
110 1
111 1
112 1
113 1
114 1
115 1
116 1
117 1
118 1
119 1
120 1
121 1
122 1
123 1
124 1
125 1
126 1
127 1
128 1
129 1
130 1
131 1
132 1
133 1
134 1
135 1
136 1
137 1
138 1
139 1
140 1
141 1
142 1
143 1
144 1
145 1
146 1
147 1
148 1
149 1
150 1