LeetCode Largest Rectangle in Histogram

LeetCode解題之Largest Rectangle in Histogram

原題

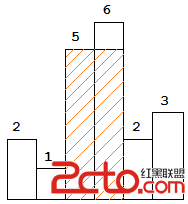
給定一個柱狀圖，求它能包含的最大的矩形的面積。如下圖中陰影部分就是要求的矩形。

注意點：

例子：

輸入: heights = [2,1,5,6,2,3]

輸出: 10

解題思路

這道題卡了很久，一直沒想到好的解決方案。查了一些資料，比較優雅的方法是通過棧來解決。

首先明確最終矩形的高度一定是某一個柱的高度，以上面的例子為例，可能是2,1,5,6,2,3中的一個，如果像這樣把每個柱窮舉出來，並嘗試向兩邊擴展來得到最大面積，時間復雜度就太大。仔細想一想，為什麼要嘗試向兩邊擴展，如例子中的第二個2（以它為高的話最多可以涵蓋4個柱），因為它的左右兩邊相鄰的柱都有比它高的，也就是說柱的高度不是有序的，如果我們能得到一個有序遞增的排列，那麼就只要像右擴展，而不要向左擴展了，因為左邊的柱比它自己低。

依次遍歷柱狀結構，如果是遞增的則壓棧，如果不是則把比它高的柱依次彈出（只彈出比當前柱高的可以保證把當前柱壓棧後，棧中的柱依舊是依次遞增的），並計算以該柱為高的矩形的面積。計算面積時，寬度應該是棧頂元素到遍歷到元素之間的寬，如當彈出第二個2（2後面沒有比它小的元素，為了使該元素能順利彈出，在原柱狀圖末尾加一個0）時，棧頂元素是1，這樣就能方便計算出寬度為4。還有一個問題是彈出1時棧中沒有元素，無法計算寬度，所以在初始化時要在棧底加一個-1來應對所有元素都出棧的情況。

AC源碼

class Solution(object):
    def largestRectangleArea(self, heights):
        """
        :type heights: List[int]
        :rtype: int
        """
        heights.append(0)
        stack = [-1]
        result = 0
        for i in range(len(heights)):
            while heights[i] < heights[stack[-1]]:
                h = heights[stack.pop()]
                w = i - stack[-1] - 1
                result = max(result, h * w)
            stack.append(i)
        heights.pop()
        return result


if __name__ == "__main__":
    assert Solution().largestRectangleArea([2, 1, 5, 6, 2, 3]) == 10