LeetCode 88 Merge Sorted Array（合並排序數組）（*）

LeetCode 88 Merge Sorted Array（合並排序數組）（*）

翻譯

給定兩個排序的整型數組nums1和nums2，將nums2合並到nums1成一個排序數組。

批注：
你可以假設nums1中有足夠的空間（空間大於或等於m+n）來存放來自nums2的額外元素。
nums1和nums2的初始空間分別是m和n。

原文

Given two sorted integer arrays nums1 and nums2, merge nums2 into nums1 as one sorted array.

Note:
You may assume that nums1 has enough space (size that is greater or equal to m + n) to hold additional elements from nums2. 

The number of elements initialized in nums1 and nums2 are m and n respectively.

分析

有一種思路是，另外設置一個數組，然後將nums1和nums2中的數據按大小逐個添加到這個新數組中，最後將這個數組整個賦值給nums1，不過像是作弊一樣，題意說了是要並到nums1中的，這樣一來nums1並沒有變化。

所以，繼續想新的方法……

先來理一理，有如下這些關系：

1，m和n表示的是nums1和nums2中已經初始化的元素數量，
而並非nums1和nums2的空間大小，也就是說nums1中空間足夠大，
但其中m個空間設置了該設的值，我們在本題中稱它為有效數目

2，由1得出合並後的總的有效數目為m+n

3，因為都是從0開始，所以nums1和nums2的最後一個元素的索引分別是m-1和n-1，
合並後的nums1的最後一個元素的索引應該是m+n-1

4，我們是將nums2並入nums1，所以整體的循環可以從nums2開始

5，下面我會闡述為什麼內部的循環要從nums1的尾部開始：

因為這是vector數組而不是鏈表，它們是有索引的，索引是從前到後的（從0到m-1）
如果在數組前方添加一個數字，那麼其後的所有元素都需要往後挪一步
而如果在後方添加一個數字，前面的則不需要移動。
至於為什麼不擔心後方空間問題，因為題目說了給nums1的空間足夠大。

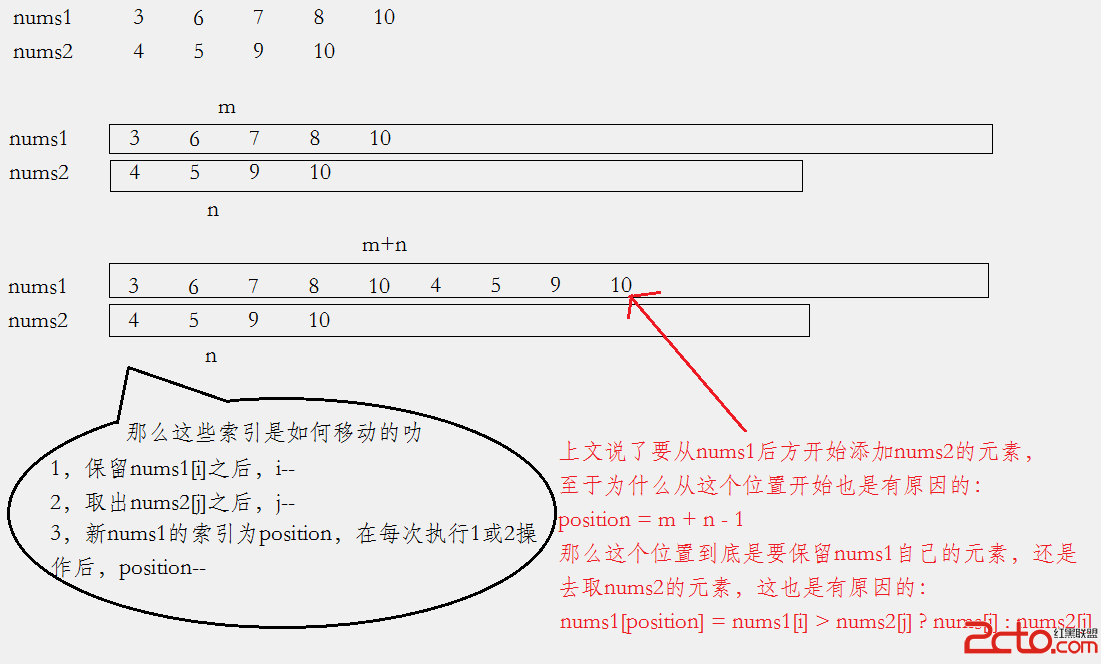
原諒我沒有再給數組畫豎線以區分每個格子，相信大家都懂的，我已經盡力了，哈哈……

看代碼……

代碼

class Solution {
public:
    void merge(vector &nums1, int m, vector &nums2, int n) {
        int i = m - 1, j = n - 1, position = m + n - 1;
        while (j >= 0) {
            nums1[position--] = i >= 0 && nums1[i] > nums2[j] ? nums1[i--] : nums2[j--];
        }
    }
};