LeetCode Sqrt(x)

LeetCode解題之Sqrt(x)

原題

求一個數的平方根。

注意點：

例子：

輸入: x = 5

輸出: 2

解題思路

采用牛頓迭代法，通過逼近來求方程 y=x^2+a 的解。接單介紹一下牛頓迭代法，如下圖，求方程曲線與y軸的交點就是方程的解。隨意取一個值 X0 ，找出曲線在 X0 處的切線，該切線與y軸的交點為 X1 ，再求 X1 處的切線的交點，可以看出來交點會不斷的向目標值靠近，現在確定一個阈值就可以找出近似解了。由於平方根是正數，所以初始的取值應為一個正數。

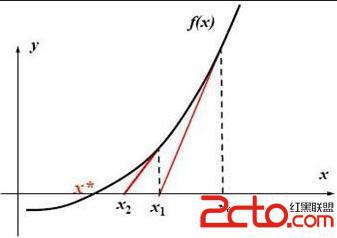
注：圖片來源於搜索引擎

AC源碼

class Solution(object):
    def mySqrt(self, x):
        """
        :type x: int
        :rtype: int
        """
        result = 1.0
        while abs(result * result - x) > 0.1:
            result = (result + x / result) / 2
        return int(result)


if __name__ == "__main__":
    assert Solution().mySqrt(5) == 2
    assert Solution().mySqrt(0) == 0