Codeforces Round #335 (Div. 2)B. Testing Robots解題報告，

Codeforces Round #335 (Div. 2)B. Testing Robots解題報告，

                                                                                           B. Testing Robots time limit per test 2 seconds memory limit per test 256 megabytes input standard input output standard output

The Cybernetics Failures (CF) organisation made a prototype of a bomb technician robot. To find the possible problems it was decided to carry out a series of tests. At the beginning of each test the robot prototype will be placed in cell (x₀, y₀) of a rectangular squared field of size x × y, after that a mine will be installed into one of the squares of the field. It is supposed to conduct exactly x·y tests, each time a mine is installed into a square that has never been used before. The starting cell of the robot always remains the same.

After placing the objects on the field the robot will have to run a sequence of commands given by string s, consisting only of characters 'L', 'R', 'U', 'D'. These commands tell the robot to move one square to the left, to the right, up or down, or stay idle if moving in the given direction is impossible. As soon as the robot fulfills all the sequence of commands, it will blow up due to a bug in the code. But if at some moment of time the robot is at the same square with the mine, it will also blow up, but not due to a bug in the code.

Moving to the left decreases coordinate y, and moving to the right increases it. Similarly, moving up decreases the x coordinate, and moving down increases it.

The tests can go on for very long, so your task is to predict their results. For each k from 0 to length(s) your task is to find in how many tests the robot will run exactly k commands before it blows up.

Input

The first line of the input contains four integers x, y, x₀, y₀ (1 ≤ x, y ≤ 500, 1 ≤ x₀ ≤ x, 1 ≤ y₀ ≤ y) — the sizes of the field and the starting coordinates of the robot. The coordinate axis X is directed downwards and axis Y is directed to the right.

The second line contains a sequence of commands s, which should be fulfilled by the robot. It has length from 1 to 100 000 characters and only consists of characters 'L', 'R', 'U', 'D'.

Output

Print the sequence consisting of (length(s) + 1) numbers. On the k-th position, starting with zero, print the number of tests where the robot will run exactly k commands before it blows up.

Sample test(s) Input

3 4 2 2
UURDRDRL

Output

1 1 0 1 1 1 1 0 6

Input

2 2 2 2
ULD

Output

1 1 1 1

Note

In the first sample, if we exclude the probable impact of the mines, the robot's route will look like that: .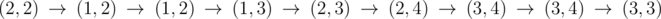

 

對於這題筆者認為就是簡單的模擬題：

但是在這千萬不能用數組和循環結構的形式來解決實現這個問題，因為有可能會導致RuntimeError；

下面就貼出筆者的代碼：

#include<iostream>
#include<stdio.h>
#include<stdlib.h>
#include<memory.h>
#include<string.h>
#include<algorithm>
#include<cmath>
const int N = 30;
const int inf=-100000;
using namespace std;

int g[510][510];
int num;
int X,Y,X0,Y0,xx,yy;
int fun(char c)
{
int flag=0;
switch(c)
{
case'R':
if(yy<Y)
yy++;
break;
case'L':
if(yy>1)
yy--;
break;
case'U':
if(xx>1)
xx--;
break;
case'D':
if(xx<X)
xx++;
break;
}
if(g[xx][yy]==0)
{
flag=1;
num--;
}
g[xx][yy]=1;
return flag;
}
int main()
{
//int x,y,x0,y0;
char str[100010];
scanf("%d%d%d%d",&X,&Y,&X0,&Y0);
scanf("%s",str);
memset(g,0,sizeof(g));
num=X*Y;
num--;
xx=X0,yy=Y0;
g[X0][Y0]=1;
cout<<"1 ";
for(int i=0;i<strlen(str)-1;i++)
{
cout<<fun(str[i])<<" ";
}
if(fun(str[strlen(str)-1]))
{
num++;
cout<<num<<endl;
}
else
{
cout<<num<<endl;
}
return 0;
}