十八世紀,數學家們研究出了許多計算圓周率的無窮級數,其中,牛頓研究出的一個級數是:
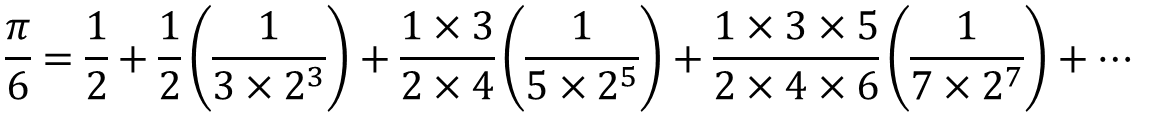
利用這個無窮級數,計算圓周率到小數點後15位。
方法:對上述公式作如下簡單變形,就可以方便地編寫程序了。
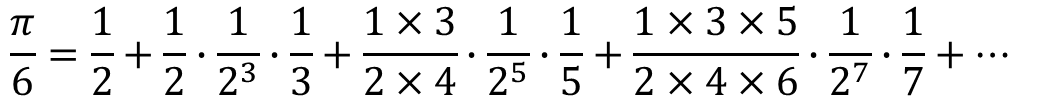
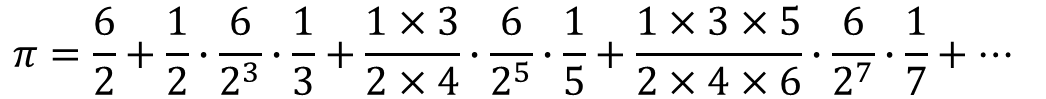
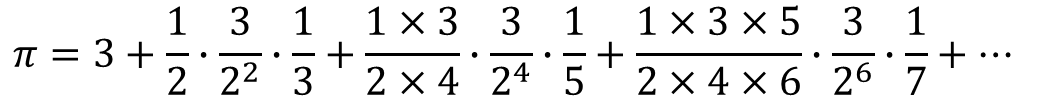
1 #include <iostream>
2 #include <iomanip>
3 using namespace std;
4
5 int main( void ) /* name: Pinew.cpp */
6 { double s, t, p;
7 int a, b, n;
8 s=3.0; t=3.0; a=1; b=2; n=0;
9 cout<<fixed<<setprecision(15);
10 do
11 { t=0.25*t*a/b;
12 p=t/(a+2);
13 s+=p;
14 n++;
15 cout<<"n="<<setw(4)<<n<<" Pi="<<s<<endl;
16 a+=2;
17 b+=2;
18 }while(p>=1E-18);
19
20 return 0;
21 }
運行結果:
n= 1 Pi=3.125000000000000
n= 2 Pi=3.139062500000000
n= 3 Pi=3.141155133928572
n= 4 Pi=3.141511172340030
n= 5 Pi=3.141576715774867
n= 6 Pi=3.141589425319122
n= 7 Pi=3.141591982358383
n= 8 Pi=3.141592511157862
n= 9 Pi=3.141592622870617
n= 10 Pi=3.141592646875561
n= 11 Pi=3.141592652105887
n= 12 Pi=3.141592653258738
n= 13 Pi=3.141592653515338
n= 14 Pi=3.141592653572930
n= 15 Pi=3.141592653585950
n= 16 Pi=3.141592653588912
n= 17 Pi=3.141592653589590
n= 18 Pi=3.141592653589746
n= 19 Pi=3.141592653589782
n= 20 Pi=3.141592653589790
n= 21 Pi=3.141592653589792
n= 22 Pi=3.141592653589793
n= 23 Pi=3.141592653589793
n= 24 Pi=3.141592653589793
n= 25 Pi=3.141592653589793
n= 26 Pi=3.141592653589793
n= 27 Pi=3.141592653589793