LCS(Longest Common Subsequence 最長公共子序列),lcssubsequence
問題描述
最長公共子序列,英文縮寫為LCS(Longest Com

![]()
#include <bits/stdc++.h>
const int MAX=1010;
char x[MAX];
char y[MAX];
int DP[MAX][MAX];
int b[MAX][MAX];
using namespace std;
int PRINT_LCS(int b[][MAX],char *x,int i,int j)
{
if(i==0||j==0)
return 1;
if(b[i][j]==1)
{
PRINT_LCS(b,x,i-1,j-1);
cout<<x[i]<<" ";
}
else if(b[i][j]==2)
{
PRINT_LCS(b,x,i-1,j);
}
else if(b[i][j]==3)
{
PRINT_LCS(b,x,i,j-1);
}
}
int main()
{
int T;
int n,m,i,j;
cin>>T;
while(T--)
{
while(cin>>n>>m)
{
for(int i=1; i<=n; i++)
cin>>x[i];
for(int j=1; j<=m; j++)
cin>>y[j];
memset(DP,0,sizeof(DP));
for(i=1; i<=n; i++)
{
for(j=1; j<=m; j++)
{
if(x[i]==y[j])
{
DP[i][j]=DP[i-1][j-1]+1;
b[i][j]=1;
}
else if(DP[i-1][j]>=DP[i][j-1])
{
DP[i][j]=DP[i-1][j];
b[i][j]=2;
}
else
{
DP[i][j]=DP[i][j-1];//Max(DP[i-1][j],DP[i][j-1]);
b[i][j]=3;
}
}
}
cout<<DP[n][m]<<endl;
PRINT_LCS(b,x,n,m);
cout<<endl;
}
}
return 0;
}
View Code
mon Subsequence)。其定義是,一個序列 S ,如果分別是兩個或多個已知序列的子序列,且是所有符合此條件序列中最長的,則 S 稱為已知序列的最長公共子序列。而最長公共子串(要求連續)和最長公共子序列是不同的
應用
最長公共子序列是一個十分實用的問題,它可以描述兩段文字之間的“相似度”,即它們的雷同程度,從而能夠用來辨別抄襲。對一段文字進行修改之後,計算改動前後文字的最長公共子序列,將除此子序列外的部分提取出來,這種方法判斷修改的部分,往往十分准確。簡而言之,百度知道、百度百科都用得上。
動態規劃
第一步:先計算最長公共子序列的長度。
第二步:根據長度,然後通過回溯求出最長公共子序列。
現有兩個序列X={x1,x2,x3,...xi},Y={y1,y2,y3,....,yi},
設一個C[i,j]: 保存Xi與Yj的LCS的長度。
遞推方程為:
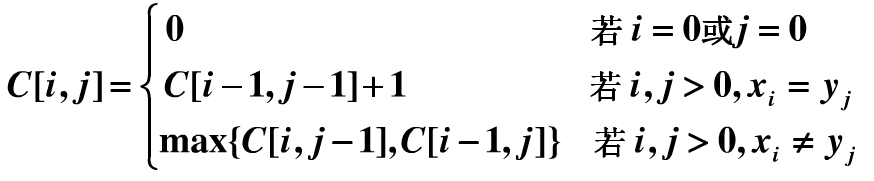
代碼親測: