leetcode筆記：Interlaving String

leetcode筆記：Interlaving String

一. 題目描述

Given s1; s2; s3, find whether s3 is formed by the interleaving of s1 and s2.
For example, Given: s1 = “aabcc”, s2 = “dbbca”,
When s3 = “aadbbcbcac”, return true.
When s3 = “aadbbbaccc”, return false.

二. 題目分析

此題可使用二維動態規劃來解決，下表給出了直觀的匹配過程：

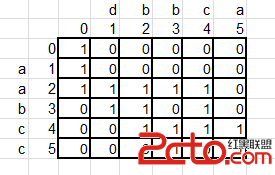
設某一格的狀態為k[i][j]，表示s1[i]或s2[j]，與s3[i+j]的匹配結果。s3可與s1和s2相匹配時，可分為以下兩種情況：

如果s1 的最後一個字符等於s3 的最後一個字符，則k[i][j]=k[i-1][j]；
如果s2 的最後一個字符等於s3 的最後一個字符，則k[i][j]=k[i][j-1]。

因此狀態轉移方程如下：
f[i][j] = (s1[i - 1] == s3 [i + j - 1] && f[i - 1][j]) "| (s2[j - 1] == s3 [i + j - 1] && f[i][j - 1]);

三. 示例代碼

#include 
#include 
#include 

using namespace std;

class Solution
{
public:
     bool isInterleave(string s1, string s2, string s3)
     {
         if (s3.size() != s1.size() + s2.size())
            return false;
         if (s3[0] != s1[0] && s3[0] != s2[0])
            return false;

         vector > k(s1.size() + 1, vector(s2.size() + 1, false));
         k[0][0] = true;

         // 邊界設置
         for (size_t i = 1; i <= s1.size(); ++i)
             k[i][0] = (s1[i - 1] == s3[i - 1]) && k[i - 1][0];

         for (size_t j = 1; j <= s2.size(); ++j)
             k[0][j] = (s2[j - 1] == s3[j - 1]) && k[0][j - 1];

         for (size_t i = 1; i <= s1.size(); ++i)
         {
             for (size_t j = 1; j <= s2.size(); ++j)
             {
                 k[i][j] = ((s1[i - 1] == s3[i + j - 1]) && k[i - 1][j]) ||
                           ((s2[j - 1] == s3[i + j - 1]) && k[i][j - 1]);
             }
         }

         return k[s1.size()][s2.size()];
     }
};

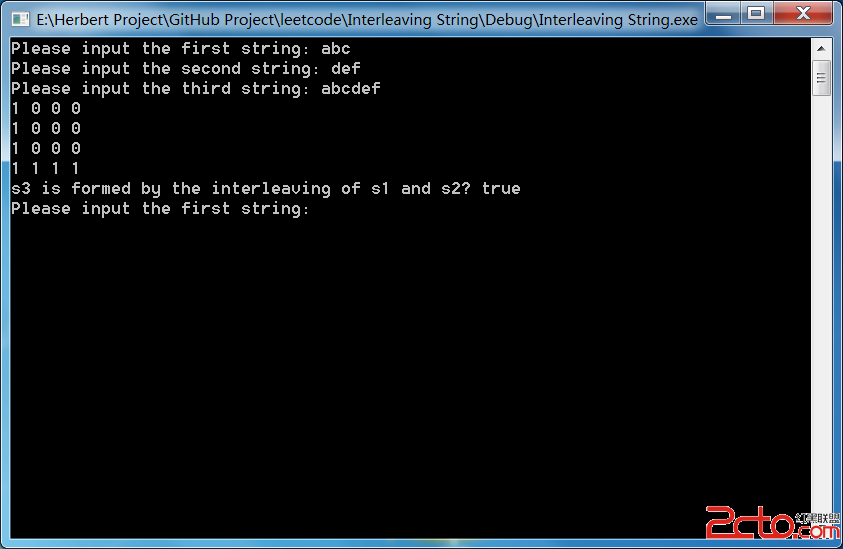
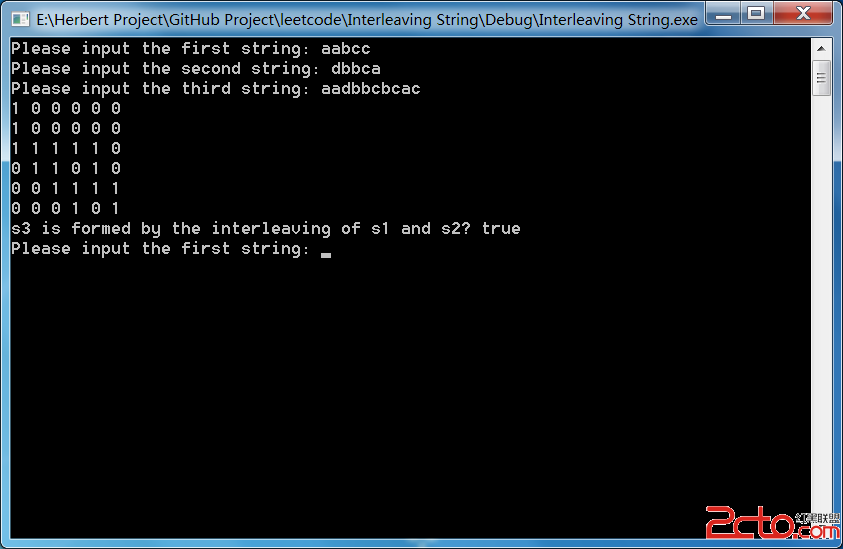編程時要注意邊界條件的問題和數組的下標問題。