ZOJ2412，

ZOJ2412，

Benny has a spacious farm land to irrigate. The farm land is a rectangle, and is divided into a lot of samll squares. Water pipes are placed in these squares. Different square has a different type of pipe. There are 11 types of pipes, which is marked from A to K, as Figure 1 shows.

Figure 1

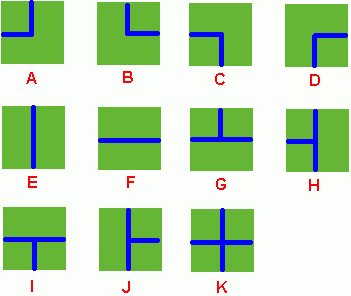
Benny has a map of his farm, which is an array of marks denoting the distribution of water pipes over the whole farm. For example, if he has a map

ADC
FJK
IHE

then the water pipes are distributed like

Figure 2

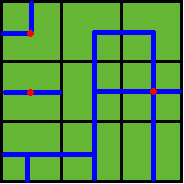
Several wellsprings are found in the center of some squares, so water can flow along the pipes from one square to another. If water flow crosses one square, the whole farm land in this square is irrigated and will have a good harvest in autumn.

Now Benny wants to know at least how many wellsprings should be found to have the whole farm land irrigated. Can you help him?

Note: In the above example, at least 3 wellsprings are needed, as those red points in Figure 2 show.

Input

There are several test cases! In each test case, the first line contains 2 integers M and N, then M lines follow. In each of these lines, there are N characters, in the range of 'A' to 'K', denoting the type of water pipe over the corresponding square. A negative M or N denotes the end of input, else you can assume 1 <= M, N <= 50.

Output

For each test case, output in one line the least number of wellsprings needed.

Sample Input

2 2
DK
HF

3 3
ADC
FJK
IHE

-1 -1

Sample Output

2
3

題目鏈接：http://acm.zju.edu.cn/onlinejudge/showProblem.do?problemCode=2412

簡單的dfs搜索，主要就是構圖，將水管狀態變為數組狀態，可以將水管類型字母轉化成3*3的方陣。

0,1,0,　　　　0,1,0,　　　　0,0,0,　　　　0,0,0,　　　　0,1,0,　　　0,0,0,　　　　0,1,0,　　　　0,1,0,　　　　0,0,0,　　　　0,1,0,　　　　0,1,0,

1,1,0,　　　　0,1,1,　　　　1,1,0,　　　　0,1,1,　　　　0,1,0,　　　1,1,1,　　　　1,1,1,　　　　1,1,0,　　　　1,1,1,　　　　0,1,1,　　　　1,1,1,

0,0,0,　　　　0,0,0,　　　　0,1,0,　　　　0,1,0,　　　　0,1,0,　　　0,0,0,　　　　0,0,0,　　　　0,1,0,　　　　0,1,0,　　　　0,1,0,　　　　0,1,0

   A　　　　　　B    　　　　　C　　　　　　  D　　　　　　E　　　　　 F　　　　　　 G　　　　　　 H　　　　　　 I　　　　　　　J　　　　　　K

構圖成功後就是簡單的dfs。類似題目有HDOJ1241，HDOJ1312，POJ1562，POJ2386，POJ1979

#include<iostream>
#include<cstdio>
#include<cstring>
using namespace std;
int n,m;
int farm[155][155];
int dir[4][2]= {{1,0},{0,1},{-1,0},{0,-1}};
int x[11][9]=
{
    0,1,0,1,1,0,0,0,0,
    0,1,0,0,1,1,0,0,0,
    0,0,0,1,1,0,0,1,0,
    0,0,0,0,1,1,0,1,0,
    0,1,0,0,1,0,0,1,0,
    0,0,0,1,1,1,0,0,0,
    0,1,0,1,1,1,0,0,0,
    0,1,0,1,1,0,0,1,0,
    0,0,0,1,1,1,0,1,0,
    0,1,0,0,1,1,0,1,0,
    0,1,0,1,1,1,0,1,0
};
void build(char c,int signi,int signj);
void dfs(int x,int y);
int main()
{
    int i,j;
    char c;
    while(scanf("%d%d",&n,&m)&&n>=0&&m>=0)
    {
        getchar();
        memset(farm,0,sizeof(farm));
        for(i=1; i<n*3-1; i+=3)
        {
            for(j=1; j<m*3-1; j+=3)
            {
                scanf("%c",&c);
                build(c,i,j);
                //cout<<i<<" "<<j<<endl;
            }
            getchar();
        }
        /*
        cout<<endl;
        for(i=0; i<n*3; i++)
        {
            for(j=0; j<m*3; j++)
                printf("%d",farm[i][j]);
            printf("\n");
        }
        cout<<endl;
        */
        int sum=0;
        for(i=0; i<n*3; i++)
            for(j=0; j<m*3; j++)
                if(farm[i][j]==1)
                {
                    farm[i][j]=0;
                    sum++;
                    dfs(i,j);
                }
        cout<<sum<<endl;
    }
    return 0;
}
void build(char c,int signi,int signj)
{
    int i,j;
    int k,t=0;
    k=c-65;
    for(i=signi-1; i<=signi+1; i++)
    {
        for(j=signj-1; j<=signj+1; j++)
        {
            farm[i][j]=x[k][t++];
            //printf("%d",farm[i][j]);
        }
        //printf("\n");
    }
}
void dfs(int x,int y)
{
    int i,fx,fy;
    for(i=0; i<4; i++)
    {
        fx=x+dir[i][0];
        fy=y+dir[i][1];
        if(fx>=0&&fx<n*3&&fy>=0&&fy<m*3&&farm[fx][fy]==1)
        {
            farm[fx][fy]=0;
            dfs(fx,fy);
        }
    }
}