abcfbc abfcab
programming contest 
abcd mnp

4
2
0

鏈接：http://acm.hdu.edu.cn/showproblem.php?pid=1159

題意：求兩個字符串的最長公共子串。

思路：動態規劃。

最長公共子序列是一個很經典的動態規劃問題，最近正在學習動態規劃，所以拿來這裡再整理一下。

這個問題在《算法導論》中作為講動態規劃算法的例題出現。

動態規劃，眾所周知，第一步就是找子問題，也就是把一個大的問題分解成子問題。這裡我們設兩個字符串A、B，A = a0, a1, a2, ..., am-1，B = b0, b1, b2, ..., bn-1。

（1）如果am-1 == bn-1，則當前最長公共子序列為a0, a1, ..., am-2與b0, b1, ..., bn-2的最長公共子序列與am-1的和。長度為a0, a1, ..., am-2與b0, b1, ..., bn-2的最長公共子序列的長度+1。

（2）如果am-1 != bn-1，則最長公共子序列為max（a0, a1, ..., am-2與b0, b1, ..., bn-1的公共子序列，a0, a1, ..., am-1與b0, b1, ..., bn-2的公共子序列）

如果上述描述用數學公式表示，則引入一個二維數組c[][]，其中c[i][j]記錄X[i]與Y[j]的LCS長度，b[i][j]記錄c[i][j]是通過哪一個子問題的值求得的，即，搜索方向。

這樣我們可以總結出該問題的遞歸形式表達：

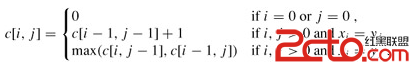
按照動態規劃的思想，對問題的求解，其實就是對子問題自底向上的計算過程。這裡，計算c[i][j]時，c[i-1][j-1]、c[i-1][j]、c[i][j-1]已經計算出來了，這樣，我們可以根據X[i]與Y[j]的取值，按照上面的遞推，求出c[i][j]，同時把路徑記錄在b[i][j]中（路徑只有3中方向：左上、左、上，如下圖）。

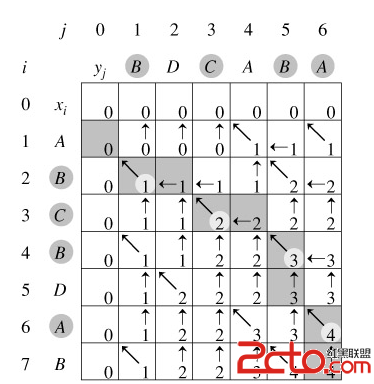
計算c[][]矩陣的時間復雜度是O(m*n)；根據b[][]矩陣尋找最長公共子序列的過程，由於每次調用至少向上或向左移動一步，這樣最多需要（m+n）次就會i = 0或j = 0，也就是算法時間復雜度為O(m+n)。

#include
#include
#include
#include
using namespace std;
int map[10005][10005];
string str1,str2;
int len1,len2;
//最長公共子序列
/***
遞歸解法：
             0                            if(i==0||j==0);
map[i][j] =  map[i-1][j-1]                if(i>0&&j>0&&str1[i]==str2[j])
             max(map[i-1][j],map[i][j-1]) if(i>0&&j>0&&str1[i]!=str2[j])
*/
/*****遞歸超時了！
int LCS(int x,int y)
{
    if(x<0||y<0) return 0;
    if( str1[x]==str2[y])  return LCS(x-1,y-1)+1;
    else  return max(LCS(x-1,y),LCS(x,y-1));

}*/
int main()
{
    while(cin>>str1>>str2)
    {
        len1=str1.length()-1;
        len2=str2.length()-1;

 //       printf(%d
,LCS(len1,len2));
        /***非遞歸解法LCS*/
        for(int i=0;i<=len1+1;i++)
        {
            for(int j=0;j<=len2+1;j++)
            {
                if(i==0||j==0) {map[i][j]=0;continue;}
                if(str1[i-1]==str2[j-1])
                {
                    map[i][j]=map[i-1][j-1]+1;
                }
                else
                {
                    map[i][j]=max(map[i-1][j],map[i][j-1]);
                }
            }
        }
        printf(%d
,map[len1+1][len2+1]);
    }
    return 0;
}

還有一種優化空間的方法，利用滾動數組！這裡也附上代碼。在不需要記錄路徑的時候很好用！

#include
#include
#include
#include
using namespace std;
int map[2][10005];
string str1,str2;
int len1,len2;
//最長公共子序列

int LCS(int x,int y)
{
    for(int i=0;i<=x;i++)
    {
        for(int j=0;j<=y+1;j++)
        {
            if(i==0||j==0) {map[i%2][j]=0;continue;}
            if(str1[i-1]==str2[j-1])
            {
                map[i%2][j]=map[(i-1)%2][j-1]+1;
            }
            else
            {
                map[i%2][j]=max(map[(i-1)%2][j],map[i%2][j-1]);
            }
        }
    }

}
int main()
{
    while(cin>>str1>>str2)
    {
        len1=str1.length();
        len2=str2.length();
        LCS(len1,len2);
        printf(%d
,map[len1%2][len2]);
    }
    return 0;
}